用PLC的反馈变量作为迭代变量计算压缩因子

缪玲梅 李珍华

（华东理工大学工程设计研究院，200237 上海）

1 前言

在工艺、自控、环保、通风等开发研究时，工程中往往需要计算压缩因子，用于实际气体流量的修正。根据维里方程或李-凯斯勒方程计算时涉及到迭代算法，使计算困难。为此，本文介绍将PLC功能块图中的反馈变量作为迭代变量，成功地实现了有关计算。这种计算方法也适用于其他需要进行迭代算法的应用场合。例如，标准孔板的流出系数计算、迭代方程的求解等。

2 PLC功能块图的反馈变量

根据IEC61131-3标准，在功能块图标准编程语言中，引入了反馈变量。标准指出，反馈路径指一个网络的输出参数值返回到同一网络中作为输入参数时，这种连接路径称为反馈路径。相应的变量称为反馈变量。

反馈变量的求值规则如下：

当第一次网络求值时，使用反馈变量的初始值，它可以是该数据类型的约定初始值；用户在变量初始化时规定的初始值；或当具有掉电保持属性的反馈变量在掉电前的数值。

其后，反馈变量的值根据反馈信号确定。即用反馈变量的新值作为该网络的输入。

由此可见，PLC编程语言中的反馈变量具有迭代运算功能。其第一次初始值就是迭代初值，以后将用新的计算结果作为下一次迭代值。

3 维里方程求解压缩因子

对非理想气体，用压缩系数描述其与理想气体之间的偏离程度。即：

对非理想气体，可用维里方程拟合，可用压力或体积作为因子进行拟合。体积拟合公式为：

统计力学指出，第二维里系数B反映两个气体分子间的相互作用对气体p-V-T关系的影响。第三维里系数C反映三个气体分子间的相互作用对气体p-V-T关系的影响等。

上述两个方程有两个未知数Z和V，由于是非线性方程，因此，只能用迭代计算算法求解。即选假设某一变量的初始值，然后，计算其结果，再用该计算结果作为第二次迭代运算的新值，如此循环，直到在该网络中该变量的输入与输出相等。

用PLC的功能块图可方便地实现这种迭代运算。程序如图1所示。

图1 维里方程计算压缩因子的程序

图 中，Temp是 温 度，K；Pressure是 压 力，bar；V是体积，cm3；根据上述工程单位，气体常数Rconst=83.14。B和C是维里系数。例如，根据文献[1]的数据，异丙醇的维里系数为：B=-388 cm3•mol-1，C=-26 000 cm6•mol-2。根据程序，可计算200℃（473.15K）、10bar异丙醇的压缩系数。图中，MUL、DIV和ADD分别是乘、除和加函数[2]。

将程序下装，并运行，得到图2所示运行结果。

由于PLC程序进行不断迭代运算，因此，其运行结果可保证反馈变量输入和输出的数值一致性。运行时需注意，反馈变量V的初始值不能用系统约定的零，因它将造成除以零的出错，实际应用时，可由用户设置一个0～1之间的小值。此外，B和C的数据类型是实数，因此，输入时，应分别是-388.0和-26 000.0。压力数值也用10.0输入。由于温度是热力学温度，因此，应将摄氏温度加273.15转换为开尔文度。

运行结果，在规定的温度和压力下，异丙醇的压缩系数为0.886 615 81，计算精度比文献[1]要高。

4 李-凯斯勒方程求解压缩因子

一般物质都以气、液、固或其混合物存在，具有临界点、三态点、波义耳温度等。物质在临界状态时具有相似性，因此，提出用临界性质作为对比基础的状态方程。

皮策（Pitzer）首先开展以某种物质性质与参考物质性质的偏差为基础的工作，即用偏心因子作为第三参数的压缩因子关联式：

其中，上标(0)表示简单流体，(1)表示参考流体。皮策等用表格形式提供对比温度在0.8～4.0，对比压力在0～9.0的容积和热力学性能之间的关系。

李（Lee B I）和凯斯勒（Kesler M G）改进为采用下列Lee-Kesler（李和凯斯勒）方程，将压缩因子表示为：

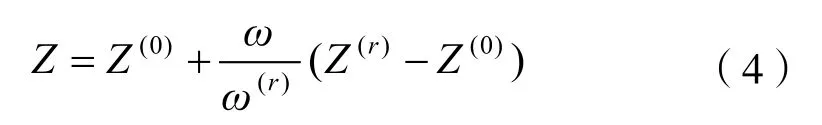
式中：Z(0)— 简单流体（甲烷、氩和氪）的压缩因子，Z(*)— 参考流体（正辛烷）的压缩因子。正辛烷的偏心因子ω(*)=0.397 8。如果，令：

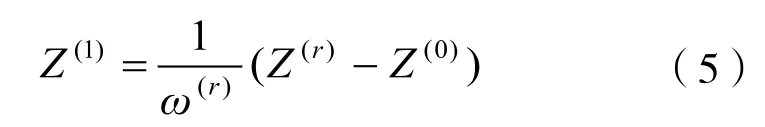
则可得Z=Z(0)+ωZ(1)。

Z(0)和Z(1)可根据维里方程确定。即：

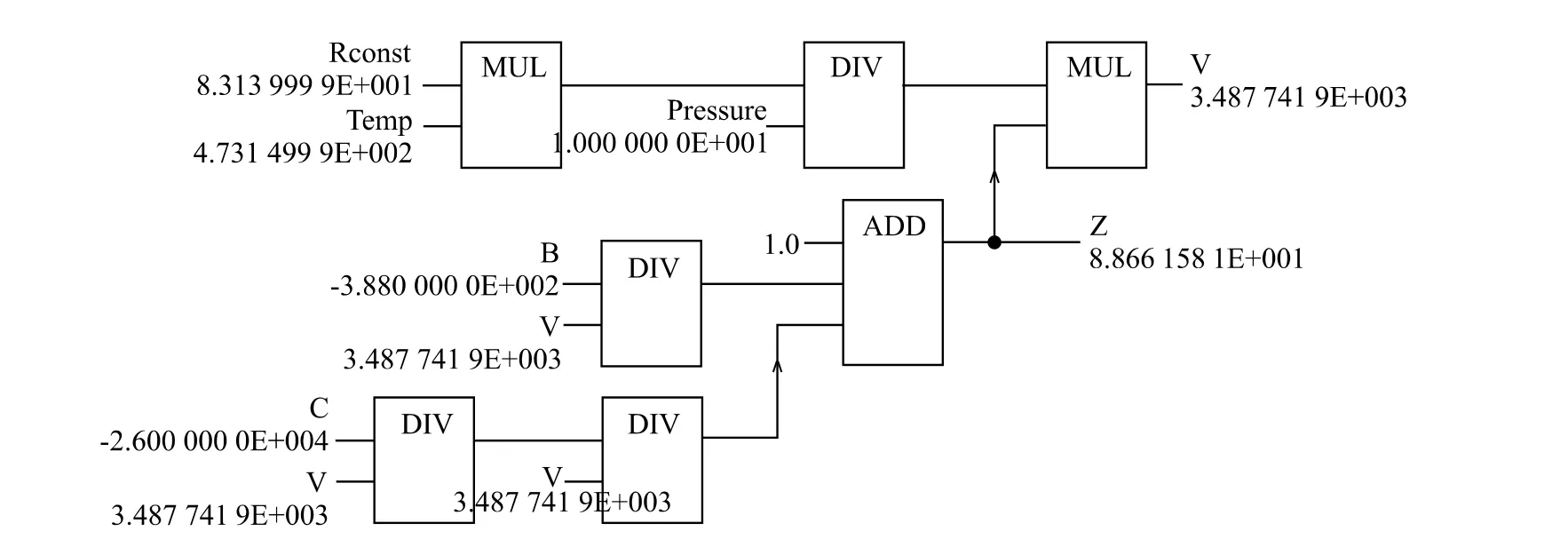
图2 压缩因子计算程序的运行结果

式中的常数见表1。李和凯斯勒方程的实用性评价很高。它适用于气相和液相。类似研究被用于表达其他衍生热力学函数，例如，逸度（f）、焓（H-H°）和熵（S-S°）、来自理想气体状态的等容（Cv-Cv°）和等压（Cp-Cp°）比热容量等。

表1 Lee-Kesler方程中的常数

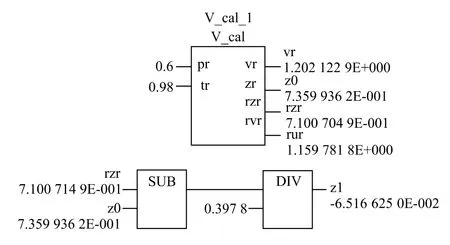
图3 程序运行结果

根据维里方程可确定简单流体和参考流体在对比温度和对比压力下的Zi（i=0，1）。并根据（5）式计算Z(1)。再根据被测流体的偏心因子ω计算出压缩因子Z。

采用PLC编程语言编写了计算Zi的功能块V_cal，其输入变量是pr和tr（标准编程语言对字母的大小写不分），输出变量中，zr即公式中的Z(0)，rzr即公式中的Z(r)。程序调用减法SUB和除法DIV函数，输出变量z1即公式中的Z(1)。最后，调用乘法和加法函数计算压缩因子Z（图中未画出）。图2显示计算程序运行结果。

某被测流体的对比态温度和压力为：pr=0.6、Tr=0.98， 运 算 结 果：Z(0)=0.735 993 62；Z(1)=-0.065 166 250。

5 结束语

用PLC功能块图中的反馈变量可方便地实现迭代算法，用于工程设计中的各种需要迭代运算的计算。例如，本文所介绍的用于压缩因子的计算。也可用于诸如差压式流量计流出系数的计算等计算过程。因此，为迭代运算提供了实施手段。

[1] 施海云. 化工热力学[M]. 上海: 华东理工大学出版社. 2007，80-87.

[2] Smith J M, Van Ness H C, Abbott M M. Introduction to Chemical Engineering Thermodynamics. 7thEdition. 刘洪来等译. 北京: 化学工业出版社. 2008.

[3] 彭瑜, 何衍庆. IEC61131-3编程语言及应用基础[M]. 北京: 机械工业出版社. 2009，46-50.

[4] 何衍庆, 何乙平, 王朋. 常用PLC应用手册[M]. 北京: 国防工业出版社. 2008，190-197.

[5] 王森. 仪表常用数据手册[M]. 北京: 化学工业出版社，1998，180-196.

[6] 中国石化集团上海工程有限公司. 化工工艺设计手册（上）[M].北京: 化学工业出版社，2009，320-324.

[7] 臧福录, 应金良. 石油化工工艺工程师必读（第一册）[M]. 北京：中国石化出版社，1998，67-71.

[8] Chopey N P. Handbook of Chemical Engineering Calculations. 3rd Edition. 朱开宏译. 北京: 中国石化出版社，2005，149-160.