同心环管圆孔射流流动特性的数值模拟

王宗勇， 陈 江， 赵家瑜

(沈阳化工大学能源与动力工程学院，辽宁沈阳 110142)

错流射流也叫弯曲射流，是一种用于流体混合的技术方法，通过一股或多股射流进入到另一流体中，流体之间通过主体扩散、分子扩散和湍流扩散，达到物料混合的目的，适用于多物料、异密度的液-液、气-气及气-液的快速混合体系.

New等［1］采用激光诱导荧光技术(LIF)研究了错流射流椭圆形喷口的涡系和流场的发展，发现导流型椭圆喷口的横向射流具有的射流深度更大.Tian等［2］发展了一套三维LIF系统，并将其应用到未分层和分层横流中的垂向圆浮射流的研究中，实验结果表明，三维系统较其他测量技术能得到更多的实验数据，并能对射流的流动和掺混过程有更深入的理解.Kelso等［3］采用流动热线风速仪和显示技术研究了错流射流圆形喷口的涡系和流场发展，认为逆向旋转涡对(CVP)主导了射流和横流的混合过程.在国内，韩会玲等［4］采用粒子图像测速仪(PIV)对不同射流比时方管横向射流的混合特性进行了研究.李炜等［5］采用粒子图像测速仪(PIV)对错流射流圆形喷口的射流中心轨迹和涡系结构进行了研究.郭婷婷等［6］采用热线风速仪对错流射流圆形喷口的流场进行了研究，得到了射流角度对尾涡发展的影响规律.对于错流射流的流动和涡系发展，存在许多的数值模拟研究报道，分别采用大涡方法［7］，雷诺平均方法［8］和直接数值模拟方法［9-10］对错流射流的流动机理进行了研究.

本文提出一种结构简单的同心套管式错流射流混合器，结构如图1所示.

图1 同心环管射流混合器结构Fig.1 The structure of the jet mixer

横流流体在内管和外管所形成的环形空间内沿轴线方向流动，射流流体通过内管管壁上周向及轴向布置的多个圆孔沿径向垂直射入环形空间，通过与横流流体的碰撞、卷吸等作用实现混合.该混合器中流体流动实际上是受限环形空间内的错流射流，关于该种流动特性的研究较少，对于环形空间错流射流混合过程的认识还不是很透彻.为此，本文采用CFD 中的Fluent［11］软件对单孔、双孔环管错流射流的流动特性进行数值模拟研究，为该种类型混合器的设计及结构优化提供一定的理论依据.

1 数值模型

利用标准 k-ε 湍流模型［7，12-13］计算，其基本方程如下［12］:

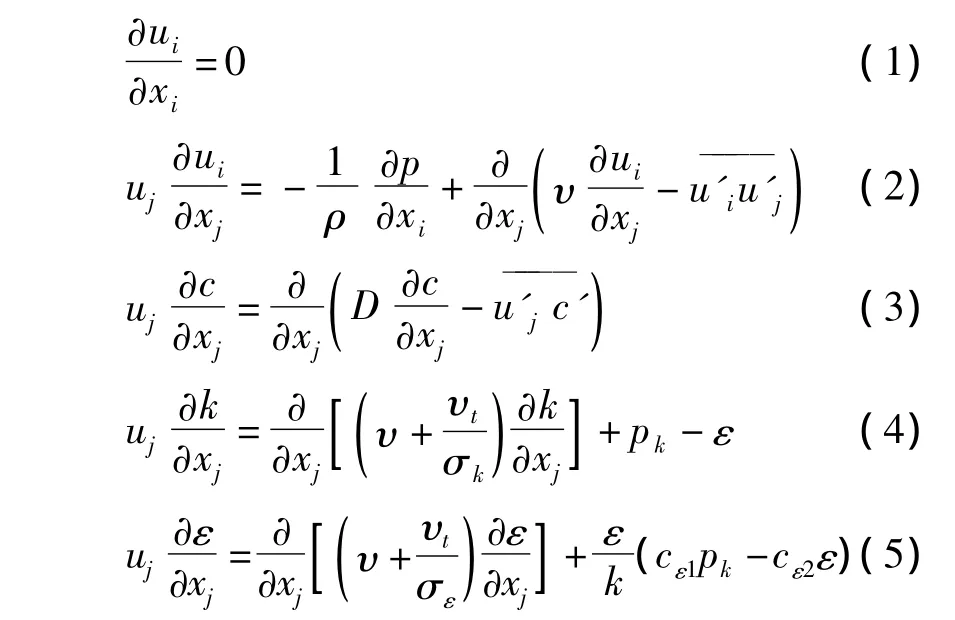
式中:δij为克罗内克尔符号，Sct为斯密特数，其定义为:δij=0(i≠j)或1(i=j);模型常数分别取值为:cμ=0.09，σk=1.00，σε=1.30，cε1=0.44，cε2=1.92.

1.1 建立模型

模型如图2所示，研究的是同心环管，内管上开有1个或2个射流圆孔，分别进行研究，射流孔开孔方向为环管径向即初始射流方向与内外管壁垂直.开2个孔情况下，2个孔位于环管同一周向位置，轴向间距为S.射流喷口直径D=5 mm，管长20D，外管内直径为15D，内管外直径为5D.为便于流动特性的分析，在环管内建立直角坐标系，y轴通过射流孔中心并指向环管半径方向，x轴经过y轴与内管外壁交点并指向横流流动方向，x轴与y轴的交点为坐标原点o，z轴通过原点o垂直于xoy平面，其指向符合右手螺旋定则.第一个射流出口到横流入口的距离为2D，轴向孔间距 S=2D、4D、6D，射流流速比为Rv(射流流速v0与横流流速ua之比).横流流体和射流流体均为水，温度均为298 K，动力黏度为 1.003 mPa·s，密度 998.2 kg/m3.

图2 同心环管结构参数Fig.2 The structure parameter of the concentric annular tubes

1.2 边界条件和网格划分

边界条件为:

(1)横流进口端面(x=-2D):u=ua(ua=0.05、0.1、0.2 m/s)，v=w=0.

(3)管壁处均为固壁，采用壁函数的模拟方式.

(4)射流出口:u=w=0，v=v0(v0=0.1、0.2、0.4 m/s).

模型网格划分，首先在进口端面内管和外管的2个底边上各取120个节点，在进口端面上生成网格，间隔数30，面网格生成后进行体网格的划分.在确保计算结果不受影响的条件下，在计算区域内布置非均匀网格，射流孔上下游2D轴向长度、周向360°范围内网格布置较密，其余部分稍疏，稠密区域网格数为442 800个，稀疏区域网格数为111 600个，如图3所示，这样总共有554 400个网格，并且验证了网格无关性.

图3 计算网格示意图Fig.3 The schematic diagram of computational grid

2 模拟结果与讨论

2.1 单孔射流的流动特性

2.1.1 射流流场

流速比是决定流场特性的一个重要参数［14］，图4、图5给出了射流流体与横流流体在不同流速比Rv下通过射流孔中心的轴截面即xoy平面内的速度等值线图.图4与图5的横流速度相同，均为0.1 m/s(Re=4 976)，而射流速度分别为0.4 m/s(Re=1 990)及0.2 m/s(Re=995).由图4、图5可见:不同的流速比下，横向射流的穿透能力大不相同，随着流速比的增加，其射流穿透深度增大;在受约束的横向射流中射流的发展可分为3个区:中心势流区、最大变形区以及远流场区.中心势流区在射流出口处射流中心，该区域内的射流未受到横流的影响，而在远流场区，射流几乎与横流平行.图6、图7为对应的湍动能图.

横向流动环境中的射流或浮射流实验［15-17］已经观察到存在由一对反向旋转的涡对组成的内部环流在垂直于射流轨迹的平面上.图8(a)～(c)分别给出了Rv=4时，x/D=2、4、6同心环管横截面速度云图.由图8可知横截面上的速度最大值偏离轴对称平面一定的距离.计算结果显示:在射流出口附近，在流速比Rv一定的条件下，射流横截面上速度最大值的偏离程度随着x/D的增加而增加，但增长幅度越来越小，当x/D达到一定值后，射流横断面上速度最大值偏离轴对称平面的距离将基本保持不变，这一现象也说明射流对于横流的周向影响范围随着轴向距离的增加而增大.在进行同心环管射流混合器设计时，靠近轴向后端的射流孔在圆周方向可以设置得相对稀疏一些.

图4 Rv=4轴截面速度等值线图Fig.4 Rv=4 the velocity contour of section

图5 Rv=2轴截面速度等值线图Fig.5 Rv=2 the velocity contour of section

图6 Rv=4轴截面湍动能图Fig.7 Rv=4 the turbulent kinetic energy of section

图7 Rv=2轴截面湍动能图Fig.7 Rv=2 the turbulent kinetic energy of section

图8 Rv=4时横截面速度云图Fig.8 Rv=4 the velocity contour of cross section

2.1.2 射流轨迹线

在进行射流与横流的紊流流动特性研究中，射流轨迹是最重要的特征之一.本文的射流轨迹定义为在通过射流孔中心和环形管道轴线的对称平面内，不同横截面上最大速度中心点的轨迹.图9给出了不同流速比Rv的射流轨迹.由图9可见，射流与横流速度比对射流的穿透深度有很大影响，如在x/D=1时，Rv=1的射流穿透深度y=1.3D;Rv=4的射流穿透深度y=3.5D，后者的射流穿透深度是前者的2.7倍.因此，在射流喷口直径和形状固定的情况下为获得更大的射流穿透深度，必须要提高射流速度比Rv.通过在变量中引入流速比Rv，可将各种射流比的射流轨迹线统一表示成:

该成果与根据理论分析得到的(y/D)∝(x/D)1/3一致，与文献［18］给出的实验成果y/D=(x/D)0.36吻合良好.图 10 给出了射流比Rv=2不变的情况下，同时扩大或缩小射流速度和横流速度时的射流中心轨迹，可以看出射流速度和横流速度成比例增大或缩小对中心轨迹影响很小.

图9 不同射流速度比下的射流中心轨Fig.9 The jet center track of the different jet velocity ratio

图10 同流速比下不同流速的射流中心轨迹Fig.10 The jet center track of the same jet velocity ratio

2.2 双孔射流的流动特性

环管的内管设置多个射流孔可使横流流体与射流流体的接触面积显著增大，同时各射流流动区域流体流动相互影响，若射流孔方位设置合理可进一步改善横流体的混合效果.为此针对轴向双孔之间的流动特性及相互影响做初步探索，关于周向多孔的流动特性尚需进一步研究.

图11为流速比Rv=2、孔间距S=4D时横流中双孔射流中心平面上的速度等值线图.由图11可见，当多孔射流进入横流中时，会形成三个区:未合并区、过渡区和已合并区.在未合并区内，射流的现象与单个射流类似，由于第一个射流对后面射流的遮挡和卷吸作用，后面的射流比前一个射流有更小的弯曲度，从而导出对于相同的射流速度，后一个射流的速度等值线图高度明显高于第一个射流，说明第二射流的射流深度要大于第一个射流;在过渡区，射流与横流之间有强烈的混合，其运动情况比较复杂;在已合并区，射流已完全合并，从而形成一个新的射流.为了分析射流孔间距对流动特性的影响，图12及图13分别显示了流速比Rv=2，孔间距S=2D、6D时的双孔射流中心平面上的速度等值线图.对比图11～图13可以看出，虽然双孔射流的流速比相同，但由于前一射流孔的径向流动区域对后一射流孔的遮挡作用，后一射流孔的流体穿透深度明显增加，这种增加程度随着双孔间距的增大而减少.

图11 S=4D速度等值线图Fig.11 S=4D velocity contour map

图12 S=2D速度等值线图Fig.12 S=2D velocity contour map

图13 S=6D速度等值线图Fig.13 S=6D velocity contour map

3 结论

(1)射流与横流流体的流速比Rv是影响横向射流流场的重要因素，流速比Rv越大，射流的初始动量越大，射流越不容易弯曲，对流场的影响范围也越大.

(2)射流比Rv不变的情况下，射流速度和横流速度成比例增大或缩小对中心轨迹影响很小.

(3)射流存在射流分叉现象，在射流比Rv一定下，在射流的出口附近，射流横截面上速度最大值的偏离随着x/D的增加而增加，但增长幅度越来越小，当x/D达到一定值后，射流横截面上速度最大值与对称面偏离的距离将基本保持不变.

(4)多孔射流由于前一个射流的遮挡作用，后一个射流不容易发生弯曲，穿透深度更大，对流场的影响范围更大.孔间距S影响多孔射流轨迹线，随着孔间距的增大，轨迹线逐渐趋于同一流速比下单孔射流的轨迹线.选择一个合适的射流孔间距可以使两孔的射流轨迹、运动特征较为接近，有利于流体混合.

［1］ New T H，Lim T T，Luo S C.Elliptic Jets in Crossflow［J］.Journal of Fluid Mechanics，2003，494:119-140.

［2］ Tian X，Roberts P J W.A 3D LIF System for Turbulent Buoyant Jet Flows［J］.Experiments in Fluids，2003，35(6):636-647.

［3］ Kelso K R，Lim T T，Perry A E.An Experimental Study of Round Jets in Cross-flow［J］.Journal of Fluid Mechanics，1996，306:111-144.

［4］ 韩会玲，李炜.横流中三维线源型浮力射流特性的研究［J］.水利学报，1999，8(1):46-49.

［5］ 李炜，姜国强，张晓元.横流中圆孔湍射流的旋涡结构［J］.水科学进展，2003，14(5):576-582.

［6］ 郭婷婷，徐忠，李少华.2种角度横向紊动射流的实验分析［J］.西安交通大学学报，2003，37(11):1207-1210.

［7］ 李国能，周昊，杨华，等.横流中湍流射流的数值研究［J］.中国电机工程学报，2007，27(2):87-91.

［8］ 郭婷婷，李少华，徐忠.横向紊动射流的数值与实验研究进展［J］.中国电机工程学报，2003，23(7):191-195.

［9］ Sau A，Sheu T W，Hwang R R，et al.Three-dimensional Simulation of Square Jets in Cross-flow［J］.Phys Rev E Stat Nonlin Soft Matter Phys，2004，69(6):66-71.

［10］ Muppidi S，Mahesh K.Study of Trajectories of Jets in Cross-flow Using Direct Numerical Simulation［J］.Journal of Fluid Mechanics，2005，530:81-100.

［11］孙怀宇，王宇.撞击流反应器的流场测量及数值模拟研究［J］.沈阳化工大学学报，2011，25(3):217-220.

［12］张晓元，李炜，李长城.横流环境中射流的数值研究［J］.水利学报，2002，3(2):32-38.

［13］卞晓静.横流条件下垂直动量射流数值模拟［J］.河海大学学报，2006，34(5):530-533.

［14］李国能，林江，李凯，等.横向射流中心轨迹和扩展宽度［J］.化工学报，2011，62(1):66-70.

［15］ Scorer R S.The Behavior of Chimney Plumes［J］.Int.J.of Air Pollution，1959，1(3):198-220.

［16］ Turner J S.A Comparison Between Buoyant Vortex Ring and Vortex Pairs［J］.J Fluid Mech，1960，7(3):419-432.

［17］ Jirka G H，Fong H L M.Vortex Dynamics and Bifurcation of Buoyant Jets in Cross-flow［J］.J.Eng.Mech.Div.ASCE，1981，107:479-499.

［18］ Kamotani Y，Greber I.Experiments on a Turbulent Jet in a Cross Flow［J］.AIAA Journal，1972，10(11):1425-1429.