基于FARIMA-GARCH模型的网络业务预测算法

杨双懋，郭伟，唐伟

(1. 电子信息控制重点实验室，四川 成都 610036；2. 电子科技大学 通信抗干扰技术国家级重点实验室, 四川 成都 611731）

1 引言

网络业务的流量特性是进行网络协议设计、性能评估、资源管理和设备研究所必须考虑的重要因素，目前已经有大量文献对此做出了研究。早期对网络业务的流量特性的研究以泊松模型为主。然而，通过对真实网络流量的深入分析发现数据交换网络的流量特征不能通过泊松模型描述[1]。特别是文献[2～4]通过对局域网和广域网的流量特性进行了实际测量与分析，发现了网络流量具有自相似(self-similarity)和长相关性(long-range dependence)。因此，传统的描述短相关性(short-range dependence)的泊松过程、Markov过程、AR(autoregressive)、MA(moving average)、ARMA(autoregressive moving average)和ARIMA(autoregressive integrated moving average)过程等已不适合于描述 LRD业务流。同时，长相关模型又缺乏刻画业务短相关性的能力，因此必须采用能同时描述LRD和SRD的数学模型。当前网络流量的建模和预测主要集中于采用时间序列模型的算法[5]、小波模型[6～8]以及神经网络模型[9～16]等。

经典的 ARMA模型的预测算法[17]具有较低复杂度，但是不适合于描述 LRD业务流；基于分数自回归求和滑动平均(FARIMA, fractional autoregressive integrated moving average)模型的预测算法[18]相对于文献[17]提高了预测精度，但是对于网络业务的剧烈波动性也不太适应。文献[6～8]把小波分析和时间序列模型结合起来，通过时间序列模型预测小波的细节分量或者预测重构后单支分量，再进行总体流量重构，但没有给出如何进行长期预测和区间预测的方法。

基于神经网络的预测模型可以对非线性的序列进行预测，能较好地描述网络流量的不稳定性，但训练复杂度和计算复杂度都较高。BP(back propagation)神经网络采用全局逼近，其训练时间偏长，因此其应用受到限制；而径向基(RBF, radial basis function)神经网络采用局部逼近训练算法，能够以任意精度逼近任意连续函数。文献[15]把RBF神经网络应用到网络业务预测算法中，文献[16]用RBF神经网络对流量的小波细节分量进行预测，再将流量进行重构，但是没有考虑业务的长相关性，同时也没有给出如何确定神经网络的嵌入维数和延迟时间。这2个参数将在很大程度上决定预测算法的精度[19]，然而目前还没有普适的方法进行确定[19,20]。

经典的基于 FARIMA 模型的预测算法[18]分为序列零均值化、分数差分阶数估计、序列建模和预测3个关键步骤。其序列零均值化采用了整体去均值法，但是该法无法降低序列的波动性；而采用传统的估计算法[5]得到的分数差分阶数依然不够精确。同时，FARIMA模型本身不能对序列的波动性进行有效跟踪。作者在前期研究中提出了一种基于 FARIMA改进的预测算法[21]，而本文将作进一步扩充，提出一种基于广义自回归条件异方差(FARIMA-GARCH,generalized autoregressive conditional heteroscedasticity)模型的网络业务预测算法。

本文所提算法流程如图1所示。首先，提出一种分段双向CUSUM检测算法将序列零均值化，以此减小序列的波动性；然后针对分数差分阶数的精确估计提出了一种限定搜索法；接着对序列进行FARIMA-GARCH建模；最后进行流量预测和区间估计。

2 基于FARIMA-GARCH模型的预测算法

2.1 FARIMA-GARCH模型

时间序列中的 FARIMA(p,d,q)-GARCH(r,s)模型[22]是将FARIMA与GARCH相结合，能同时描述网络业务的长相关性、短相关性和波动性的离散时间序列模型。令tX表示业务的时间序列，则该模型可以表示为

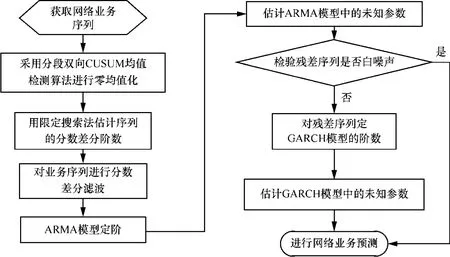
图1 网络业务建模预测流程

其中，B是时延算子，即 B Xt= Xt-1。分数差分阶数 d ∈(-0 .5,0.5)， ∇d为分数差分算子。Φ(B)、Θ(B)、Ω(B)和A(B)为复变量多项式[18,22]。非负整数p和q是FARIMA模型的自回归阶数和滑动平均阶数，{at}表示业务序列Xt的残差序列，表示条件方差，非负整数r和s表示GARCH模型的阶数，{vt}为零均值且方差为1的高斯白噪声。

当 d = 0 时， Xt退化成ARMA(p, q)，只呈现出短相关性。所以，本文将在精确估计出分数差分阶数d后，通过分数差分来消弱序列中的长相关性，以利用经典的时间序列理论进行参数估计。

2.2 分段双向CUSUM均值检测算法

式(2)中要求输入的序列必须是零均值平稳序列，实际的用户业务序列往往不满足零均值的要求。传统的去均值的方法是整体去均值法[18]，但是该法不能减小序列的方差；而分段去均值法能够得到更小的方差。因此，本文采用分段去均值法对序列进行零均值化，且有定理1成立。

定理 1 分段去均值法获得的方差不大于整体去均值法。

证明 设序列 { yt} ：y1, y2, … ,yv, yv+1,yv+2,… ,yL是具有均值变化点的时间序列，其均值为μ3，其中，时间点v为变点；设序列 y1, y2,… ,yv满足均值为μ1，方差为，长度为v；后半部分序列yv+1,yv+2,… ,yL满足均值为μ2，方差为，长度为L - v ，且有 μ1≠μ2。按照分段去均值法去均值后，得到时间序列{γt}；按照整体去均值法，得到{πt}，表示为

又由条件 μ1≠ μ2，可得D(πt)＞D(γt)。

由于网络业务呈现出波动率聚类特性，即在较大幅度波动后面伴随着较大幅度的波动，在较小波动幅度后面紧接着较小幅度的波动。为了更好地检测序列均值的变化和在建模时平滑业务序列的波动性，本文提出一种分段双向 CUSUM(cumulative sum)均值检测算法。图2是均值检测算法的窗口移动示意，检测窗口中包含L个业务序列样本值。图2(a)是窗口未检测出序列均值的变化的示意，此时窗口右移一个样本点，然后继续检测新窗口中的样本。图2(b)在窗口中检测到时间点为 tC的均值变化点，此时窗口右移 C -1个样本点再继续检测。

图2 均值检测数据窗口示意

给定检测门限eh、序列的期望修正值δ、窗口起始值和长度L。记当前窗口起始时刻为1t，向上变化决策函数为，向下变化决策函数为

其中，Y+运算含义是：当 0Y＞ 时，Y Y+= ；当 Y≤0时， 0Y+= 。Y-运算含义是：当Y≤0时，Y Y-= ，当 0Y＞ 时， 0Y-= 。于是，分段双向 CUSUM均值检测算法步骤可由图3的伪代码表示。

图3 分段双向CUSUM算法伪代码

由于CUSUM检测算法假设序列的均值为负，而本算法的目标检测序列在实际物理系统中都是非负序列，因此需要修正值δ来改造时间序列，取为E(Xt)。而检测门限值eh采用3倍标准差法，即eh = 3 × s td( Xt)。期望修正值δ、检测门限值eh和窗口长度L可以根据当前业务特征、精度和灵敏度要求在实际运用中灵活调整。

2.3 限定搜索法

为了获得流量的分数差分阶数 d，可以通过估计序列的Hurst指数，再由关系式 0.5H d= + 得到。经典的 Hurst指数估计方法[5,23～27]的时间复杂度不尽相同，但对实际的复杂网络流量，这些方法的准确度都不高。由于Hurst指数描述了序列整体平均的自相似特性，而这种整体的特性不一定适用于具有时变性的复杂网络流量，因此对真实流量序列进行估计时上述方法都存在误差，采用不同方法对同一序列获得的Hurst指数也有所不同[28]。因此，本文将计算复杂度比较低的 A-V小波法[26]和搜索法相结合，提出一种限定搜索法对d进行精确估计。

如图4所示，限定搜索法先使用A-V小波法估计出分数差分阶数d的粗估计ˆd，然后在ˆd的邻域内按照一定的规律遍历，用ˆd对序列进行分数差分滤波，计算滤波后序列的自相关函数的平方和[29]。将平方和达到最小的ˆd作为分数差分参数d。

图4 限定搜索法

对流量序列 Xt进行分数差分滤波后获得长度为N的序列 Wt，即设 W 的K点协方差t函数估计量，归一化自相关函数估计量k)和自相关函数序列的平方和M用如下公式计算

给定d的邻域大小ed、M的精度ef，搜索步长step取为 /2ed 。用A-V小波分析法估计当前序列的粗估计值，则当前搜索点dc取为ed-。于是，限定搜索法的步骤可图5的伪代码所表示。

图5 限定搜索法法伪代码

其中，M(dc)表示对序列tX进行分数差分滤波后，再用式(4)～式(6)获得滤波后序列的平方和M。

对于精度K，可以根据序列的自相关函数估计量是否显著趋于0决定。精度需求ed和ef可以根据数据量和最终精度要求在实际运用中灵活调整。

2.4 模型参数估计和检验

如图1所示，在前面的2个步骤之后，需要进行模型的参数估计和检验，主要包括模型定阶、估计参数和拟合检验3个步骤。本文采用了时间序列中的经典方法[30,31]进行处理。

2.5 业务序列预测算法

基于上述分析，提出如下算法实现图1的流程。

1) 对给定业务流依2.2节中分段双向CUSUM均值检测算法进行去均值，得到零均值序列tX。

2) 采用 2.3节中限定搜索法得到序列tX的分数差分阶数d。

3) 对tX进行分数差分滤波，得到ARMA序列tW。

4) 利用AIC(akaike information criterion)准则[32,33]对序列tW定阶。

5) 得到序列 Wt的参数组，利用式(1)迭代获得残差序列｛at｝ 。

6) 检测｛at｝ 是否为白噪声，如果是，则建模算法停止，转入步骤9)；否则，则进入一下步骤。

7) 利用AIC准则对｛at｝ 进行GARCH(r,s)定阶。

8) 估计得到 GARCH(r,s)模型的参数组，利用式(3)迭代计算出异方差序列{}。

9) 进行业务序列的预报。

为了减小预测误差，需要对预测值进行均值补偿。设从时间点t后的 Wt的1步预测值( 1)为

表1 不同方法对自相似序列Hurst指数估计结果

利用2.2节中的方法，对时刻 t - L + 1→ t的长度为L的序列进行均值检测，如果没有检测到变点，则按照式(7)获得序列 Xt的单步预测值(1)，若检测到变点为 tC，则按照式(8)获得序列 Xt的单步预测值(1)

3 预测算法的性能分析

3.1 算法的复杂度分析

假定业务序列 Xt的长度为N，预测过程的时间复杂度分析如下。在限定搜索法中需要 O ( N)次运算获得d的粗估计值，而精估计至少需要O ( -log(e f) K N)次运算，相比较于K， - l og(e f)很小，因此认为限定搜索法的运算次数为 O ( K N )。

其他步骤的运算时间和传统的 FARIMA算法相当，需要 O ( N2)次运算来进行模型定阶和参数估计。由于K相较于N通常较小，因此整个预测算法并没有显著地增加运算的耗时。

3.2 实验分析

为了在统一的评价体系下评估限定搜索法，采用Hosking[34,35]法生成若干不同Hurst指数的数据序列，用来检测算法的性能。选择方差法、R/S分析法、A-V小波法以及自适应法[27]进行比较。数据序列都采用4 096点，运行20次取平均值。

表1给出了对自相似业务序列进行Hurst指数估计的结果，同时还给出了相应算法在仿真平台上的耗时。当 Hurst指数较小时，5种方法估计结果的精度相差不大；当Hurst指数较大时，方差法和R/S分析法的精度较差，误差达到了10%，对后续建模算法的准确度影响较大。R/S分析法耗时最高，是A-V小波法耗时的数百倍，这与R/S分析法具有所有算法中最高的时间复杂度 O ( N2)相应。

虽然小波法和自适应法耗时最短，估计误差在3%～5%左右，但经常出现无法有效而准确地确定最优尺度区间的现象。在面临不同实际业务流时，2种算法都没有给出最优尺度区间的选择方法。

限定搜索法建立在小波法和检测序列自相关函数平方和的基础上，估计误差大致为 1‰，时间复杂度为 ( )O KN。该算法在增加少量计算开销的代价下，提供了更优的性能，能够提高后续建模精度。

采用均方根误差(RMSE, root mean-square err or)和相对均方根误差(RRMSE, relative root meansquare error)来衡量预测的效果，定义如下。

使用GARCH模型对｛at｝ 建模的目的是提高区间预报的准确性，因此需要定义一个统计量来描述区间预报的准确度。可以依序列观测值是否落入当前观测值预测区间获得一个 1-0值的命中序列｛ht｝ 。设检测的总次数是T，记某个序列观测值Xt( k)的95%的置信区间是 Δt( k )，有

其中，置信区间针对不同模型具有不同的表达式。定义区间预测准确度(IFA, interval forecasting accuracy)为

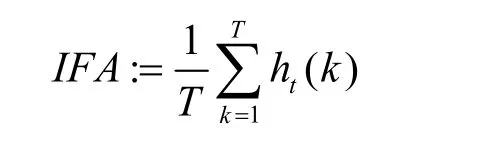
仿真实验中采用来自ACM SIGCOMM’04会议的真实网络流[35]。用 sig04_ver01(如表 2所示)代表从SIGCOMM’04数据流中随机选出的10 000个连续的分组到达时间戳。类似地，sig04_ver02和sig04_ver03分别代表了另外2组分组到达时间戳。

表2 仿真业务参数

为了考察大时间尺度和小时间尺度下预测算法的性能，将这3组数据按照10ms(小时间尺度)和100ms(大时间尺度)的尺度进行聚合，聚合后的序列样本值代表当前时间尺度内到达的分组个数，得到表2中的6条业务序列。然后将业务序列分为前后2部分，前部占总长的80%，用于模型辨识和参数估计，最后用建立好的模型对未来值进行预测，将预测值和后部的真实值进行比较和分析。

在RBF预测算法的仿真中，由于无法确定时间序列的最佳嵌入维数和延迟时间[19,20]，因此延迟时间取 1。嵌入维数采用多次训练的方法来确定，将预测效果最好的神经网络作为RBF算法预测网络，同时限制最大神经元个数是1 500。

表3～表5分别对比了在小时间尺度下几种算法的预测性能。其中，RMSE越小说明预测值偏离真实值的幅度越小，预测精度越高。从结果看出，本文算法的RMSE在单步预测的条件下小于FARIMA预测算法，和RBF算法基本相当，在预测步数明显增加的情况下，本文算法明显占优。

RRMSE是归一化的RMSE指标，衡量了预测值与真实值之间归一化的偏离程度。从结果看出，本文算法的RRMSE在单步预测条件下是最优的。在预测步数增加时，本文算法和RBF算法的小幅增加，而FARIMA算法的RRMSE快速增加到不合理的状态，例如表5中FARIMA算法的RRMSE快速增加到 7，此时预测值的误差已经大致相当于真实值的7倍左右，预测性能已经很不可靠。

表3 小时间尺度下预测业务流sig04_ver01的性能评价

表4 小时间尺度下预测业务流sig04_ver02的性能评价

表5 小时间尺度下预测业务流sig04_ver03的性能评价

IFA指标衡量了预测算法的区间估计性能，由于RBF算法没有实现区间估计的方式，因此只对比了 FARIMA算法。在仿真中采用置信度为95%的置信区间，因此平均来看，IFA不应小于95%。但从结果来看，当预测步数大于 1步的时候，FARIMA算法的IFA下降到50%～60%左右，这说明一半以上的真实值落在了预测区间的外面，预测性能较差。而由于GARCH模型能比较精确和快速地跟踪方差变化，根据历史值来调整预测区间的大小，使得真实值落入预测区间的概率大大提高，IFA都在75%以上。在表4中，IFA基本稳定在95%左右。

表6～表8分别对比了在大时间尺度下几种预测算法的性能。由于大时间尺度下时间序列的突发性要相对小一些，3种算法的性能都相对小时间尺度下有所提高，说明预测大时间尺度网络流量要比预测小时间尺度的网络流量更加可靠和可实现。例如大时间尺度下的IFA，对比表3和表6，表4和表7、表5和表 8，同样条件下IFA的性能优于小时间尺度，这说明大时间尺度下的业务流由于方差更大，方差波动程度也更剧烈，GARCH模型能有效捕捉到这种波动性，因此根据GARCH估计出的区间能够以更高的概率覆盖真实值，达到较好的预测性能。

表6 大时间尺度下预测业务流sig04_ver01的性能评价

表7 大时间尺度下预测业务流sig04_ver02的性能评价

表8 大时间尺度下预测业务流sig04_ver03的性能评价

同时从仿真结果中看出，随着预测步数的增加，RMSE和RRMSE都出现增加。本文算法增加的趋势要平滑一些，而FARIMA算法增加幅度在有些业务流上则快速和明显。而随着步数的增加，IFA在有些业务流上也出现比较明显的大幅下滑，说明该流量序列是一个随机性和突发性都特别强的时间序列，不太可能进行长期地精确预报，因此在做出短期预报后，需要及时根据后续真实值修正模型，再继续预报。仿真结果表明，单步预测的性能是比较可靠和精确的。

图6是业务流sig04_ver02在小时间尺度下的一段预测结果，采用单步预测。小时间尺度上网络流量具有很强的突发性，单峰式的流量暴增点随处可见。FARIMA模型采用同方差假定，不能有效跟踪这种突发性的流量增加点。因此在这些流量突发处，FARIMA模型预测值与真实值差距较大。而RBF算法同样不能有效预测这些突发点，更多是跟踪序列均值的变化。本文算法能先平滑序列波动，再使用GARCH跟踪序列的波动性，使得这些突发点处的预测值比较接近真实值，预测效果较好。

图6 小时间尺度流量预测仿真结果

图7是业务流sig04_ver01在大时间尺度下的一段预测结果。由于时间尺度的加大，在一定程度上平滑了序列的突发性，因此流量暴增点的个数明显减少，但是依然存在个别单峰式突发点。从仿真结果看出，在流量比较平稳的阶段，3种算法预测结果都能有效地逼近真实值。不过与图6类似，在单峰式突发点，FARIMA模型发现了流量突发，而不能较准确地捕捉到突发点的流量，RBF算法只能预测到序列均值附近，而基于FARIMA-GARCH的预测算法明显更能有效预测突发点的流量。

图7 大时间尺度流量预测仿真结果

4 结束语

本文首先对流量预测中的2个关键步骤进行改进，即提出了分段双向CUSUM检测算法和限定搜索法，然后在此基础上提出一种基于 FARIMAGARCH模型的网络业务预测算法。

仿真实验验证了限定搜索法的性能，在 Hurst指数较大情况下，其精度高于方差法和R/S分析法。虽然比A-V小波法增加了少量的计算量，但是估计误差也相应减小，并且该算法的时间复杂度依然维持在 ( )O KN ，该复杂度与A-V小波法基本相当。

接着采用真实网络的业务流量对基于 FARIMAGARCH预测算法进行了仿真验证。本文算法的RMSE和RRMSE与RBF算法基本相当，而优于传统的FARIMA预测算法。同时对突发点的跟踪和预测能力明显优于对比算法，其区间估计的性能也较传统的FARIMA预测算法要好。本文算法在保持与FARIMA预测算法基本等价的运算时间复杂度下，提供了更好的均值和区间估计性能，可以方便地应用于网络流量预测、接入控制、带宽预留和分配以及负载均衡等场合。

[1] PAXSON V, FLOYD S. Wide-area traffic： the failure of poisson modeling[J]. IEEE/ACM Transactions on Networking, 1995, 3(3)：226-244.

[2] LELAND W E, WILLINGER W, TAQQU M S, et al. On the selfsimilar nature of ethernet traffic[J]. Computer Communication Review,1995, 25(1)：202-213.

[3] LELAND W E, WILLINGER W, TAQQU M S, et al. On the selfsimilar nature of ethernet traffic(extended version)[J]. IEEE/ ACM Transactions on Networking, 1994,2(1)：1-15.

[4] WILLINGER W. Self-similarity in wide-area network traffic[A].Lasers and Electro-Optics Society Annual Meeting[C]. San Francisco,USA,1997.462-463.

[5] HAMILTON J D. Time-Series Analysis[M]. New Jersey： Princeton University Press, 1994.

[6] 王西锋, 高岭, 张晓孪. 基于小波技术的网络流量分析和预测[J].计算机应用与软件,2008,25(8)：70-72.WANG X F, GAO L, ZHANG X L. A network traffic analysis and forecast based on wavelet technology[J]. Computer Applications and Software, 2008, 25(8)：70-72.

[7] 白翔字,叶新铭,蒋海. 基于小波变换与自回归模型的网络流量预测[J].计算机科学,2007,34(7)：47-49.BAI X Y, YE X M, JIANG H. Network traffic predicting based on wavelet transform and autoregressive model[J]. Computer Science,2007,34(7)：47-49.

[8] 陈晓天,刘静娴. 改进的基于小波变换和FARIMA模型的网络流量预测算法[J].通信学报,2011,32(4)：153-157.CHEN X T, LIU J X. Network traffic prediction based on wavelet transformation and FARIIMA[J]. Journal on Communications, 2011,32(4)：153-157.

[9] TARRAF A, HABIB W, AHMED A. ATM multimedia traffic prediction using neural networks[A]. Global Data Networking Proceedings[C]. Cairo, Egypt, 1993.77-84.

[10] WANG F, XIA H B. Network traffic prediction based on grey neural network integrated model[A]. International Conference on Computer Science and Software Engineering[C]. Wuhan, China, 2008.915-918.

[11] JUN L, LI T, LI X. Network traffic prediction algorithm and its practical application in real network[A]. IFIP International Conference on Network and Parallel Computing Workshops[C]. Liaoning, China,2007.512-517.

[12] ARDHAN S, SATSRI S, CHUTCHAVONG V, et al. Improved model for traffic fluctuation prediction by neural network[A]. International Conference on Control, Automation and Systems[C]. Seoul, Korea,2007.122-125.

[13] ZHU L, QIN L, XUE K, et al. A novel BP neural network model for traffic prediction of next generation network[A]. Fifth International Conference on Natural Computation[C].Tianjin, China, 2009.32-38.

[14] LI X Y. Prediction of traffic flow base on neural network[A]. Intelligent Computation Technology and Automation[C].Changsha, China,2009.374-377.

[15] 王俊松,高志伟. 基于RBF神经网络的网络流量建模及预测[J].计算机工程与应用,2008,44(13)：6-11.WANG J S, GAO Z W. Network traffic modeling and prediction based on RBF neural network[J]. Computer Engineering and Applications,2008,44(13)：6-11.

[16] WEN Y, YANG D Y, ZHAO Y L. Traffic flow prediction based on wavelet transform and radial basis function network[A]. International Conference on Logistics Systems and Intelligent Management[C].Harbin, China, 2010.969-972.

[17] 邹伯贤,刘强. 基于 ARMA 模型的网络流量预测[J].计算机研究与发展, 2002, 39(12)：1645-1652.ZOU B X, LIU Q. Arma-based traffic prediction and overload detection of network[J]. Journal of Computer Research and Development,2002, 39(12)：1645-1652.

[18] 舒炎泰,王雷,张连芳等. 基于FARIMA 模型的Internet网络业务预报[J].计算机学报,2001,24(1)：46-54.SHU Y T, WANG L, ZHANG L F, et al. Internet traffic modeling and prediction using FARIMA models[J]. Chinese Journal of Computers,2001, 24(1)：46-54.

[19] 冯慧芳. IEEE 802.11 无线局域网业务流特性研究及预报[D].天津：天津大学,2006.FENG H F. Traffic Characterization and Prediction in IEEE 802.11 WLANs[D]. Tianjin： Tianjin University,2006.

[20] 吕金虎.混沌时间序列分析及其应用[M]. 武汉：武汉大学出版社,2002.LV J H. Chaos Time Series Analysis and Application[M].Wuhan： Wuhan University Press, 2002

[21] 杨双懋,郭伟,唐伟.认知无线网络中基于时间序列预测的冲突分解算法.通信学报,2011,32(11)：51-58.YANG S M, GUO W ,TANG W. A collision resolution algorithm based on time-series forecasting for cognitive wireless networks[J].Journal on Communications, 2011,32(11)：51-58.

[22] WILFREDO P. Long-Memory Time Series ： Theory and Methods[M].Hoboken： John Wiley & Sons, 2007.

[23] ZHANG H F, SHU Y T, YANG O. Estimation of hurst parameter by variance time plots[A]. IEEE Pacific Rim Conference on Communications, Computers and Signal Processing[C]. Victoria, Canada, 1997.883-886.

[24] CLEGG R G. A practical guide to measuring the hurst parameter[J].International Journal of Simulation： Systems, Science and Technology,2006,7(2)：3-14.

[25] LAU W C, ERRAMILLI A, WANG J L, et al. Self-similar traffic parameter estimation： a semi-parametric periodogram-based algorithm[A]. IEEE Global Telecommunications Conference[C]. Singapore, 1995.2225-2231.

[26] ABRY P, VEITCH D. Wavelet analysis of long range dependent traffic[J]. IEEE Transactions on Information Theory, 1998, 44(1)：2-15.

[27] 洪飞,吴志美. 基于小波的 Hurst指数自适应估计方法[J]. 软件学报,2005,16(9)：1685-1689.HONG F; WU Z M. Adaptive hurst index estimator based on wavelet[J]. Journal of Software, 2005, 16(9)：1685-1689.

[28] WILLIAM R, LES O, MARCO R, et al. Estimators for long range dependence： an empirical study[J]. Electronic Journal of Statistics,2009.1-16.

[29] 陈彦辉,谢维信. 随机分形信号参数的分数差分估计[J].电子与信息学报,2001,23(1)：9-15.CHEN Y H, XIE W X. Fractional difference estimation for the parameters of random fractal signal[J]. Journal of Electronics and Information Technology, 2001, 23(1)：9-15.

[30] BROCKWELL P J,DAVIS R A. Time Series： Theory and Methods[M].New York： Springer,1987.

[31] GARCH 模型与应用简介[EB/OL]. http：//wenku.baidu.com/view/bd93f636a32d7375a41780b7.html, 2011.GARCH model application profile[EB/OL]. http：//wenku.baidu.com/view/bd93f636a32d7375a41780b7.html, 2011.

[32] AKAIKE H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974,19(6)：716-723.

[33] SHIBATA R. Selection of the order of an autoregressive model by Akaike's information criterion[J]. Biometrika, 1976,63(1)：117-126.

[34] HOSKING J R M. Modeling persistence in hydrological time series using fractional differencing[J]. Water Resources Research, 1984,20(12)： 1898-1908.

[35] Sigcomm 2004 trace dataset[EB/OL]. http：//www.crawdad.org/meta.php?name=uw/sigcomm2004, 2011.