有限采样影响下秩减估计器的波达方向估计性能分析

王鼎，姚晖，吴瑛

（解放军信息工程大学 信息系统工程学院，河南 郑州450002）

1 引言

众所周知，阵列误差自校正方法需要将信源波达方向(DOA, direction-of-arrival)和阵列误差参数根据某种准则进行联合估计或联合优化[1～3]，其中联合估计所涉及到的高维、多模非线性优化问题往往会带来庞大的运算量，从而使得算法的实时性和顽健性较差，全局收敛性也难以得到保证。为了克服阵列误差自校正方法中存在上述问题，一类所谓“秩减估计器(RARE, rank reduction estimator)[4～16]”引起了国内外学者的广泛关注，其主要优势在于能够实现阵列误差参数和信源方位的联合且“去耦合”估计，可避免迭代运算和局部收敛等问题。例如，文献[4,5]分别针对均匀线阵和均匀圆阵互耦矩阵的特殊结构(Toeplitz结构)，提出了互耦自校正RARE；文献[6～11]分别针对L字型阵、Y字型阵、十字型阵、均匀六边形阵和圆环阵的互耦矩阵特性，提出了相应的互耦自校正 RARE；文献[12]提出了累量域互耦自校正 RARE；文献[13]利用精确校正的辅助阵元提出了一种可用于校正“方位依赖”幅相误差的RARE，该方法也称为辅助阵元法(ISM，instrumental sensors method)；文献[14,15]提出了多子阵部分阵列误差的自校正RARE，其中的阵列误差包括子阵与子阵之间的阵元位置误差或幅相误差等；文献[16]则提出了多子阵互耦自校正RARE等。上述一系列RARE都能够在一定条件下取得较好的效果，并且能够有效避免阵列误差自校正方法中的一些缺点。

根据文献[4～16]中的讨论可知，RARE可以看成是 MUSIC算法[17]的一种推广，或者说 MUSIC算法是RARE在没有阵列误差条件下的一种特殊形式。由于MUSIC算法是一种最为重要的DOA估计算法，所以关于其方位估计性能的理论研究报道相对较多，例如，文献[18,19]利用一阶误差分析方法推导了有限采样影响下MUSIC算法的方位估计均方误差；文献[20,21]利用二阶误差分析方法推导了有限采样影响下MUSIC算法的方位估计偏置等。由于RARE是MUSIC算法的一种推广，鉴于其在阵列误差自校正方法中的重要性，笔者已在文献[22～24]中从不同方面推导了其性能，其中包括未预期模型误差影响下 RARE的角度分辨性能[22]和DOA估计性能[23]，以及有限采样影响下RARE的角度分辨性能[24]。为了保证研究工作的系统性和完整性，本文将从理论上分析有限采样影响下RARE的DOA估计性能。与文献[22～24]中的分析方法不同的是，本文将基于文献[25]给出的信号(或噪声)子空间正交投影矩阵的扰动定理，分别推导了RARE的方位估计均方误差、偏置以及测向成功概率的理论表达式，并针对文献[4,5]中的均匀阵列互耦自校正RARE和文献[13]中的辅助阵元法给出数值实验。

在讨论主题前，这里先给出一些文中常用符号的定义：1)⊗表示矩阵的Kronecker积；2)vec(·)表示矩阵向量化算子；3) Nn(μ, C )表示均值(向量)为μ，方差(矩阵)为C的n维高斯分布，χ2(n,δ)表示自由度为n，非中心参数为δ的卡方分布；4)向量(或标量)x˙(θ)、x˙(θ)和 ˙x˙(θ)分别表示向量(或标量)x(θ)对θ求一阶、二阶和三阶导数；5)o(ε)表示ε的高阶无穷小，而 O (ε)表示ε的等价无穷小。

2 预备数学知识

为了描述文中理论推导，本节将引出若干预备命题，它们对于文中的理论分析起着重要的作用。

引理1[26]设实随机变量 x ～ χ2(n,δ)，则其特征函数为

引理1的证明见文献[26]。

命题 1 设n维实随机向量 x ～ Nn( μ, In)，令A ∈ Rn×n为对称矩阵，并且满足rank[A] =m，假设A的m个非零特征值分别为 ρ1, ρ2,… ,ρm，相应的单位正交特征向量分别为 e1, e2,… ,em，则高斯随机向量二次型 y =xTAx的特征函数为

命题1的证明见附录A。

命题2的证明见附录B。

进一步可得

命题3的证明见附录C。

3 阵列信号模型和秩减估计器简介

假设某阵列含有M个阵元，现在阵列远场处有D个非相干的窄带信源以平面波的方式入射，则阵列的输出响应为

其中，T（θ）∈CM×K表示仅与方位θ有关的矩阵函数，这里将其按列分块表示为 T （θ）=，而表示包含阵列误差参数η的列向量。

根据式(7)可知阵列协方差阵为

其中， R0=BPBH为无噪条件下的阵列协方差阵，为信源协方差阵(当信源统计独立时，是对角矩阵；当信源统计相关但不相干时，是正定矩阵)，σ2表示噪声功率。现对矩阵R进行特征分解，其特征值按照由大到小的顺序可假设为[17]

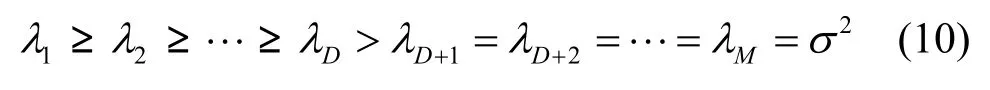
若令上述D个大特征值对应的单位正交特征向量分别为 u1,u2,… ,uD，并记 U = [ u1u2…uD]，则理想条件下信号子空间和噪声子空间的正交投影矩阵分别为 Π = UUH和 Π⊥= IM-UUH，相应地RARE 空域谱为[4～16, 22～24]

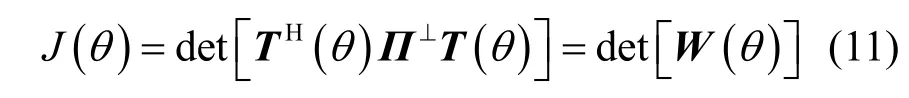
其中， W （θ ） = TH（θ） Π⊥T （ θ） ∈ CK×K。在参数满足一定条件下[4～16]，信源方位可由下式精确获得[4～16,22～24]

在实际计算中，由式(9)确定的理想协方差阵是无法得到的，只能通过有限采样获得它的一致(最大似然)估计值，其中N为样本点数。若对Rˆ进行特征分解，则仍可得到D个较大特征值，假设它们对应的单位正交特征向量分别为，并记，则有限采样影响下信号子空间和噪声子空间的正交投影矩阵分别为和，相对应的 RARE 空域谱为[4～16,22～24]

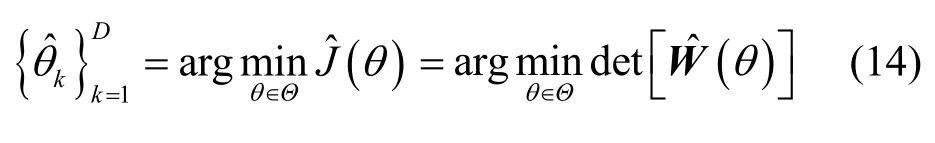
4 有限采样影响下秩减估计器的方位估计性能分析

4.1 正交投影矩阵的扰动分析及其统计特性

定理1[25]设由矩阵特征分解得到信号子空间和噪声子空间的正交投影矩阵分别为和，则有

其中，

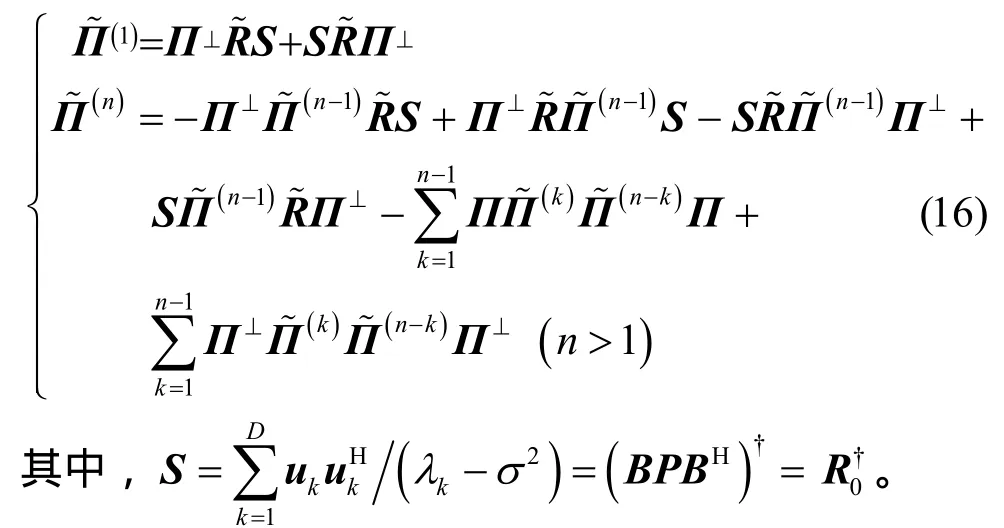
定理 1的证明见文献[25]，它实质上给出了阵列协方差阵扰动量与信号(或噪声)子空间正交投影矩阵扰动量之间的闭式关系，并且不难证明式(16)中的（n）是关于协方差阵扰动量的n次矩阵函数，因此也可以看成是n阶扰动量，又因为，所以有为了对RARE的方位估计性能进行定量分析，本文首先基于定理1给出方位估计偏差与协方差阵扰动量之间的显式关系。然而，方位估计偏差可由不同阶数的误差扰动量累加构成，当推导方位估计均方误差时，通常采用一阶误差分析方法[18,19]得到方位估计偏差的一阶扰动量，它可表示为而相应的均方误差又可表示为但一阶扰动量的均值为零，所以一阶误差分析方法难以获得方位估计偏置的闭式表示。为了得到方位估计偏置的表达式，必须采用二阶误差分析方法[20,21]推导方位估计偏差的二阶扰动量，它可表示为，而相应的偏置又可表示为

为了便于理论分析，这里需要给出关于正交投影矩阵一阶和二阶扰动量的统计特性。首先推导一阶扰动量的二阶统计特性，根据文献[25]可知矩阵中的元素服从联合渐近高斯分布，并且满足

于是有

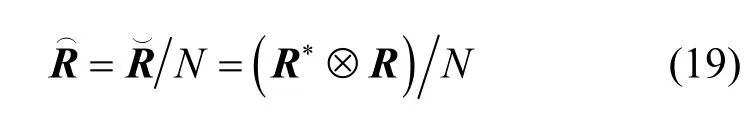
结合式(19)可知其二阶统计量为

式(21)的成立还利用了性质 Π⊥R S =O 。M

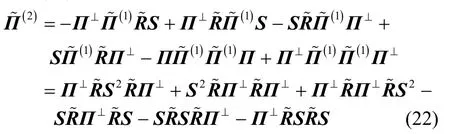
根据式(17)可得等式[25]

基于此可进一步得

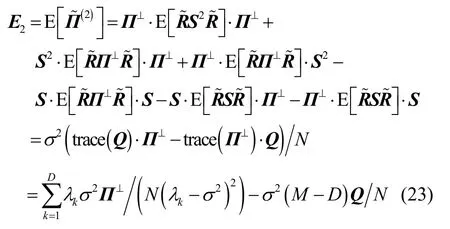
式(21)和式(23)分别对于推导 RARE的方位估计均方误差和偏置起着重要作用。

4.2 秩减估计器的方位估计均方误差

本节将推导RARE的方位估计均方误差。记

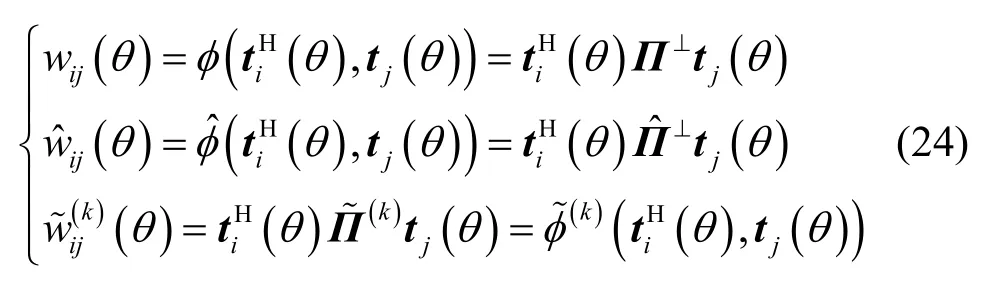
根据矩阵行列式的定义可知 RARE的空域谱为[22～24]

m

根据命题2可推得

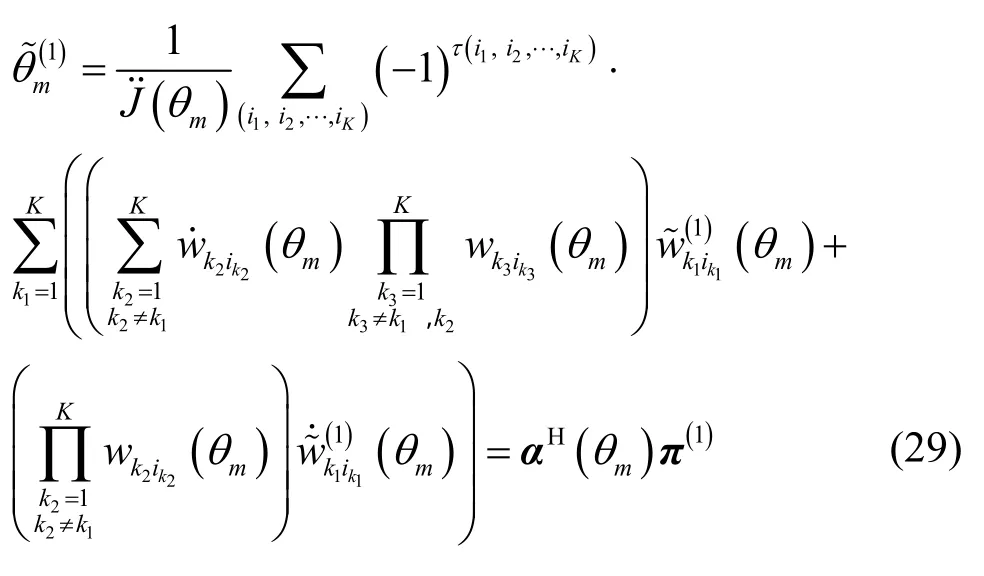
其中， α （ θ）= α1（θ）+ α2（θ） ， α1（θ） 和 α2（θ） 的表达式分别为

此外， ƒ｛·｝ 是满足式(33)的标量函数：

根据式(21)和式(29)可得第m个信源的方位估计均方误差为

2）受冻部位。冻害大多以主干冻伤为主，主要在地面以上30～50 cm，最高可达100 cm，一般树体受冻部位多在树干西北方向，向南方向冻害轻或未受冻。徐香等品种嫁接口及以上部位受冻严重。

为了便于4.4节中推导RARE的整体测向成功概率，这里还需要给出RARE的方位估计方差阵，不妨记方位估计偏差的一阶扰动向量为

则可得RARE的方位估计方差阵为

4.3 秩减估计器的方位估计偏置

本节将推导RARE的方位估计偏置。考虑第m个信源的方位估计，设是对应于真实方位θm的估计值，其二阶扰动量为，则有

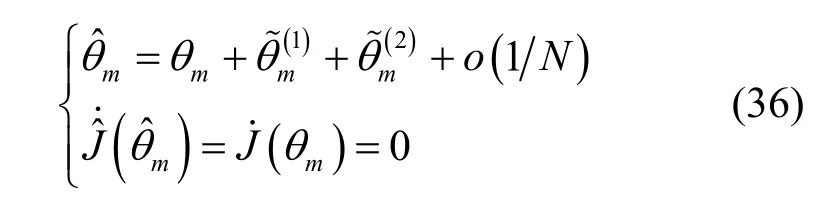
根据命题3和一些代数推导可得

结合式(29)和式(36)可得

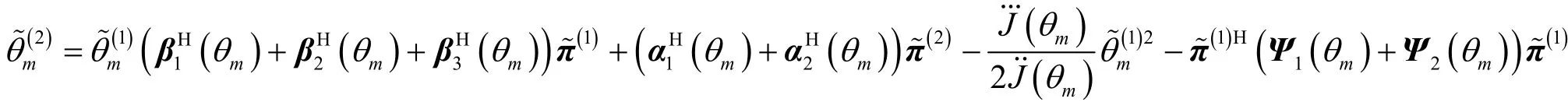
根据式(23)和式(38)可得第m个信源的方位估计偏置为

其中， γ（ θ） = γ1（θ） + γ2（θ） ，而 γ1（θ） 和γ2（θ） 的表达式分别为

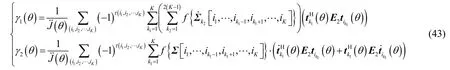
4.4 秩减估计器的测向成功概率

除了方位估计均方误差和偏置外，测向成功概率也是超分辨率谱估计算法的一项重要性能指标，然而相关的理论研究报道并不多见，笔者曾在文献[27]中推导了模型误差影响下 MUSIC算法测向成功概率的计算公式，此外，还在文献[23]中推导了未预期模型误差影响下RARE的测向成功概率的计算公式，而本节则将基于文献[23]和文献[27]中的分析方法推导有限采样影响下 RARE的测向成功概率。所不同的是，文献[23]和文献[27]中并未考虑方位估计偏置，而本文考虑了偏置的影响。

在推导RARE的测向成功概率之前，需要首先确定RARE方位估计偏差的分布特性，根据前面的讨论可知其一阶扰动量服从渐近高斯分布，但其二阶扰动量的概率分布则很难严格推导。文献[28,29]在推导高斯模型误差影响下MUSIC算法的角度分辨概率和方位估计统计特性时，根据李雅普诺夫中心极限定理认为由模型误差二次项构成的分量也近似服从高斯分布，因此MUSIC算法的空域谱及其方位估计偏差也可近似认为服从高斯分布。事实上，在有限采样影响下，方位估计偏差的一阶项仍占据主导地位，而二阶项的讨论可类似于文献[28,29]中的分析方法，于是这里不妨将RARE的方位估计偏差也近似看作为服从渐近高斯分布，并且其方差阵为C (由一阶误差分析方法获得)，而均值向量为μ (由二阶误差分析方法获得)，即其方位估计偏差向量满足需要指出的是，文献[30]在推导有限采样影响下 MUSIC算法的角度分辨概率时也曾做过类似的近似假设，于是能够将角度分辨概率的计算转化为高斯概率密度函数的积分运算，其中的仿真实验也验证了其合理性，而本文第5节的仿真实验也将验证上述高斯假设的有效性。本文在明确RARE方位估计偏差分布特性的基础上，下面将采用文献[23]和文献[27]中给出的关于“测向成功”的定义方式，分别推导针对单个信源和针对整体的测向成功概率。

4.4.1 针对单个信源的测向成功概率

定义 1[23,27]对于第m个信源，若满足条件则认为是“测向成功”。

定义 1中的Δθ表示角度误差容限，根据前面的讨论可近似认为于是第m个信源的测向成功概率为

4.4.2 针对整体的测向成功概率

定义2[23,27]若满足条件“则认为是“第一类整体测向成功”。

显然，为了计算第一类整体测向成功概率需要明确D个信源方位估计偏差的联合概率密度函数，根据前面的分析可知随机向量的概率密度函数可近似表示为

于是第一类整体测向成功概率为

式(46)实质上是立方体上的高维积分问题，它可通过数值积分的方法获得其数值解。

定义3[23,27]若满足条件“则认为是“第二类整体测向成功”。

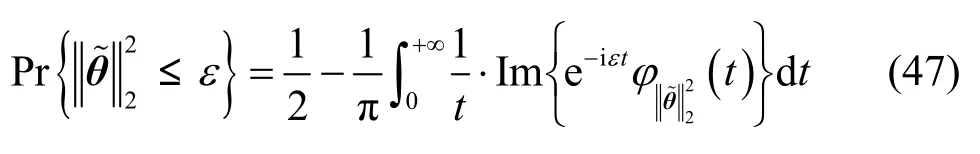
其中， ε = D （Δθ ）2，而是的特征函数，它是计算整体测向成功概率的关键。假设矩阵C的D个非零特征值分别为 ρ1, ρ2,… ,ρD，相应的单位正交特征向量分别为 e1, e2,… ,eD，则根据命题1可得

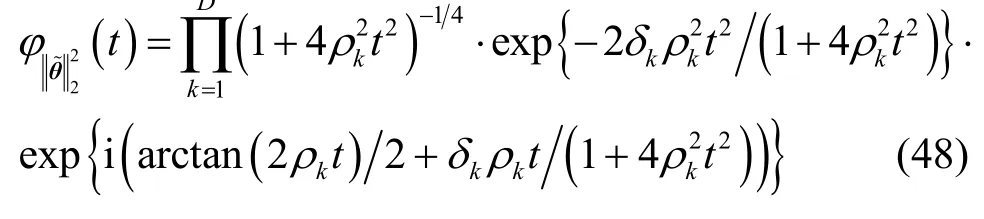
其中，

显然，式(49)中的积分只能通过数值计算的方法获得其数值解，为了计算该数值解，还需要考虑其中的积分函数在 t → 0 和t→+∞时的数值。首先根据洛必达法则容易验证

当t→+∞时，由于积分函数的分子有界，分母将按照递增的方式趋于无穷大，因此该积分函数将以较快的速度趋于零，于是在进行数值计算时，只需要将积分上限设置为一个足够大的正数即可。至此，可给出计算第二类整体测向成功概率的计算方法。

步骤 1 利用式(35)计算矩阵C，根据式(42)计算向量μ。

步骤3 根据特征向量计算标量因子δk=

步骤4 利用数值积分的方法计算式(49)。

至此，本节已经给出了针对单个信源的测向成功概率和两类整体测向成功概率的计算方法，而根据文献[23]和文献[27]中的讨论可知：1)第一类整体测向成功概率一定不大于单个信源的测向成功概率；2)第一类整体测向成功概率必然小于第二类整体测向成功概率，这些结论由它们的定义方式所决定。下面将通过一系列仿真实验验证文中理论推导的有效性。

5 数值实验

这里先做以下几点说明：1)下面是针对文献[4,5]提出的均匀阵列互耦自校正RARE和文献[13]提出的辅助阵元法给出的数值实验；2)尽管 MUSIC算法也是一种特殊的RARE，但在下文的数值实验中都同时给出了RARE和MUSIC算法的性能曲线，并且若不做特殊说明，下文的MUSIC算法是在不存在任何阵列误差的条件下进行的；3)计算测向成功概率的误差容限Δθ均设为0.5º；4)文中所有仿真图中的连续曲线都是理论预测值，即根据文中的理论推导计算所得，而离散点都是仿真实验值(2 000次Monte Carlo独立实验统计结果)。

5.1 针对仅存在单个信源的仿真实验

本节将针对文献[5]提出的均匀圆阵互耦自校正RARE给出数值实验，假设阵列流型为八元均匀圆阵，并且相邻3个阵元之间产生互耦效应，即文中的 3K= ，其互耦因子分别为1、0.12-0.18i和-0.05+0.06i，现仅有单个信源到达该阵列，信源方位为50º。首先，固定半径波长比为1，图1分别给出了RARE和MUSIC算法的方位估计均方根误差、偏置以及测向成功概率随着信噪比的变化曲线；接着，固定信噪比为10dB，图2分别给出了RARE和MUSIC算法的方位估计均方根误差、偏置以及测向成功概率随着半径波长比的变化曲线。

从图1和图2中可以得到如下结论：1)在上述数值实验条件下，3种性能参数的理论值和仿真实验值能够较好地吻合，从而验证了文中理论推导的有效性；2)无论RARE还是MUSIC算法，它们的方位估计精度都随着信噪比和采样点数的增大而提高；3)对于 MUSIC算法而言，其方位估计精度随着半径波长比的增大而提高，但对于RARE而言，其方位估计精度的变化规律则复杂得多，3种性能参数并不是简单地关于半径波长比的单调函数，在上述数值实验条件下，当半径波长比从0.8增至0.9时，RARE的性能会迅速下降，而当半径波长比大于0.9时，RARE的性能又会迅速提高，这一特性由RARE复杂的空域谱函数所决定；4)在上述数值实验条件下，MUSIC算法的方位估计偏置都接近于零，然而RARE却并非如此，从图1(b)中可以看出，当半径波长比固定为 1时，若信噪比低于 12dB，RARE就会存在偏置，而从图2(b)中可以看出，当信噪比固定10dB时，RARE会在半径波长比取值范围为0.8～1之间产生一定偏置；5)在上述数值实验条件下，MUSIC算法的方位估计精度在绝大多数情况下优于RARE，但从图2(a)中可以看出，当信噪比固定10dB且半径波长比大于1.2时，RARE的方位估计均方误差却略小于MUSIC算法。

图1 方位估计均方根误差、方位估计偏置、测向成功概率随信噪比的变化

图2 方位估计均方根误差、方位估计偏置、测向成功概率随半径波长比的变化

这一结论似乎有悖于常理，但仔细分析则并非如此。正如本节开头所指，文中的MUSIC算法是在没有任何阵列误差的条件下进行的，在此处就是指没有互耦效应，因此RARE和MUSIC算法所处理的数据模型是不同的，所以在某些参数条件下RARE的方位估计均方误差反而小于MUSIC算法是有可能出现的。事实上，若RARE与互耦存在的已知的MUSIC算法进行比较，则根据信息论原理可知前者的性能将始终低于后者，因为此时它们两者所处理的数据模型是一样的，这里不妨将RARE和互耦存在且已知的MUSIC算法进行比较，实验条件同图2(b)，并将采样点数固定为300，表1给出了它们的方位估计均方根误差的理论数值，从表中可以看出RARE的方位估计均方根误差始终大于互耦存在的已知的MUSIC算法。

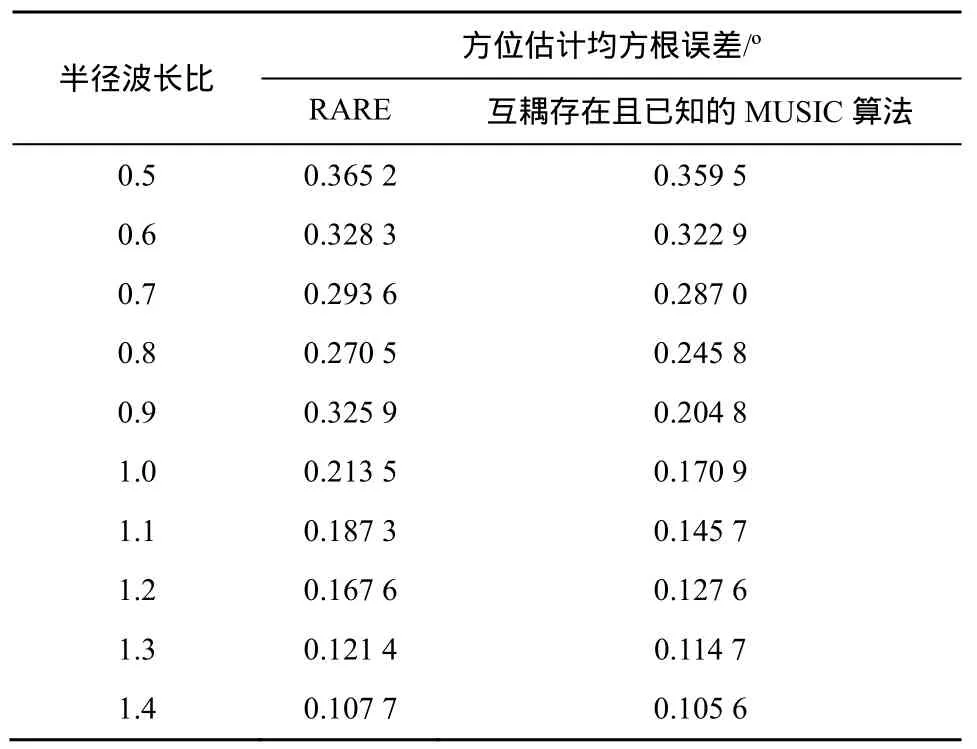
表1 方位估计均方根误差的理论数值

5.2 针对存在2个信源的仿真实验

本节首先针对文献[4]提出的均匀线阵互耦自校正RARE给出数值实验，假设阵列流型为九元均匀线阵，相邻阵元间距与波长比为0.5，并且相邻3个阵元之间产生互耦效应，其互耦因子同上，现有2个等功率相关但不相干信源到达该阵列，它们的相关系数为iπ6

0.1e ，信源方位(指与线阵夹角)分别为 64º和 82º，采样点数为 500。图 3分别给出了RARE和MUSIC算法的方位估计均方根误差、偏置、针对单个信源的测向成功概率和整体测向成功概率随着信噪比的变化曲线。

接着针对文献[13]提出的辅助阵元法给出数值实验，假设阵列流型为六元均匀线阵，相邻阵元间距与波长比为0.5，其中前4个阵元为辅助阵元，即不存在任何幅相误差，并且阵元的幅度因子均设为1，相位因子均设为0º，而后2个阵元存在方位依赖的幅相误差，现有2个等功率相关但不相干信源到达该阵列，它们的相关系数为iπ60.1e ，信源方位(指与线阵夹角)分别为65º和85º，并且后2个阵元对应信源1的幅度因子为1.32和0.78，相位因子为28.7º和-23.8º，对应信源2的幅度因子为0.86和1.25，相位因子为-14.6º和16.5º，采样点数仍设为500。图4分别给出了RARE和MUSIC算法的方位估计均方根误差、偏置、针对单个信源的测向成功概率和整体测向成功概率随着信噪比的变化曲线。

图3 方位估计均方根误差、方位估计偏置、单信源的测向成功率、整体测向成功率随信噪比的变化

图4 方位估计均方根误差、方位估计偏置、单信源的测向成功率、整体测向成功率随信噪比的变化曲线

从图3和图4中可以得到如下结论：1)在上述数值实验条件下，3种性能参数的理论值和仿真实验值仍能较好地吻合，从而进一步验证了文中理论推导的有效性；2)无论是RARE还是MUSIC算法，它们的方位估计精度仍都随着信噪比的增大而提高；3)在上述数值实验条件下，MUSIC算法的方位估计精度始终优于 RARE；4)在上述数值实验条件下，当信噪比较低时，RARE会产生一些偏置，然而MUSIC算法的偏置则仍基本接近于零，只是在图3(b)中，当信噪比小于3dB时，MUSIC算法会有约 0.01º的偏置，事实上，无论是 RARE还是MUSIC算法，当参数条件往坏的方向发展时，它们都会逐渐产生偏置，只是相比而言，RARE更容易出现偏置；5)第一类整体测向成功概率始终不会高于单个信源的测向成功概率，并且第一类整体测向成功概率始终小于第二类整体测向成功概率，这一结论符合文献[23]和文献[27]中的分析结果。

最后，通过仿真实验反映信源相关系数对RARE性能的影响，第1个实验的仿真条件基本同图3，只是固定信噪比为15dB，图5给出了RARE的方位估计均方根误差随着信源相关系数幅度因子和相位因子的变化曲面。第2个实验的仿真条件基本同图 4，固定信噪比仍为 15dB，图 6给出了RARE的方位估计均方根误差随着信源相关系数幅度因子和相位因子的变化曲面。

从图5和图6中不难看出：相关系数的相位因子对RARE性能的影响非常小，但相关系数的幅度因子对RARE的性能会产生一定影响，尤其当幅度因子大于0.8时，RARE的性能会迅速恶化，这是由于相关系数的幅度因子决定了两信源之间的相关性，这一变化规律与MUSIC算法也是一致的(它们都是基于子空间技术提出的算法)。

6 结束语

本文从理论上定量分析了有限采样影响下RARE的方位估计性能，基于文献[25]中给出的信号(或噪声)子空间正交投影矩阵的扰动定理，推导了RARE方位估计偏差的一阶和二阶扰动量，在此基础上分别给出了其方位估计均方误差、偏置以及测向成功概率的理论表达式。针对文献[4,5]中的均匀阵列互耦自校正RARE和文献[13]中的辅助阵元法给出了数值实验，仿真结果验证了理论推导的有效性。本文的结论对于RARE的工程应用具有一定指导意义。

图5 第1个实验下，方位估计均方根误差随着相关系数的变化曲面

图6 第2个实验下，方位估计均方根误差随着相关系数的变化曲面

附录A 对命题1的证明

附录A将对命题1进行简单证明。先对矩阵A进行特征分解可得，于是有

又因为相互独立随机变量和的特征函数等于各自特征函数的乘积，所以随机变量y的特征函数可由式(2)确定。

附录B 对命题2的证明

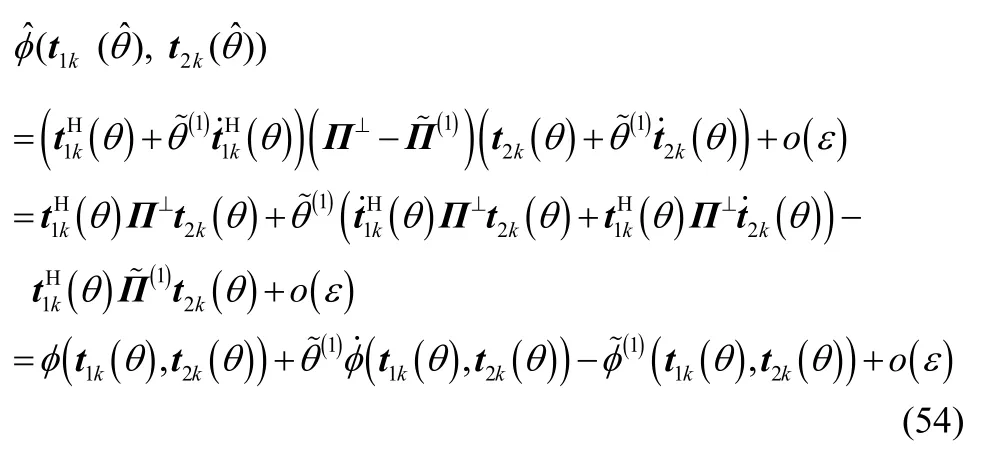
式(4)可通过数学归纳法进行证明，当 K = 2 时显然成立，假设当 K = n -1时结论成立，则当K = n 时可得

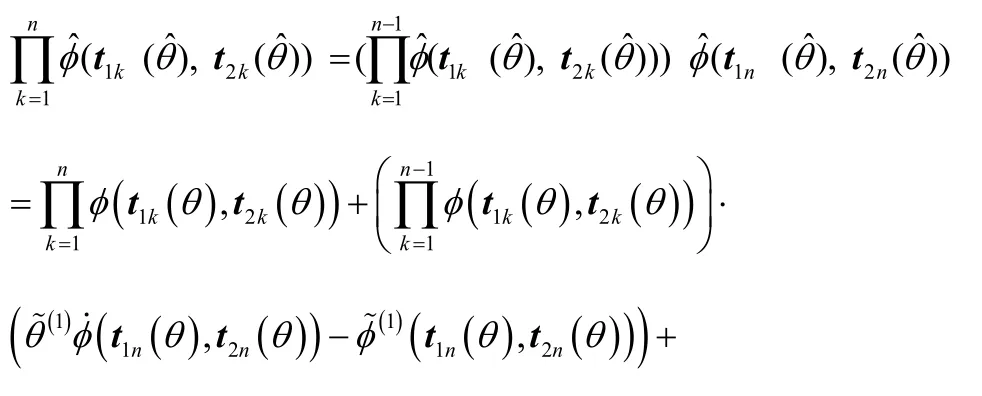
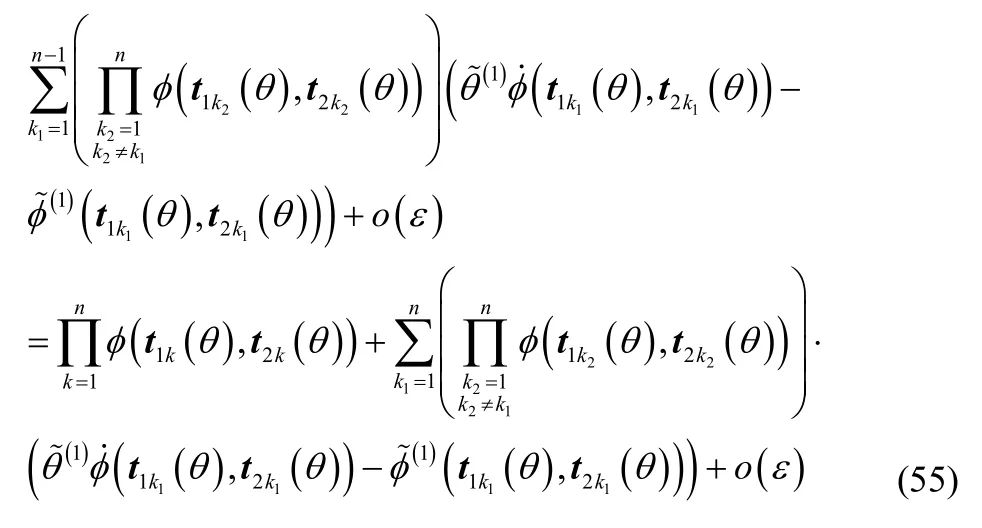
根据式(55)可知当K n= 时式(4)成立，因此命题2成立。

附录C 对命题3的证明

式(6)的证明过程类似于式(4)，可通过数学归纳法进行证明，鉴于篇幅考虑这里不再详细描述。

[1] FRIEDLANDER B, WEISS A J. Direction finding in the presence of mutual coupling[J]. IEEE Transactions on Antennas and Propagation,1991, 39(3)：273-284.

[2] SELLONE F, SERRA A. A novel mutual coupling compensation algorithm for uniform and linear arrays[J]. IEEE Transactions on Signal Processing, 2007, 55(2)：560-573.

[3] WIJNHOLDS S J, VEEN A J. Multisource self-calibration for sensor arrays[J]. IEEE Transactions on Signal Processing, 2009, 57(9)： 3512-3522.

[4] WANG B H, WANG Y L, CHEN H. Robust DOA estimation and array calibration in the presence of mutual coupling for uniform linear array[J]. Science in China Series F： Information Sciences, 2004, 47(3)：348-361.

[5] QI C, WANG Y, ZHANG Y, et al. DOA estimation and self-calibration algorithm for uniform circular array[J]. Electronics Letters, 2005,41(20)：1092-1094.

[6] 吴彪, 陈辉, 杨春华. 基于L型阵列的方位估计及互耦自校正算法研究[J]. 电子学报, 2010, 38(6)：1316-1322.WU B, CHEN H, YANG C H. Study of DOA estimation and self-calibration algorithm for L-shaped array in the presence of mutual coupling[J]. Acta Electronica Sinica, 2010, 38(6):1316-1322.

[7] LIANG J L, ZENG X J, WANG W Y, et al. L-shaped array-based elevation and azimuth direction finding in the presence of mutual coupling[J]. Signal Processing, 2011, 91(5)：1319-1328.

[8] 吴彪, 陈辉, 胡晓琴. 基于Y型阵的互耦矩阵与DOA的同时估计方法[J]. 通信学报, 2010, 31(6)：119-126.WU B, CHEN H, HU X Q. Simultaneous estimation of mutual coupling matrix and DOA for Y-shaped array[J]. Journal on Communications, 2010, 31(6):119-126.

[9] HU X Q, CHEN H, WANG Y L, et al. A self-calibration algorithm for cross array in the presence of mutual coupling[J]. Science China Information Sciences, 2011, 54(4)：836-848.

[10] LIU C, YE Z F, ZHANG Y F. Autocalibration algorithm for mutual coupling of planar array[J]. Signal Processing, 2010, 90(3)：784-794.

[11] CHEN H, BAO Z. Performance analysis of self-calibration algorithm for concentric-UCA[A]. Proceedings of the International Conference on Wireless Communications and Signal Processing[C]. Suzhou, China, IEEE Press, 2010. 1-5.

[12] XIANG L, YE Z, XU X, et al. Direction of arrival estimation for uniform circular array based on fourth-order cumulants in the presence of unknown mutual coupling[J]. IET Microwaves, Antennas and Propagation, 2008, 2(3)：281-287.

[13] WANG B H, WANG Y L, CHEN H, GUO Y. Array calibration of angularly dependent gain and phase uncertainties with carry-on instrumental sensors[J]. Science in China Series F, 2004, 47(6)：777-792.

[14] PESAVENTO M, GERSHMAN A B, WONG K M. Direction finding in partly calibrated sensor arrays composed of multiple subarrays[J].IEEE Transactions on Signal Processing, 2002, 50(9)：2103-2115.

[15] SEE C M S, GERSHMAN A B. Direction-of-arrival estimation in partly calibrated subarray-based sensor arrays[J]. IEEE Transactions on Signal Processing, 2004, 52(2)：329-338.

[16] QI C Y, CHEN Z J, ZHANG Y S. DOA estimation and self-calibration algorithm for multiple subarrays in the presence of mutual coupling[A]. IEEE Proceedings on Radar, Sonar and Navigation[C]. 2006.333-337.

[17] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986,34(3)：267-280.

[18] STOICA P, NEHORAI A. MUSIC, maximum likelihood, and Cramer-Rao bound[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1989, 37(5)：720-741.

[19] STOICA P, NEHORAI A. MUSIC, maximum likelihood, and Cramér-Rao bound：further results and comparisons[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(12)：2140-2150.

[20] XIAO L X, BUCKLEY K M. Bias analysis of the MUSIC location estimator[J]. IEEE Transactions on Signal Processing, 1992,40(10)：2559-2569.

[21] LI F, LU Y. Unified bias analysis of subspace-based DOA estimation algorithms[J]. Control and Dynamic Systems, 1996, 77：149-192.

[22] 王鼎, 吴瑛. 未预期模型误差影响下秩减估计空域谱的统计特性及分辨概率[J]. 应用科学学报, 2011, 29(2)：176-186.WANG D, WU Y. Statistical characteristics and resolution probability of rank reduction spatial spectrum in the presence of unexpected model errors[J]. Journal of Applied Sciences, 2011, 29(2):176-186.

[23] 王鼎, 吴瑛. 未预期模型误差影响下秩减估计器的性能分析[J]. 通信学报, 2011, 32(8)：81-90.WANG D, WU Y. Performance analysis of rank reduction estimator in the presence of unexpected modeling errors[J]. Journal on Communications, 2011, 32(8):81-90.

[24] WANG D, WU Y. Effects of finite samples on the resolution performance of the rank reduction estimator[J]. Science China Information Sciences, 2013,56(1)：1-14.

[25] KRIM H, FORSTER P, PROAKIS J G. Operator approach to performance analysis of root-MUSIC and root-min-norm[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1992, 40(7)：1687-1696.

[26] 张润楚. 多元统计分析[M]. 北京：科学出版社, 2006.32-33.ZHANG R C. Multivariate Statistical Analysis[M]. Beijing:Publishing House of Science, 2006.32-33.

[27] 王鼎, 吴瑛. 模型误差条件下 MUSIC算法的测向成功概率[J]. 应用科学学报, 2010, 28(3)：289-296.WANG D, WU Y. Success probability of direction-finding of MUSIC algorithm with modeling errors[J]. Journal of Applied Sciences, 2010,28(3):289-296.

[28] FERRÉOL A, LARZABAL P, VIBERG M. Statistical analysis of the MUSIC algorithm in the presence of modeling errors, taking into account the resolution probability[J]. IEEE Transactions on Signal Processing, 2010, 58(8)：4156-4166.

[29] FERRÉOL A, LARZABAL P, VIBERG M. On the resolution probability of MUSIC in presence of modeling errors[J]. IEEE Transactions on Signal Processing, 2008, 56(5)：1945-1953.

[30] HARRY B, MICHAEL S W. Statistical characterization of the MUSIC null spectrum[J]. IEEE Transactions on Signal Processing, 1991,39(6)：1333-1347.

[31] DUGINA T N, MARTYNOV G V. Computing the distribution function of the ratio of quadratic forms in normal variables[J]. Journal of Mathematical Sciences, 1991, 53(6)：628-631.