大数据典型相关分析的云模型方法

杨静，李文平，张健沛

（哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001）

1 引言

自2008年9月《Nature》杂志推出名为“大数据”（big data）的封面专栏[1]以来，产业界和学术界便掀起了大数据研究热潮。数据量巨大是大数据的首要特性，通常认为PB级别及其以上的数据称为“大数据”。大数据还具有稀疏价值特性，即大数据所携带的信息在刻画某特定知识方面是冗余的。这些特性为大数据挖掘带来了巨大的挑战。

大数据典型相关分析（CCA, canonical correlation analysis）是大数据研究的重要内容之一，它不仅有助于揭示大数据间的相关关系，而且可提取蕴含于大数据中的低维特征。大数据CCA可用于大数据特征融合[2]、机器学习[3]、数据降维[4]、数据流挖掘[5]等领域。因此大数据CCA具有重要的意义。

大数据CCA研究极具挑战性，其困难不仅源于CCA本身具有的高复杂度，而且也来自大数据巨大规模以及稀疏价值等特性。面向传统数据的CCA方法的高空间复杂度在面临大数据PB级规模时已不再适应。针对此问题，本文拟研究一种基于云模型的大数据CCA方法，期望该方法能克服大数据巨大规模所带来的高复杂度等困难。

云理论是一种实现定量数据和定性概念之间相互转换的不确定性人工智能方法，最早由我国学者李德毅院士提出。云的具体实现称为云模型。云模型在信任评估[6,7]、时间序列挖掘[8]以及图像分割[9]等广泛领域得到了成功应用。然而，将云模型与CCA结合，以用于大数据研究还鲜有学者涉足，本研究拟在此方面展开初探工作。

本文首先根据逆向云发生器生成各云端的数据概要；其次将数据概要发送至中心云端，利用云运算操作产生中心云数字特征；最后根据中心云数字特征，利用正向云发生器产生中心云滴，在中心云滴上施加 CCA操作。中心云数字特征刻画了各云端中数据的语言值，据此产生的中心云滴是原来大数据的不确定性复原小样本。中心云滴在概念粒度上携带了原始数据的重要信息，从这个意义上来说，研究中心云滴不是在原始数据上直接计算，是探讨大数据挖掘的一个良好视角；此外，中心云滴的小样本特性为CCA赢得了效率。

2 基础知识回顾

2.1 CCA

CCA是研究2个随机向量之间相关性的一种常用多元统计方法[10]。给定p维随机向量X和q维随机向量Y，p≤q，CCA的目标是寻找投影向量αk和βk，使得在方差的约束下，Pearson相关系数

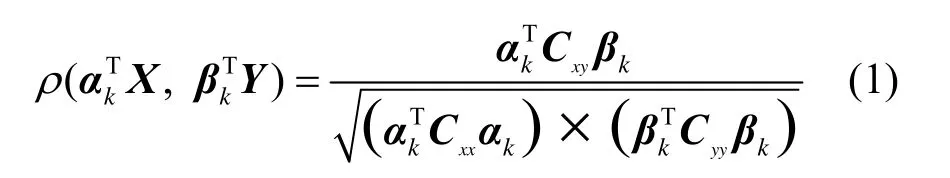
CCA实质是一个最优化问题。以第一对典型变量为例（省略α1和β1下标），即求

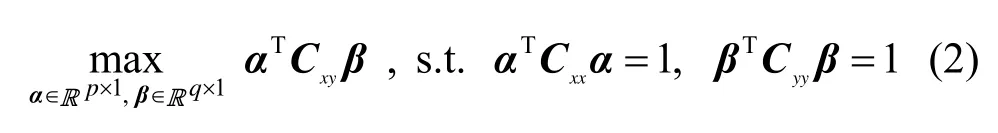
其中，s.t. 表示约束条件，R为实数域。用拉格朗日（Lagrange）乘子法求解式(2)有

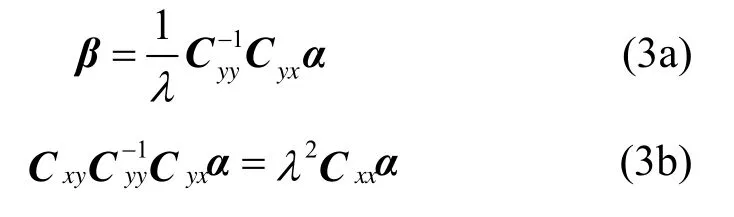
式(3b)是广义特征值问题，由此解出λ和α，代入式(3a)可得β。λ即为所求典型相关系数。CCA有多种解法，如基于 SVD的方法等，具体可参阅文献[11,12]。

2.2 云和云模型

设U为定量论域，C为其上的定性概念，若∀x∈ U 是C的随机实现，且x对C的确定度μ( x )∈ [ 0,1]是有稳定倾向的随机数。

则x在U上的分布称为云（cloud），而x称为云滴（cloud drop）[13]。云理论用期望Ex、熵En和超熵He3个数字特征来表征概念的整体定量特性。在不至混淆时，也将云的 3个数字特征构成的三元组(E x, E n, H e)称为云。

云模型是云的具体实现。由云数字特征产生云滴的实现称为正向云发生器，而由云滴群得到云数字特征的实现称为逆向云发生器。由于正态分布的普适性，建立在其上的正态云是各种云模型中最重要的一种。期望曲线是云理论研究数据集在空间中随机分布统计规律的重要方法，一般方程为

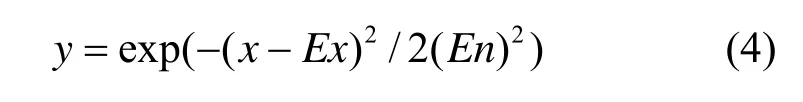
云运算是云理论中用语言值进行计算和推理的重要基础。给定 2个一维云 C1(E x1, E n1, H e1)和C2(E x2, E n2, H e2)，则 C1加 C2之和 C ( E x, E n, H e)可以定义为

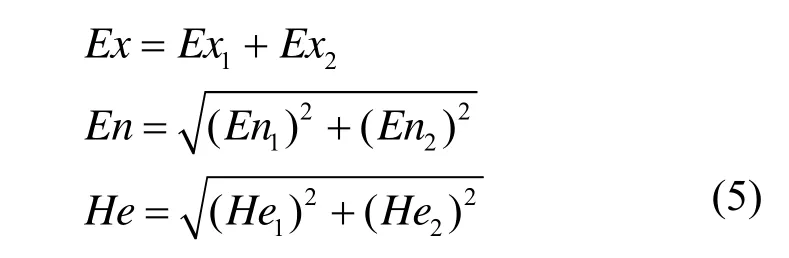
需要补充的是，“云”一词有趣地同时光顾了云计算和云理论，为了不至于混淆，本文所述云端皆指云计算平台中的分布式节点或机群，而其他关于云的词汇，特指云理论中的概念。此外，应将云运算和云计算区别开来。云运算是云理论中对云进行操作的规则，属于不确定性人工智能范畴；而云计算是一种计算范式，强调计算资源的有效利用和整合，与云运算截然不同。

3 相关工作

人类在科研和工程实践项目中收集的大量数据多数具有大数据特性，但将大数据抽象出来作为一门独立科学进行研究还是最近的事[14]。在生物信息学等领域，Benjamin等人深入研究了在系统神经生物学领域担当重要角色的生理电大数据压缩及存储等问题[15]；Aronova等人将生物学研究中收集的数据视为大数据，从大科学（big science）视角挖掘这类数据蕴含的重要知识[16]；Werner则更进一步，从方法论角度分析了如何应对大数据生物学带来的挑战[17]。

在数据挖掘等领域，Alfredo等人从数据仓库和OLAP等视角分析了多维大数据研究存在的问题以及研究趋势[18]；Steven等人研究了大数据挖掘中的在线特征选择问题[19]；Simon等人基于模糊查找词典（fuzzy find dictionary）研究了一种面向数据流大数据的数据流聚类方法[20]；John研究了大数据上的并行学习问题[21]。

在面向大数据的程序开发和存储等方面，Thomas等人探讨了如何在大数据上构建程序实现问题[22]；Yu等人提出了一种可扩展的用于大数据分析的分布式系统[23]；Kyuseok以及Jens等人同时探讨了 MapReduce架构在大数据分析中的应用[24,25]；Divyakant等人分析了大数据及云计算现状和研究挑战[26]；Huiqi等人研究了在云平台上进行可视聚类的一种方法体系[27]。此外，也有学者开始涉足大数据安全方面的研究，如Colin等人探讨了大数据中存在的安全问题及解决策略[28]。

大数据研究还刚刚起步，尽管有学者探讨了基于云计算平台的大数据存储方法，但未发现关于大数据 CCA的研究报告，也未发现在此方面基于云理论的研究方法，期望本研究能对此做出些许初探性工作。

4 大数据CCA方法

本节重点研究基于云模型的大数据 CCA方法（BDCCA, big data CCA）。首先阐述面向大数据的云架构，其次重点探讨端点云的生成方法，再次研究端点云的合并技术。下文约定运算符,＜··＞为欧氏内积，而⊗为Hadamard积。

4.1 面向大数据的分布式云架构

就容量而言，PB级数据量被认为是大数据的显著特性，这一特性使得大数据一般通过机群等分布式方式存储。迄今为止，云平台是大数据存储的理想载体。本研究假设大数据以分布式方式存储在云端。图1刻画了所提出的由若干个云端构成的大数据分布式云架构。

此云架构从功能上分4层：1）顶层为数据存储层，其中，第i个云端存储第i段数据Datai；2）第2层为多维逆向云发生器（MBCG, multidimensional backward cloud generator）层，其核心任务在于由原始数据产生各云端的云，即端点云；3）第 3层为中心云端（center node），该层主要进行云合并运算，并用于产生和存储中心云滴；4）第 4层为应用层（applications），基于中心云滴，在此层可进行CCA等挖掘或分析任务。

在大数据分布式云架构中：1) 根据多维逆向云发生器MBCG，由第i个云端中的数据Datai产生端点云 Ci(E xi, E ni, H ei)，简记为 Ci；2) 将 Ci传送至中心云端的云收集器（collector）；3) 将云收集器中的云传送至多维云合并节点（MCC, multidimensional cloud combiner）；4) 根据多维云合并运算，将所有云 Ci合并为中心云 C ( E x, E n, H e)，简记为C；5) 将中心云C传送至多维正向云发生器(MFCG, multi- dimensional forward cloud generator)节点；6)根据MFCG，由中心云C产生中心云滴；7)应用层中CCA等任务到中心云端获取中心云滴，并据此进行相应的挖掘任务。

此云计算架构用于处理大数据是合适的。1)各云端向中心云端仅传送数据概要，即由云数字特征构成的三元组，如此小的数据量传送是快速的；2)由中心云产生的中心云滴群规模往往较小，这有助于提高CCA的运算速度。

4.2 BDCCA执行流程

BDCCA的基本思路在于：1)在各云端利用逆向云发生器根据当前云端中数据并行生成云（即云数字特征）；2)将各端点云发送至中心云端，利用多维云合并操作，在中心云端产生中心云；3)根据中心云，利用正向云发生器产生中心云滴；4)在中心云滴上施加CCA操作。图2描述了其执行流程。

图1 大数据分布式云架构

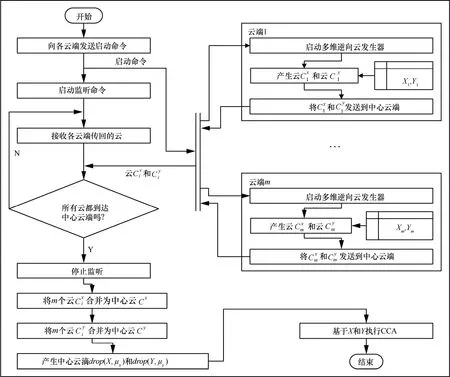
图2 BDCCA执行流程

数据在每个云端分为 Xi和 Yi两部分，其中，X ∈Rp×ni和 Y ∈Rq×ni，n为第i个云端中的样本数

i ii目，p为 Xi的维数，q为 Yi的维数。特别地，同类数据的维数在所有云端都一致，而样本数目可以不同。此外，云端个数m、各云端标识符 Ni、云重要度向量 η = ( η1, η2,… ,ηm)T以及中心云滴数目ω等需预先设定。流程执行结束后，输出典型相关系数向量ρ以及对应典型相关向量为列的矩阵U、V。基于式(3)，可通过特征分解或SVD等方法求解X和Y的典型相关系数和典型相关变量，具体可参阅文献[11]。本文将采用文献[30]的多维正向正态云发生器产生中心云滴群 d rop(X,μx)和 d rop(Y,μy)。限于篇幅，此两点不再赘述。

图2所示流程中，产生各端点云以及在中心云端进行云合并是关键，后文将分别详述这两点，一方面后文将对多维逆向云发生器进行改进，使之适宜于在大数据环境下产生各端点云；另一方面将提出一种一次合并多个多维云的方法，以提高大数据环境下云合并运算的效率。

4.3 端点云生成

所谓端点云的生成，是指根据逆向云发生器，由云端中数据产生云的过程。本文采用无确定度的多维逆向正态云发生器[30]作为端点云的生成模型。

尽管已将大数据存储于分布式云架构各云端（如图1所示），但是由于大数据的巨大容量特性，在每个云端所存储的数据量往往还较大，现存多维逆向正态云发生器不再满足大数据环境下计算效率的要求，对之加以改进是必要的。

为了提高多维逆向正态云发生器在大数据环境下产生云的效率，本文基于随机采样法，采用启发式云生成策略，将多维逆向正态云发生器拓展到大数据情形。

4.3.1 大数据随机采样

本文借鉴随机子空间法[29]思想，在各云端进行大数据随机采样。设各云端将大数据分为若干块，首先对每块按照相同划分方式将其分割成s个子块；然后将所有块中相同位置的子块转换成列向量并进行组合，形成一个子块集，如图3所示。

基于划分的数据块，在每个子块集上执行随机采样。对第i个子块集 Ti，根据随机子空间法思想，随机产生 r*维索引向量 Ii={j1,j2, … , jr*}，r*＜r，r为子块集大小。将所有子块集中产生的索引向量按下标升序组合为 I = {I1, I2,… ,Is}。对每个云端数据X和Y分别执行上述操作。最后在与索引向量对应数据上执行CCA操作。

4.3.2 云生成的启发式策略

在每个云端，云的产生采用启发式策略。其基本思想是，在每个云端迭代地进行若干次不重复随机采样，将每次迭代时抽取的样本加入之前的样本中，每次迭代后进行云更新，若第i次迭代后所生成的云Ci与迭代前的云Ci-1之差ΔCi小于给定阈值或迭代次数超过预设阈值，则迭代终止。迭代过程中，若当前迭代的云差异 ΔCi正向偏离前一次迭代的云差异 ΔCi-1，即 ΔCi- ΔCi-1＞ δ ，则下一次迭代时将加大随机采样的样本容量；反之若 ΔCi负向偏离 ΔC，即 ΔC- ΔC≤ δ ，则下一次迭代

i-1i i -1时将减小随机采样的样本容量。其中，δ≥0，δ为常量。

此策略的2个关键问题在于，其一每次迭代后云的更新；其二相邻两次更新所生成云之间差异的刻画或度量。

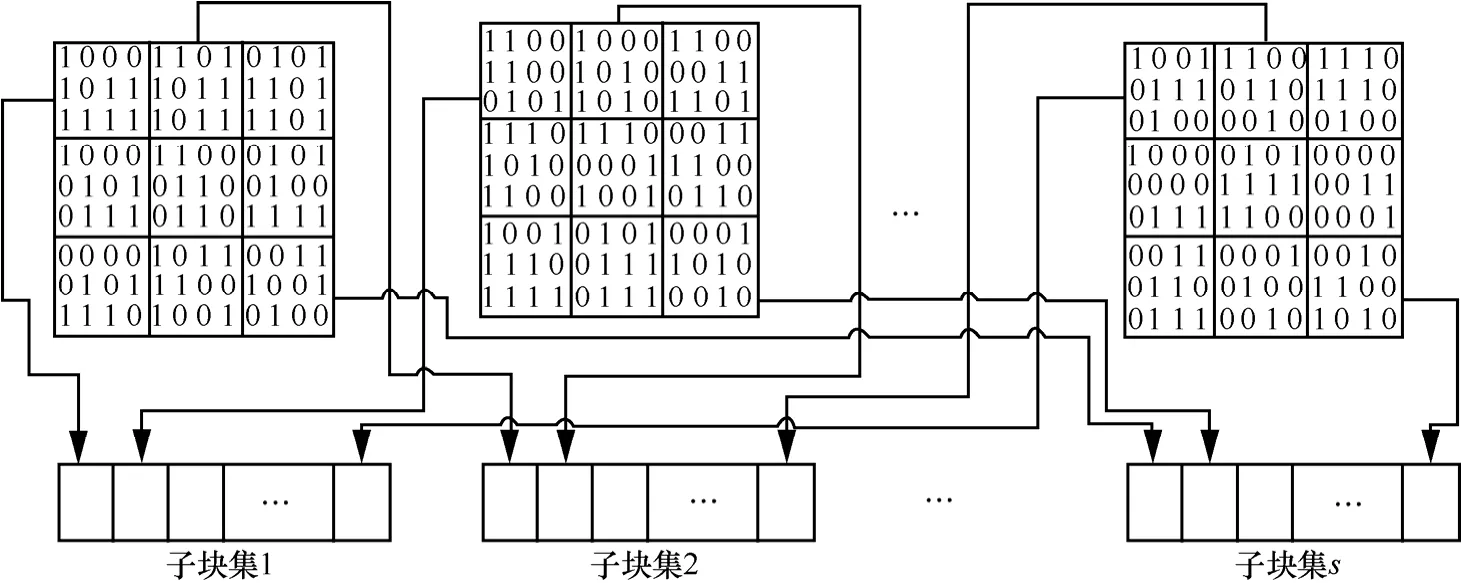
图3 数据子块划分

4.3.3 云的部分增量式更新

每次迭代后的云更新是云的启发式生成策略需要解决的首要问题。云更新即是云期望熵和超熵的更新。其中

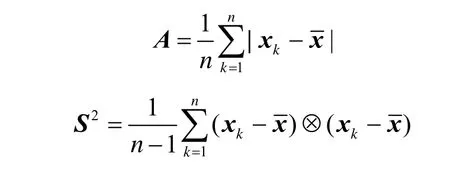
若记

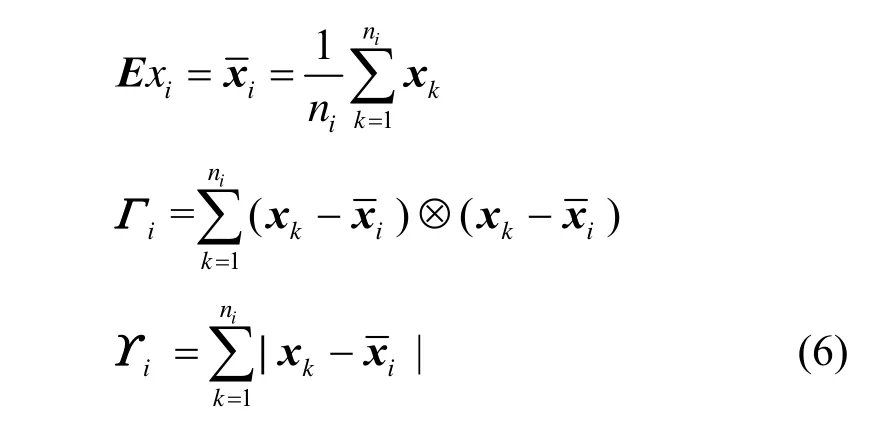
其中，ni为第i次迭代后的样本总容量，而˜为第i次迭代进行随机采样所得的样本容量，显然云增量式更新的本质在于：①用Exi-1刻画Exi；②根据Γi-1求解Γi；③由Υi-1计算Υi。本研究主要更新前两者，故称为部分增量式更新。

这只需注意到

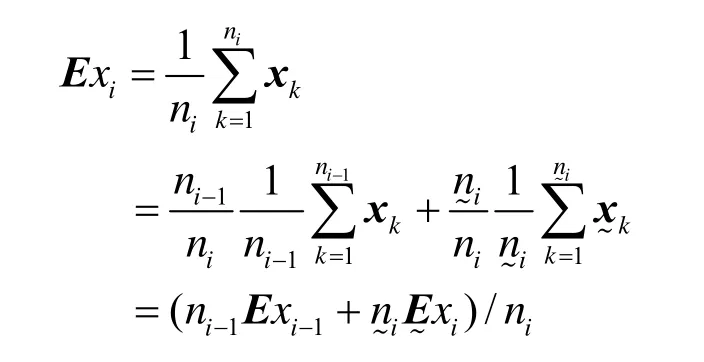
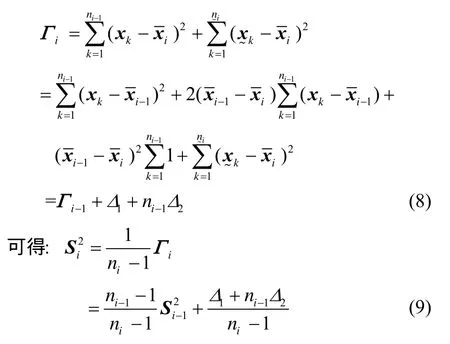
由于绝对值缺乏良好的代数性质，因此要获得A的增量表达式是困难的。本研究在迭代过程中只需跟踪云期望向量Exi和中间向量Γi即可，而不需跟踪Υi的改变量。定理1阐述了其理由。

所以可得 ΔΥi→0。

定理1表明，若迭代终止条件为相邻两次更新生成云的差异足够小，则只需考察云期望向量 E xi和中间向量Γi的改变量是否小于给定阈值即可。

需要补充的是，云部分增量式更新的根本目的不是为了增量式求解各端点云，而是云生成的启发式策略中进行不重复随机采样时用于判断迭代的终止条件，因为部分增量式更新具有较快的速度。

4.3.4 云差异的弦度量

相邻两次更新所生成云之间差异的刻画是云启发式生成策略需解决的又一重要问题。由定理 1可知，用云期望向量Exi及中间向量Γi的改变量来刻画第i次迭代后所生成云 Ci与迭代前的云 Ci-1之差异 ΔCi是合适的。即

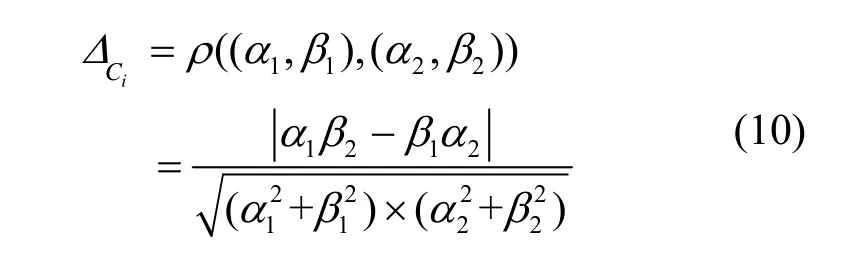
这种间接度量方式除了具有相邻云之间差异的刻画能力外，其另外2个优点在于：①规范性，即 ΔCi∈[0,1]；②异常值的不敏感性，显然Exi和Γi对异常值是敏感的，当异常值出现时，可对弦度量对应的Riemann球面做一个适当旋转，此旋转对应着异常值的 l2范数的一个变换，变换后的值为非异常值，其优势是保持弦度量不变。限于篇幅，本研究不再深入探讨异常值的检测及处理等细节。

4.3.5 改进的多维逆向云发生器算法

基于大数据随机采样法以及启发式的云生成策略，本文对无确定度的多维逆向正态云发生器[30]进行改进，使其适宜于大数据环境下云的快速生成。改进后的算法如下。

算法1 大数据多维逆向云发生器BDMBCG。

输入：子块数目s，初始抽样率 r0，云差异阈值ε。

输出：云 C ( E x, E n , H e )。

1) 初始化：将分块存储在当前云端的数据按4.3.1节所述的数据子块划分方式将其分割成s个子块，并求每个子块大小 s0，置 n = r0s0，置r为小于n的随机正整数。

2) 进行两次容量分别为n和r的不重复随机采样，并根据式(6)计算均值向量 E x0和 E x1以及中间向量Γ0和Γ1，再根据式(10)求云差异ΔC。

3) WHILE ΔC＞ε且数据未抽样完时。

4) Ex0=Ex1，Γ0=Γ1，n=n+ r。

5) 执行容量为r的不重复随机采样，当所剩样本不足r时，抽取剩余样本的。

6) 根据式(7)更新Ex1，并根据式(8)更新Γ1。

7) 根据式(10)求云差异 ΔC'。

8) IF ΔC'-ΔC＞ ε/2

9) 产生小于r的随机正整数t，并置r=t；

10) ELSE

11) 产生介于(r, s0)之间的随机正整数t，并置 r=t；

12) ENE

13) 置 ΔC=ΔC'。

14) END //End While

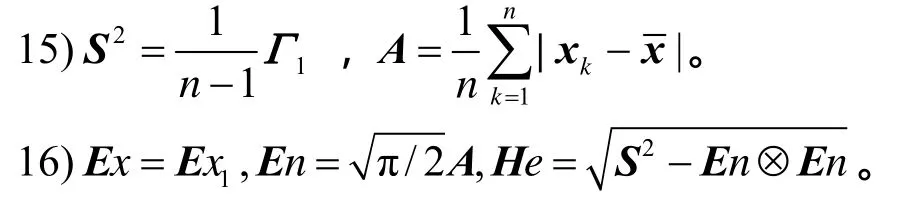
算法1的最后两步表明，尽管云部分增量式更新的根本目的不是为了增量式求解各端点云，但却达到了部分增量式求解的目的，因为求解云 C ( E x,E n , H e )时，只重新计算中间量A，其余量直接应用算法在启发式迭代过程中增量更新的值。

注：1)算法1在各个云端执行，本研究假设数据X和Y作为云端公共变量可直接访问，因此算法输入省略此数据项；2)每个云端数据X和Y的容量往往不相等，由于 CCA要求输入的两组样本容量一致，因此算法执行后还需进行一次随机采样，其操作在小样本容量对应的数据上进行，所抽取样本量为算法1执行后获得的两组样本量之差值。

4.4 多维云合并

在式(5)对应的云合并运算中，每次仅能进行一对云加法运算，如果通过反复调用方式每次合并一对云，每合并一次，云的总个数仅减少一个，因为新生成的云还需要加入合并操作，这在云端较多时将增大时间开销，特别在大数据环境下，其效率会遭受质疑；另一方面，式(5)也未顾及2个云重要性的差异，在大数据环境中，由于受数据收集或存储策略等差异的影响，不同云端的数据可能存在重要性差异，因此各云端传送到中心云端的云的合并应体现各云端之差异。

针对前述不足，本文借鉴文献[30]用于概念粒度提升的跃升策略的相邻云合并思想，提出了一种适宜于大数据的云合并运算方法。

给定 m个p维云 Ci(E xi, E ni, H ei)(i = 1 ,2,…,m)，以及刻画每个云重要度的向量 η = ( η1,η2,… ,ηm)T，∑ηi=1，记

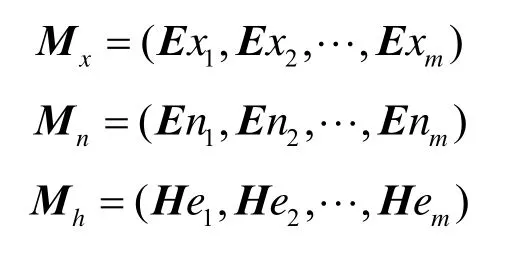
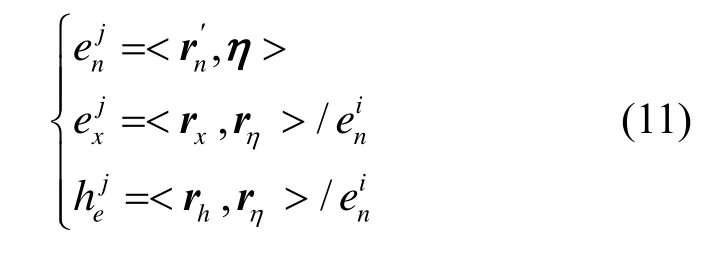
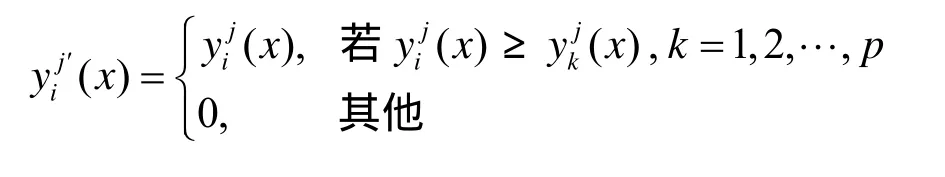
则有

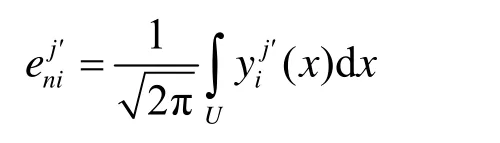
其中，U为第i个p维云 Ci的第 j个维度对应论域， i = 1,2,… ,m; j = 1,2,… ,p 。

与已有方法相比，本文提出的云合并方法呈现出3个特点：1)能对各云端传入中心云端的云进行一次性合并；2)云合并中体现了不同云端的重要性差异；3)合并的是多维云，而非一维云。

5 仿真实验及结果分析

5.1 实验数据及仿真云平台

实验涉及3个数据集。

1) 带噪声的线性数据集LN：这是一个合成数据集，数据X和Y每个属性来自于线性数据，然后叠加符合高斯分布N(1,2)的样本扰动每个属性值。每次产生的数据包括10个维度。

2) 真实数据集PAMAP2：这是对18个不同物理活动进行监视所收集的数据（http：//archive.ics.uci.edu/ml/datasets/PAMAP2+Physical+Activity+Mon-i toring），包括3 850 505行记录，含52个属性。实验选取的属性为惯性测量单元 IMU（inertial measurement units），前两组实验选取手部 IMU（IMU hand）的前10个属性，而第三组实验将手部IMU作为一组（包括 17个属性），而胸部 IMU（IMU chest）作为另一组（包括17个属性）。

3) 真实数据集IDS：网络入侵检测数据集IDS[31]记录了网络链接中正常链接和攻击性链接（intrusions or attacks）的行为数据，共包括494 021条记录，含41个属性。实验选取其中的连续属性（包括34个）进行测试，前两组实验选取前10个属性；第三组实验将前12个属性为一组，其余为另一组。

实验前已删除数据集中具有缺失值的记录，且对每个属性在均值4倍方差外的值用均值替换。

CCA以及多维云发生器对数据约束较少，一般认为，只要总体接近正态分布的实数都可采用。选择PAMAP2和IDS数据集的理由在于它们是得到大量文献广泛采用的标准数据集，而且其容量较大，已接近仿真实验平台的资源上限。

实验从上述3个数据集中选取的每个属性都是总体接近正态分布的实数。图4是从PAMAP2数据集手部IMU中随机挑选出的两列数据（IMU6和IMU12）的分布直方图。数据已规范化为均值0，方差1。设置了25个云端，将数据均分为25个相邻块，每个云端分配一块。其中，图 4(a)为总体分布直方图，而图 4(b)﹑图 4(c)和图 4(d)分别为第3号﹑17号和23号云端中的数据分布直方图。

由图4可以看出，不论是总体数据还是分配到各云端的数据都接近正态分布；此外，不同云端的均值偏移不同，且方差范围有所区别，此现象说明4.4节研究多维云合并是必要的。笔者在做本实验前还对手部IMU其他属性、胸部IMU的各属性以及LN和IDS数据集的连续属性都进行了类似的分布情况观察分析，结果与在IMU6和IMU12上的观察结果相似，篇幅所限，不再赘述。

因此，尽管所选数据集与真实大数据在容量上有一定的差异，但就仿真而言，数据容量﹑数据总体分布和各云端的数据分布等都有一定的代表性。

实验在单台微机上通过仿真完成。为仿真数据在各云端的存储，实验为每个云端创建一个文件夹，每个文件夹下存储若干纯文本文件，每个文本文件存储一个数据块。每个实验开始前，先将各数据集切分为相邻块并存储到对应文本文件中。

实验为每个云端启动一个独立线程，所有云端对应线程并行执行。每个线程从所属云端对应文件夹下读取相应数据，并分配一块内存用于存储相应数据。各线程根据读取的数据生成各端点云。若内存资源不足时，正在读取数据的线程挂起，当内存资源可用时再唤醒。在需计算运行时间的实验中，线程从挂起到唤醒所耗时间忽略。

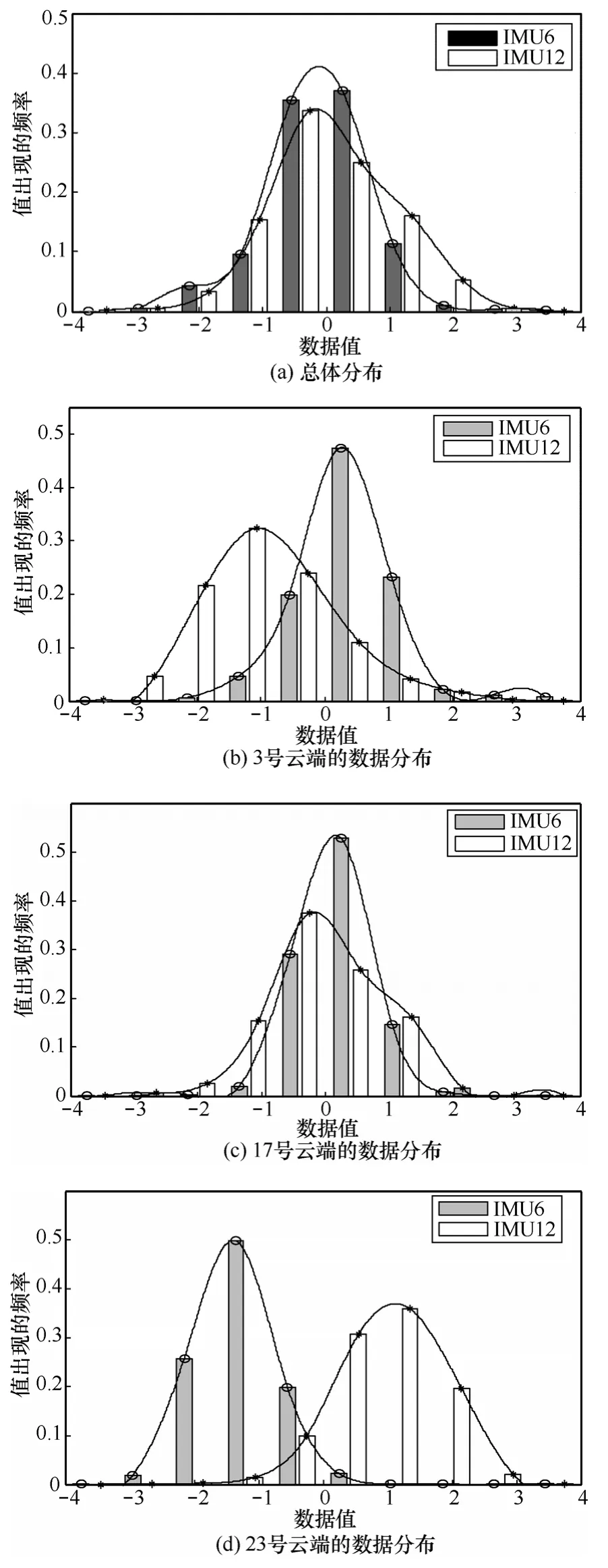
图4 IMU6和IMU12分布直方图

为中心云端启动一个独立线程，并分配一块互斥访问的内存，用于存储各云端传回的云。当所有端点云都传回后，中心云端对应线程基于此内存块中的云完成云合并、中心云滴产生以及CCA运算。

实验通过 C#语言实现，在 Microsoft Visual Studio 2010 Ultimate-CHS环境中完成，作图工具选用 MATLAB R2011a。实验计算机配置为双核 2.8 GHz CPU、4.0 GB内存，操作系统为 Windows 7 Professional。

5.2 实验一：各参数对端点云生成的影响

为验证本文改进的多维逆向云发生器BDMBCG的有效性，本实验评估各参数对端点云生成的影响。为叙述方便，将改进前的多维逆向云发生器记为MBCG。由于BDMBCG在每个云端运行，因此本组实验设置云端数目为1，即在1个云端观察，并设数据集在每个云端分为10块存储。

需考察的参数包括数据子块数目s、初始抽样率 r0和云差异阈值ε。实验将云 C ( E x, E n, H e )视为Rp×3上的子空间，p为维数，用算法改进前计算出的云 C1和改进后所得的云 C2对应的列子空间S1=col(C1)和S2=col(C2)的距离 d ( S1, S2)作为误差error的度量，定义为

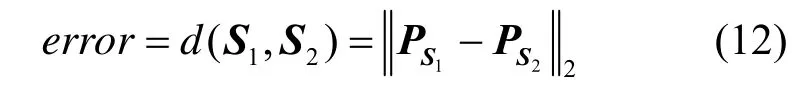
ii上的正交投影算子， i = 1 ,2。

需要补充的是，式(12)与式(10)刻画的2种云差异的区别：①条件不同，式(12)需求出云期望、熵和超熵后才有意义，而式(10)只需给出云期望向量和中间向量Γ；②目的不同，式(12)用于直接度量2种算法产生的云之间的差异，而式(10)用于间接度量同一算法在云部分增量式更新过程中相邻时刻产生的云之间的差异。由于算法1执行后云已经生成，因此用式(12)刻画BDMBCG生成的云与MBCG生成的云之间的差异是合理的。由上述两点区别得出的结论是，引入式(10)和式(12)是必要的，而且不可用一方代替另一方或交换其位置。

每组实验重复100次，以观察不同参数下云的平均差异和计算时间。每次生成LN数据200 000条记录，每条记录包括10维；从PAMAP2数据集随机抽取200 000条相邻记录，其属性选取为手部IMU前10个属性；并从IDS数据集中随机抽取200 000条相邻记录，其属性选取前10个连续属性维度。

首先，考察数据子块数目s对生成云的影响及计算时间的差异。初始抽样率00.35r= ，云差异阈值0.1ε=。图5为误差比较图，而图6为3个数据集上的平均计算时间比较图。

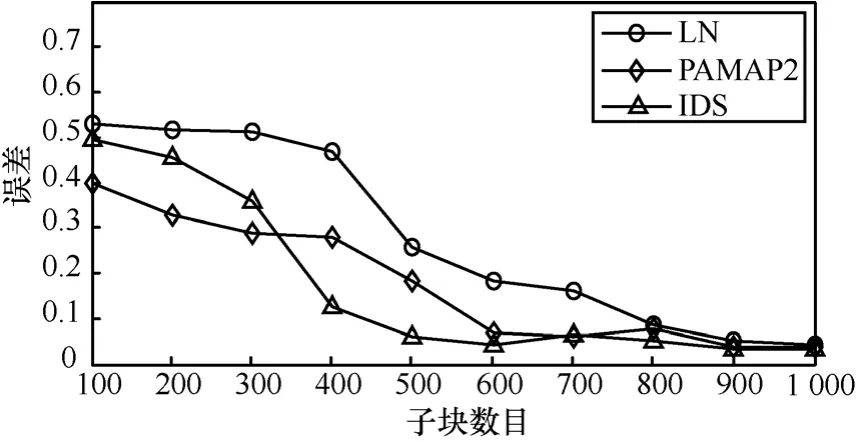
图5 不同子块数目下所生成云的误差

由图 5可见，随着子块数目s的增大，误差逐渐减小。当s增加到1 000时，误差已接近0.05。此现象表明，适当增大子块数目有助于提高计算精度。但图 6却表明，随着子块数目的增大，BDMBCG所需时间略有上升。因此在一定精度范围内，子块数目选择适中为宜。此外，真实数据集PAMAP2和IDS上的误差比合成数据集LN上的误差略小。

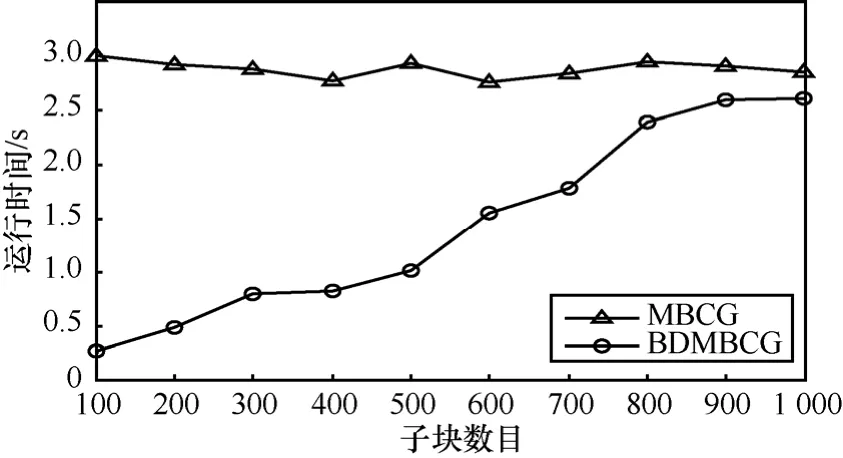
图6 不同子块数目下平均运行时间

其次，评估初始抽样率0r对生成云的影响。数据子块数目400s=，云差异阈值0.1ε=。图7为误差比较图，而图8为不同初始抽样率0r的平均运行时间。

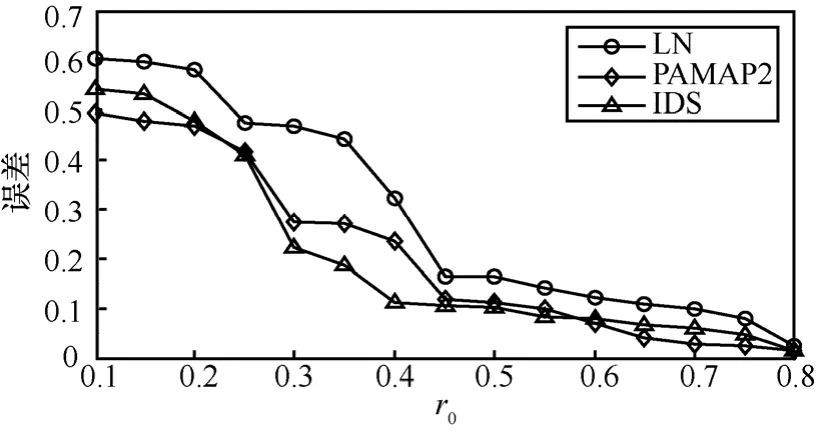
图7 不同初始抽样率下所生成云的误差

由图 7可以看出，在00.3r≤ 时各数据集上误差都较大；当0r在 0.20～0.45范围内时，误差下降趋势明显；而此后误差逐渐接近0.05左右，且波动较小，其趋势几乎延续到00.8r= 。但是，并不是初始抽样率越大越好，观察图8可以发现，当0r变小或增大时，3个数据集上平均运行时间持续增加。

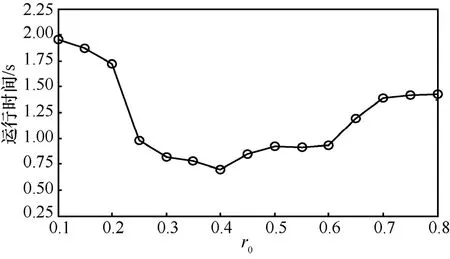
图8 不同初始抽样率下平均运行时间

再次，观察云差异阈值ε对生成云的影响及计算时间的差异。初始抽样率 r0= 0 .4，数据子块数目 s = 4 00对。图9为误差比较图，而图10呈现了3个数据集上的平均运行时间。由图9可以看出，当 ε ≥ 0 .15时，误差持续增大。图10表明，生成云的平均运行时间随着云差异阈值的增大不断减少。结合两图观察发现，当ε介于[0.08,0.15]时，能获得一个兼顾较低误差和较少运行时间的折中方案。

图9 不同云差异阈值下所生成云的误差

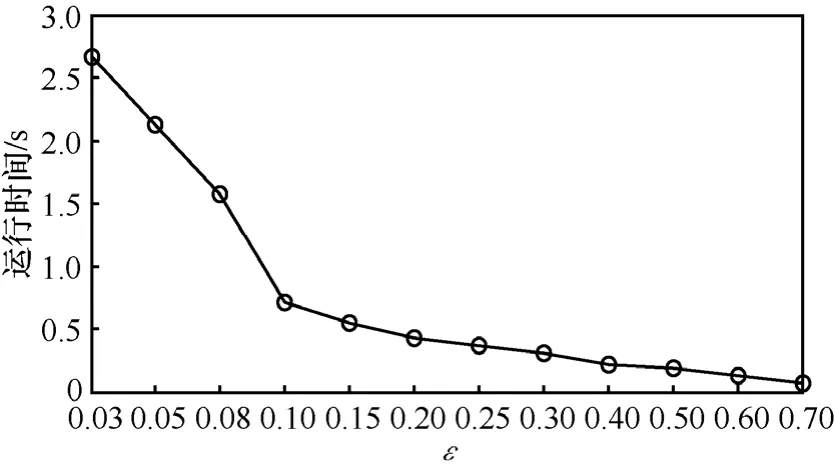
图10 不同云差异阈值下平均运行时间

5.3 实验二：多维云合并运算的效率分析

本实验将式(5)对应的原始云合并方法（记为“original”）与本文提出的一次性合并多个多维云的云运算方法（如式(11)所示，不妨记为“new”）进行比较，评估不同云端数目对云合并效率的影响。对于式(5)对应的原始云合并，通过反复迭代，每次合并2个云，将前一次合并后的云加入当前云的集合再次合并，直至最终合并为一个云为止。

对于同一云端数目 nci，实验重复进行50次。第i次实验中，云重要度皆为1/nci。每次实验生成维数为 10的 LN数据 2 nci× 1 05条记录；并从PAMAP2数据集和IDS数据集中各随机抽取 2 × 105条相邻记录 nci次，属性选取与实验一相同。按抽取顺序将数据平均分配到 nci个云端。之后在每个云端并行调用算法1的BDMBCG( s = 4 00、r0= 0 .3、ε= 0 .1)生成每个端点云，并将生成的云传回中心云端。本实验仅仅评估在中心云端上合成中心云的效率。

图11为不同云端数目下，在3个数据集上云合并的平均运行时间比较图。由图 11可以看出，随着云端数目的增大，原始的云合并操作所需时间迅速上升，而本文提出的一次性合并多个多维云的操作所需时间上升幅度却相对较小。此现象表明，本文提出的云合并操作对于所提出的大数据分布式云架构是合适的，云端数目增大并未显著提高云合并的时间开销。

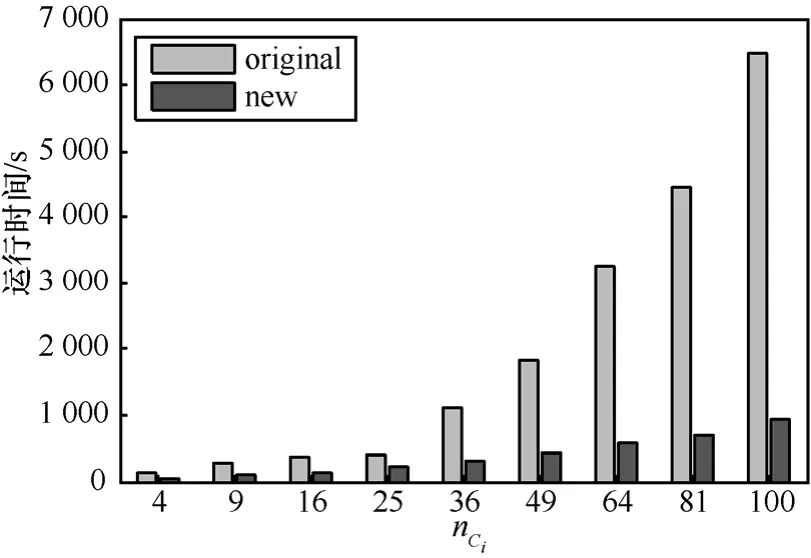
图11 云合并运行时间比较

5.4 实验三：BDCCA的有效性评估

为验证本文所提BDCCA的有效性，本组实验将 BDCCA 与经典 CCA（记为 NaiveCCA）、ApproxCCA[32]和LS-CCA[33]进行对比分析，考察不同云滴群大小、不同云端数目以及不同数据总容量下，典型相关系数的精度以及BDCCA的执行效率。

典型相关系数的精度用其误差error刻画。error定义为 NaiveCCA在原始大数据上所得典型相关系数 rNavieCCA分别与其他几种方法所得典型相关系数之差的绝对值，即

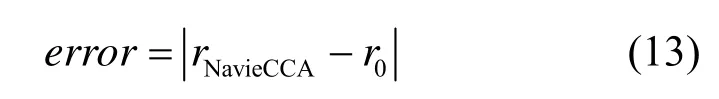
其中， r0取 rBDCCA、rApproxCCA或rLS-CCA。rBDCCA表示BDCCA在云滴群上所得的典型相关系数，而rApproxCCA和rLS-CCA分别表示ApproxCCA和LS-CCA在原数据上所得的典型相关系数。

基于BDCCA求典型相关系数的过程为：对于每个实验，首先在每个云端并行调用算法 1的BDMBCG生成每个端点云，并将生成的云传回中心云端；其次根据式(11)进行云合并；第三采用文献[30]中的多维正向正态云发生器产生中心云滴群drop( X,μx)和 d rop( Y,μy)；最后在X和Y上执行CCA操作。

本节所有实验在每个云端前两步的参数设置同实验二，且所有实验在数据集 PAMAP2和 IDS上进行。在PAMAP2数据集上，实验将手部IMU作为一组（包括17个属性），而胸部 IMU作为另一组（包括17个属性）；而IDS数据集则选取前12个连续属性为一组，其余连续属性为另一组。

5.4.1 云滴群大小对典型相关系数的影响

本实验设置 25个云端，每个云端的数据选取方式与实验二相同。对于给定的云滴群大小 di，实验重复 30次，每次都重新挑选数据。对每个典型相关系数，其误差定义如式(13)所示。取各次所得典型相关系数误差的算术平均值作为平均误差。

由于BDCCA计算典型相关系数是在云滴群上进行的，而其他CCA方法则在原始大数据上进行，因此当数据总容量固定后，云滴群的规模并不影响ApproxCCA和LS-CCA所得典型相关系数的误差，因为在不同云滴群大小下，rApproxCCA和rLS-CCA为常数。故本实验仅仅考察不同云滴群大小下 BDCCA所得典型相关系数误差的变化情况。

图12为不同云滴群大小下前2个典型相关系数的平均误差。由图12可看出：①随着云滴群规模的增大，前2个典型相关系数的误差均逐渐降低，但当云滴群大小超过150时，其降低趋势趋于平缓。此现象的启发是，适当增大云滴群规模有助于降低典型相关系数的误差，但是当其规模增大到一定程度后，再增加云滴数目对于降低误差的贡献并不大。②当云滴群大小超过100时，相关系数的误差均较小，其值未超过0.2，多数在0.1范围内。此现象从相关性这一侧面揭示了大数据的稀疏价值特性，即大量数据中蕴含的相关性通过少量云滴即得以刻画，这与本文研究的最初设想是一致的。

图12 不同云滴群大小下典型相关系数误差

5.4.2 云端数目的影响

在数据总容量和云滴群大小均给定的情况下，本实验评估云端数目对典型相关系数的精度及运行时间的影响。与 5.4.1节的实验相似，当数据总容量固定后，云端规模也不会影响 ApproxCCA和LS-CCA所得典型相关系数的误差，因此本实验关于典型相关系数误差也仅仅考察BDCCA所得典型相关系数误差随云端数目变化而变化的情况。误差定义如式(13)所示。

云滴群大小设置为100。从数据集PAMAP2和IDS中重复抽取100次数据，每次随机抽取 2 × 105条相邻记录。当云端数目 nci给定后，第i个云端分配的记录数目为其中表示向下取整。实验对不同的云端数目 nci重复 10次。图 13为不同云端数目下第1典型相关系数的平均误差，而图14为不同云端数目下的平均运行时间。

5.4.3 数据容量的影响

本实验考察数据总容量对BDCCA所得典型相关系数的精度和运行时间的影响。从数据集PAMAP2和IDS中重复抽取若干次数据，每次随机抽取 1 × 105条相邻记录，直至所取数据达到所需容量 nD为止。共进行10组实验，云端数目设置为，即每个云端分配 1 × 106条记录。云滴群大小设置为100。每组实验重复10次，取每次所得典型相关系数误差的平均值作为输出误差，而取所有云端的最大运行时间作为 BDCCA的运行时间。

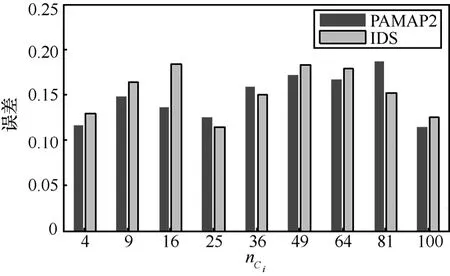
图13 不同云端数目下典型相关系数的误差

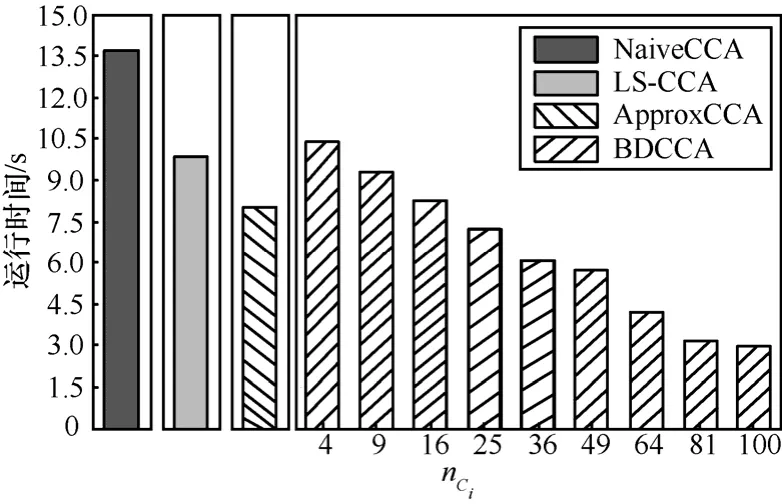
图14 不同云端数目下的平均运行时间

表1为不同总数据容量下前2个典型相关系数的平均误差。误差定义如式(13)所示。由表1可知：1）从总体上看，BDCCA、ApproxCCA和LS-CCA对应典型相关系数误差都随着数据总容量的增加而上升，但后两者是持续地快速上升，且上升幅度较大，而BDCCA在上升过程中存在波动，且上升幅度略小；2）当数据总容量较小时，BDCCA对应典型相关系数误差略大于 ApproxCCA和 LS-CCA对应误差，而当数据总容量较大时，后两者对应误差迅速超过前者对应误差（见表中粗体）。上述现象表明，在数据容量较大的情况下，BDCCA所得典型相关系数精度相对略高，从这个意义上说，BDCCA用于大数据分析是适宜的。

表1 不同数据容量下典型相关系数平均误差

图 15为不同容量下的平均运行时间。由图15可见，BDCCA的平均运行时间并未因数据容量的增大而显著增加，但 ApproxCCA、LS-CCA和NaiveCCA的平均运行时间则随着数据容量的增加而呈线性递增趋势。此现象表明，如果数据容量增大时对等地增加云端数目，则BDCCA能获得较快的处理速度，这恰是大数据的巨大规模特性所欢迎的。

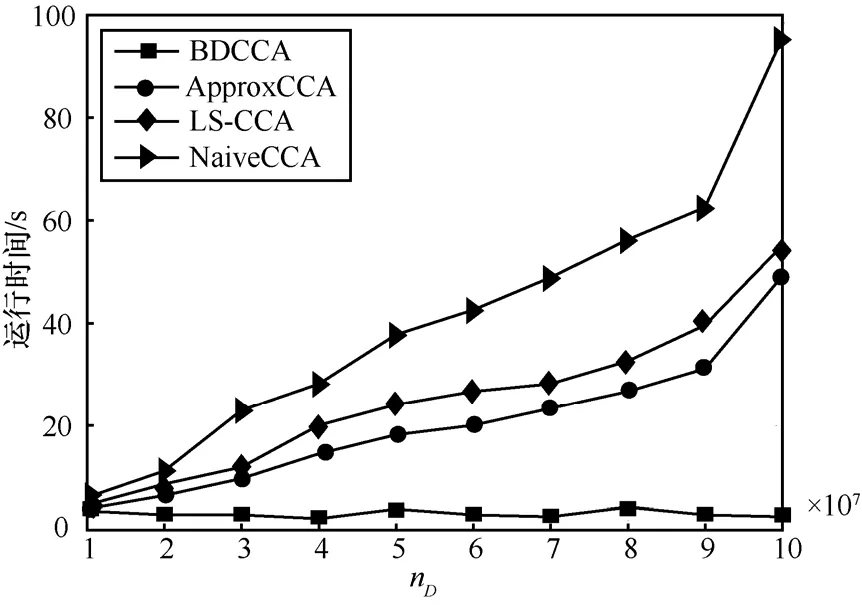
图15 不同数据总容量下平均运行时间

总之，上述实验结果表明，基于所设计的大数据分布式云架构所提出的BDCCA以增加系统资源（即云端）为代价，可获得一定的计算精度和较快的处理速度，这对于大数据快速处理是适宜的。

6 结束语

本文提出了一种面向大数据的CCA方法BDCCA。该方法在容量较小的中心云滴群上进行CCA操作，提高了大数据 CCA的执行效率。为了快速产生中心云滴，首先设计了一种面向大数据挖掘的分布式云架构，为本文大数据存储和计算建立了研究基础；其次重点对多维逆向正态云发生器进行改进，以提高其在大数据环境下产生云的效率；提出了一种一次性合并多个多维云的云合并运算方法，以加快云合并速度。在真实数据集上的实验结果验证了本文方法的合理性和有效性，一方面该方法以增加系统资源（即云端）为代价，可获得一定的计算精度和较快的处理速度；另一方面该方法从相关性这一侧面揭示了大数据的稀疏价值特性。本研究可用于大数据特征融合、机器学习和数据降维等领域。

[1] MINNESOTA M. Big data： science in the petabyte era[J]. Nature,2008, 455(7209)：1-136.

[2] SAKAR C O, KURSUN O. A method for combining mutual information and canonical correlation analysis： predictive mutual information and its use in feature selection[J]. Expert Systems with Applications,2012, 39(3)：3333-3344.

[3] OLCAY K, ETHEM A, OLEG V, et al. Canonical correlation analysis using within-class coupling[J]. Pattern Recognition Letters, 2011, 32(2)：134-144.

[4] KAMALIKA C, SHAM M K, KAREN L, et al. Multi-view clustering via canonical correlation analysis[A]. Proc of the 26th International Conference on Machine Learning[C]. New York, ACM, USA, 2009.129-136.

[5] 杨静, 李文平, 张健沛. 基于秩 2更新的多维数据流典型相关跟踪算法[J]. 电子学报, 2012, 40(9)：1765-1774.YANG J, LI W P, ZHANG J P. A tracking algorithm based on rank two modifications for canonical correlation analysis of multidimensional data streams[J]. Acta Electronica Sinica, 2012, 40(9)：1765-1774.

[6] 顾鑫, 徐正全, 刘进. 基于云理论的可信研究及展望[J]. 通信学报,2011, 32(7)：176-181.GU X, XU Z Q, LIU J. Review of cloud based trust model[J]. Journal on Communications, 2011, 32(7)：176-181.

[7] 黄海生, 王汝传. 基于隶属云理论的主观信任评估模型研究[J]. 通信学报, 2008,29(4)：13-19.HUANG H S, WANG R C. Subjective trust evaluation model based on membership cloud theory[J]. Journal on Communications, 2008, 29(4)： 13-19.

[8] 蒋嵘, 李德毅. 基于形态表示的时间序列相似性搜索[J]. 计算机研究与发展, 2000, 37(5)：601-608.JIANG R, LI D Y. Similarity search based on shape representation in time-series data sets[J]. Journal of Computer Research & Development,2000, 37(5)：601-608.

[9] 许凯, 秦昆, 黄伯和等. 基于云模型的图像区域分割方法[J]. 中国图象图形学报, 2010, 15(5)：757-763.XU K, QIN K, HUANG B H, et al. A new method of region based on image segmentation based on cloud model[J]. Journal of Image and Grphics, 2010, 15(5)：757-763.

[10] HOTELLING H. Relations between two sets of variates[J]. Biometrika, 1936, 28(3)：321-377.

[11] 彭岩, 张道强. 半监督典型相关分析算法[J]. 软件学报, 2008,19(11)：2822-2832.PENG Y, ZHANG D Q. Semi-supervised canonical correlation analysis algorithm[J]. Journal of Software, 2008, 19(11)：2822-2832.

[12] 顾晶晶, 陈松灿, 庄毅. 用局部保持典型相关分析定位无线传感器网络节点[J]. 软件学报, 2010, 21(11)：2883-2891.GU J J, CHEN S C, ZHUANG Y. Localization in wireless sensor network using locality preserving canonical correlation analysis[J]. Journal of Software, 2010, 21(11)：2883-2891.

[13] LI D Y, HAN J W. Knowledge representation and discovery based on linguistic atoms[J]. Knowledge-based Systems, 1998, 7(10)：431-440.

[14] PHILIP R. Big Data Analytics[R]. TDWI Best Parctices Report, 2011.1-38.

[15] BENJAMIN H B, MARK R B, KEITH A S, et al. Large-scale electrophysiology： acquisition, comprression, encryption, and storage of big data[J]. Journal of Neurosience Methods, 2009, 180(1)：185-192.

[16] ARONOVA E, BAKER K, ORESKES N. Big science and big data in biology： from the international geophysical year through the international biological program to the long term ecological research (LTER) network[J].Historical Studies in the Natural Sciences, 2010, 40(8)： 183-224.

[17] WERNER C. Scientif i c perspectivism： a philosopher of science’s response to the challenge of big data biology[J]. Studies in History and Philosophy of Biological and Biomedical Sciences, 2012, 43(1)：69-80.

[18] ALFREDO C, YEOL S, KAREN C D. Analytics over largescale multidimensional data： the big data revolution[A]. Proc of the DOLAP’11[C]. Glasgow, 2011. 101-103.

[19] STEVEN C H H, WANG J L, ZHAO P L, et al. Online feature selection for mining big data[A]. Proc of the Big-Mine’12[C]. New York：ACM, USA, 2012. 93-100.

[20] SIMON B, DUODUO L. On clusterization of ''big data'' streams[A].Proc of the 3rd International Conference on Computing for Geospatial Research and Applications[C]. New York：ACM, USA, 2012.1-6.

[21] JOHN L. Parallel machine learning on big data[J]. XRDS, 2012, 19(1)：60-62.

[22] THOMAS C, PEGGY H, MELANIE M, et al. Building a big data research program at a small university[J]. JCSC, 2012, 28(2)：95-102.

[23] YU C, CHENG J Q, FLORIN R. GLADE： big data analytics made easy[A]. Proc of the SIGMOD’12[C]. New York： ACM, USA, 2012.697-700.

[24] KYUSEOK S. MapReduce algorithms for big data analysis[A]. Proc of the 38th International Conference on Very Large Data Bases (VLDB)[C].New York： ACM, USA, 2012. 2016-2017.

[25] JENS D, JORGE A. Efficient big data processing in hadoop MapReduce[A]. Proc of the 38th International Conference on Very Large Data Bases(VLDB)[C]. New York： USA, ACM, 2012. 2014-2015.

[26] DIVYAKANT A, SUDIPTO D, AMR E A. Big data and cloud computing： current state and future opportunities[A]. Proc of the EDBT 2011[C]. New York： ACM, USA, 2011. 530-533.

[27] XU H Q, LI Z, GUO S M, et al. CloudVista： interactive and economical visual cluster analysis for big data in the cloud[A]. Proc of the 38th International Conference on very Large Data Bases(VLDB)[C]. New York： USA, ACM, 2012. 1886-1889.

[28] COLIN T, DIGITAL P. Big data security[J]. Network Security, 2012,7(2)：5-8.

[29] SOTIRIS K. Combining bagging, boosting, rotation forest and random subspace methods[J]. Artificial Intelligence Review, 2011, 35(3)：223-240.

[30] 李德毅, 杜鷁. 不确定性人工智能[M]. 北京： 国防工业出版社,2005. 224-227.LI D Y, DU Y. Artificial Intelligence with Uncertainty[M]. Beijing：National Defence Industry Press, 2005. 224-227.

[31] TAVALLAEE M, BAGHERI E, LU W, et al. A detailed analysis of the KDD CUP 99 data set[A]. Proc of the Second IEEE International Conference on Computational Intelligence for Security and Defense Applications[C]. Ottawa, Canada, 2009. 53-58.

[32] WANG Y L, ZHANG G X, QIAN J B. ApproxCCA： an approximate correlation analysis algorithm for multidimensional data streams[J].Knowledge-Based Systems, 2011, 24(7)：952-962.

[33] SUN L, JI S W. Canonical correlation analysis for multilabel classification： a least-squares formulation, extensions, and analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011,33(1)：194-200.