在Grassmann流形上构造非相干酉空时码

符达伟，彭立，王利娇，彭秋平

（华中科技大学 电信系 武汉国家光电实验室，湖北 武汉 430074）

1 引言

多发射和多接收（MIMO）无线通信系统可分为相干通信和非相干通信2种方式，与之相对应的有相干空时码（CSTC）和非相干空时码（NSTC）。CSTC已经进入了工业标准，而NSTC目前仍处于研究阶段。众所周知，相干通信需要接收端确切的知道信道状态信息，通常采用的方法是发射端发射接收端已知的导频信号，接收端根据接收的导频信号来估计信道状态信息。显然，导频信号会消耗信道带宽，信道估计会增加解调器的延迟，这些缺陷阻碍了相干通信在高速移动的快衰落信道上的应用。非相干通信是根据非相干空时码的结构特征进行解调的，它不需要发送导频信号，也不必进行信道估计，延迟较小，有可能在未来的高速移动通信中获得应用。

NSTC分为差分空时码[1]和一般酉空时码[2]。Marzetta和Hochwald在1999年提出了非相干空时码的设计准则[3]，并得出一个重要结论：逼近容量限的NSTC具有酉矩阵的结构形式。本文主要研究一般酉空时码的结构设计。目前关于酉空时码的结构设计成果并不多，已经发表的结构设计包括：系统设计[4]、正交设计[5]和基于三角函数的酉空时星座图[6]，这些酉空时星座图的优势是具有代数结构特征，已知一个星座点，通过计算能够得到整个星座图，缺陷是没有采用优化方法设计，不能确定性能是否最优。ZHENG等人解决了非相干通信系统的信息论问题，给出了NSTC的信道容量，它的另一个重要贡献是将Grassmann流形这一数学工具引入到NSTC的研究中，认为酉空时星座图的每一个星座点对应于Grassmann流形上的一个点，故非相干酉空时星座图的设计方法等效于在Grassmann流形上寻找点的最优包络（packings）分布[7]。在此之后，KAMMOUN提出了基于指数映射的Grassmannian酉空时码，由于涉及到指数映射，构造方法较复杂，此外，没有进行优化设计，因此性能也不是最优的[8]。

CONWAYGE和HARDIN从纯数学的角度给出了Grassmann流形上最优包络分布，但它没有采用Frobenius弦距离，而是采用其他形式的弦距离和地测距离，所搜索到的最优包络结果并不能直接成为酉空时码[9]。文献[10]证明了Frobenius弦距离是设计Grassmann流形上非相干酉空时星座图的最佳距离度量准则，并用贪心算法搜索酉空时星座图，由于贪心算法的局部最优特征只能提供次优的搜索结果；于是提出的改进措施是采用直接设计和旋转设计，它们的特点是两阶段设计策略。本文提出改进方案不是在搜索算法上挖掘潜力，而是在信号矩阵的结构上寻找突破点，提出基于Grassmann流形的酉空时矩阵框架结构。算法设计的基本原理是：根据数学领域已经有的Grassmann流形上的最优包络研究成果，设定 Frobenius弦距离阈值，在Grassmann流形上寻找满足酉空时码结构约束的酉矩阵（星座点），大于阈值的点被保留，小于阈值的点被丢弃。仿真实验表明在酉空时矩阵框架约束下，通过设置最优阈值的方法所搜索到的酉空时星座图的性能优于现有酉空时码星座图的性能。

2 系统模型和信号模型

2.1 信道模型

本文采用瑞利平坦衰落信道[1～3]。M 根发射天线，N根接收天线，发射符号间隔为T，在一个T间隔内，信道衰落系数维持不变，从一个T间隔到另一个T间隔，信道衰落参数将随之改变，有些文献也称该信道为准静态瑞利衰落信道[12]。在文献[7]和文献[10]中分析得出：为了在高信噪比下酉空时通信可以达到信道容量，发射符号间隔T必须满足T ≥ min ｛ M , N ｝ +N，当给定M和N后，非相干信道的容量会随着T的增加与相干信道接近；在给定N和T的条件下，为了获得最大的通信自由度，发射天线数目M必须满足设发射信号为（文献[2]称为酉空时调制（USTM）），其中，Φl是一个T×M的酉矩阵。设Y表示接收信号矩阵，由此得到系统模型为

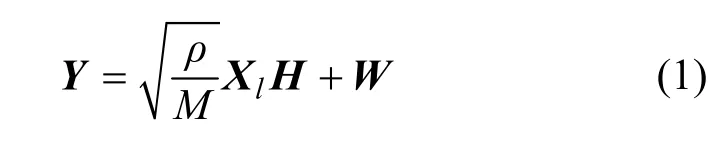
其中，H是M×N维的信道衰落系数矩阵，W是T×N维的加性高斯白噪声（AWGN）矩阵，H和W中的所有元素都是独立同分布的随机变量，服从CN （ 0,1）分布，ρ代表每根接收天线处的信噪比（SNR），归一化系数能保证每根接收天线的平均信噪比是ρ。

接收端采用最大似然解调[2]，其解调表达式为

其中，Tr(⋅)表示矩阵的迹运算，(⋅)†表示复共轭转置。从式(2)可以看出，接收端根据发射信号星座图和接收信号Y，就能进行最大似然解调，不需要进行信道估计。

2.2 Grassmann流形上的酉矩阵框架

设 GT,M表示Grassmann流形，是T维复欧式空间CT上所有M维子空间的集合，它也构成一个齐次空间，与正交群的商空间 O ( T ) /(O( M ) × O ( T -M))或酉群的商空间 U ( T ) (U( M ) × U ( T - M ))同构，因此，GT,M上所有T×M维的酉矩阵构成等效类，或者说 GT,M可用一个酉矩阵来表示。

定义1 (Grassmann流形上非相干酉空时码矩阵框架)：设矩阵Φ ∈ GT,M，其中，T表示相干时间间隔，M表示发射天线数， φij∈ C (i = 1 ,…,T,j = 1 ,… ,M )表示Φ中的元素，如果构造矩阵

满足以下3个条件。

1)Φ†Φ = IM，其中， IM为M维的单位矩阵。

2)Φ中元素的自由度为 d imΦ(GT,M)=M(TM )，表示Φ的TM个复元素中有 M ( T - M )个复元素是独立的，余下 T M - M ( T - M ) = M2个元素可由独立的 M ( T - M )个元素确定。

3) φij≠0， i = 1 ,… ,T , j = 1,…,M ，则称Φ 是基于Grassmann流形的酉空时码矩阵框架。

如果将复元素φij看成广义的QAM调制符号，那么式(3)的酉矩阵Φ实际上是对任意复数的调制符号φij∈C进行空时编码。由于定义 1只给出了酉空时矩阵Φ的部分信息，如维数T×M和矩阵的某种结构关系（酉矩阵结构和元素独立约束），但没有给出每个元素φij的值，因此称Φ为发射信号星座图的矩阵框架。 L =2RT由式(3)确定的Φl矩阵构成Grassmann流形上的酉空时信号星座图，编码速率为R =(lbL)/T(bit/s/Hz)。对于Φl中所有元素φij∈ C (i = 1 ,… , T , j = 1,… ,M )，当 φij≠ 0时，酉空时调制保证给出满发射；当某个 φij= 0时，表示第j∈[1,M ]根天线在第i∈[1,T]个时刻没有发射信号，发射端不能形成满发射分集。初步观察可以发现：如果发射的酉矩阵Φ的所有元素均不为零，那么空时码一定能达到最大分集增益和最大编码增益（反之，不一定成立）。因此，本文的主要任务是在 Grassmann流形上寻找最优分布的，使所有Φl满足定义1中的3个条件。

2.3 距离测度

于是，本文定义的最优包络问题描述如下：给定L、T、M，在酉矩阵框架(3)的约束条件下，寻找集合，使尽可能得大。

在文献[9]中，研究了Grassmann流形上的最优包络问题，采用与式(4)不同的距离测度，给出了L= 2 ～50的最优包络搜索结果，如 L = 1 6的最优包络给出的弦距离为=1（这里 dc不是Frobenius弦距离）， L = 1 8的最优包络构成正多边形，边长为 dc= 1 ，但所得到的最优包络不能很好地充当空时码，因为搜索到的任意中，可能存在一定数量 φij= 0 的情况，使空时码的编码增益和分集增益有所损失。文献[10]研究以 4为测度，利用贪心算法、直接设计和旋转设计等方法寻找的最优分布问题，由于没有给出类似于定义1的框架约束条件，所得到的最优并不是在Grassmann流形上的点，并且寻找最优分布的搜索工作存在下列 2个问题：1）能够搜索到的次优或最优分布，但不一定是最优空时码，出现与文献[9]一样的情况；2）在未加约束的任意范围内搜索，可能找到最优分布，但搜索工作的计算量相当大。本文引入满足酉矩阵条件1）、Grassmann流形的参数条件 2）和空时码条件 3）的框架约束，不仅能找到Grassmann流形上的最优包络，也能保证在满分集增益和满编码增益条件下，搜索到距离特性最优的酉空时码星座图。

3 在G4,2上非相干酉空时码设计

3.1 在G4,2上的酉空时码矩阵框架重构

蛮力搜索式(3)的Φ矩阵是很困难的，可以根据元素间存在的相互关系，对Φ进行重组。重组方案有2种，一种是将Φ矩阵看成M个列矢量，可以在矢量空间中寻找M个彼此标准正交的列矢量构成的T×M维Φ矩阵，并由此寻找L个Φ矩阵构成相应的星座图，关于这个方法的论述见文献[9]；另一种是本文讨论的将Φ矩阵按列分成K个子块，即当T = KM，K为任意大于等于2的正整数，要求每个分块子矩阵都是一个M×M的方阵，故Φ可以表示为表示矩阵转置。有

为了便于展示本文所提出的构造星座图方法的过程和性能，给出了发射时间间隔为 4T= ，发射天线和接收天线均为2(即 2K= )条件下的星座图构造(T和M的选取满足 3.1节中的约定，且T KM= ，K为常数)。根据定义1的框架结构，本节给出Grassmann流形4,2G 上酉空时码星座图的设计方法。根据式(5)，可将搜索自由度为4的42×矩阵简化为搜索2个22×子矩阵，其中每个子矩阵的自由度为2。设1φ和2φ是自由度为2的一个22×酉矩阵中的2个复元素，且1φ和2φ相互独立。如果允许每个复元素能进行乘-1、乘和共轭操作，那么1φ和2φ在22×的酉矩阵中的分布会有许多排列方案，下面是几种排列的例子：

可任取其一作为Φ4×2矩阵的子矩阵，为了简单起见，假设取Φ1=，那么Φ2与Φ1有相同的结构：

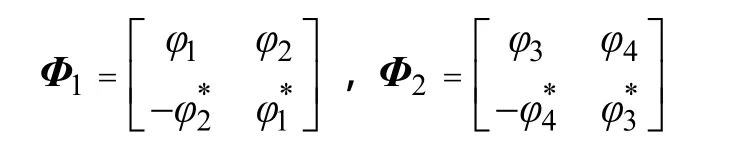
其中，φ1, φ2, φ3, φ4相互独立。考虑对列矢量的归一化，得到Grassmann流形 G4,2上的酉空时码矩阵框架为

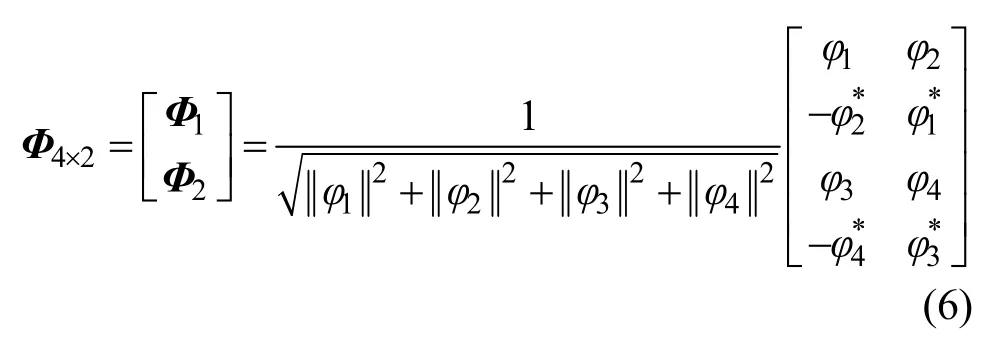
φi（ i = 1 ,2,3,4）可以表示成幅值A和辐角θ的极坐标形式，即 φi= Aiejθi，i = 1 ,2,3,4，j为虚数单位。由此可得在 T = 2 M = 4时基于QAM调制符号的酉空时编码矩阵

记式(7)为G4,2上酉空时码矩阵框架，称在该框架下构造的星座图为G4,2-QAM酉空时星座图。余下的问题是在 G4,2上寻找最优包络，以便确定Ai和θi，i= 1 ,2,3,4。

3.2 在G4,2上酉空时星座图的优化搜索

对于 L = 1 6， T = 2 M = 4，构造Grassmann流形 G4,2上最优星座图的问题等效于下列优化问题。即寻找满足矩阵框架(7)的Ai和θi(i=1,2,3,4)，使尽可能大。G4,2可看成 R4空间的一个球[9]，由式(7)构成的酉矩阵集合是球上的点，这个球的半径是1，球上位于直径两端的点称为对跖点，对跖点之间的距离是2，也是球上任意两点的最远距离(即球的直径)。设QΦ表示T维复空间的M维子空间，QΦ⊥是QΦ的补空间，该补空间内的点也是 Grassmann流形上的点，实际上Φ∈QΦ和是Grassmann流形上的对跖点。

优化搜索算法描述如下：设{Φ}表示一个空集，选择一个初始点 ( Φ4×2)1放入集合{Φ}中，计算(Φ4×2)1的对跖点，将也放入{Φ}中。根据式(7)构造一个4×2的(Φ4×2)l矩阵，具体做法是设置变化的步长为a，θi变化的步长为b，由于Ai不能为0（因为 φij≠0），所以Ai的取值范围为[a,1]，θi的取值范围为[0,2π]。在步长a和b的控制下，选取4个复数值 φ = A e jθi， i = 1 ,2,3,4，构成形如式(7)

i i的酉矩阵(Φ4×2)l，计算(Φ4×2)l与集合{Φ}中所有已有星座点的Frobenius弦距离，如果所有距离值均大于事先确定的距离阈值dth，那么将(Φ4×2)l保留在集合{Φ}中，如果所计算出的距离值中有一个小于dth，则放弃这个(Φ4×2)l。继续修改Ai和θi值，生成新的(Φ4×2)l，重复上述过程，直到集合{Φ}中的元素个数为 L = 1 6，则完成星座图的设计。

对上述算法有如下几点说明。

1) 初始点 (Φ4×2)1的选取可以是任意满足式(7)的酉矩阵，为简单起见，本文规定 Ai= 1 和 θi=0,i= 1 ,2,3,4，即可得到 ( Φ4×2)1，设它的对跖点为(Φ4×2)1和中的列矢量存在彼此正交的关系，它们的结构如下

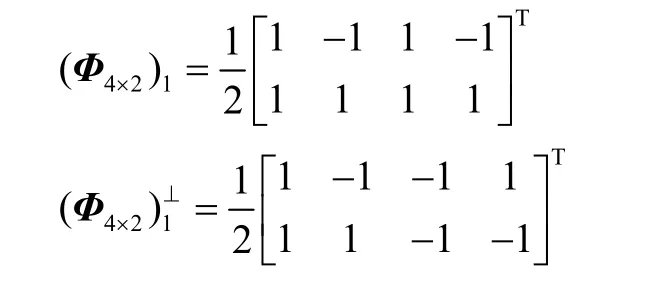
2) 步长a的选择可以是(0,1]之间的任意值，取a = 1 /m，m是正整数，步长b的选择可以是[0,2π]任意值，取 b = 2 π/n，n是正整数。则候选矩阵的个数为，由此可以看出，m和n的取值决定了上述搜索算法的复杂度。显然，步长a和b的取值越小，步长的倍数值m和n的取值越大，等待候选的矩阵个数就越多，搜索计算量就越大。例如，当 m = 4 ， n = 4 ， a = 0 .25， b =π/2时，候选点的数量为上述搜索算法的一个简化方案 Ai是：只需搜索7个点，然后求它们的对跖点。

3) 距离阈值 dth的选取根据实际情况确定。根据文献[9]提供的 Grassmann流形 G4,2上的最优包络搜索结果，对于 L = 1 6的最优包络，几何弦距离的最小值为1，所对应的最小Frobenius弦距离初步估计略大于0.8，所以取 dth= 0 .8。这16个星座点的Frobenius弦距离分布如图1所示。在G4,2-QAM酉空时星座图集合中，到初始点 (Φ4×2)1的Frobenius弦距离为1.082 4的酉矩阵有2个，弦距离为0.808 3的酉矩阵有6个，弦距离为1.345 0的酉矩阵有6个，弦距离为 2。0的酉矩阵有 1个。在这个星座图中，成对最小Frobenius弦距离为0.808 3。

4 仿真与结果分析

非相干酉空时码的实际应用需要考虑与二进制信息序列之间的映射关系，即给星座图中每一个点分配一个二进制序列作为该点的标识，对于星座图需要给每个点分配 nb= lb(L) = 4bit的二进制序列。由图1的距离分布可以看出，星座图点之间的距离并不是一致的，距离相近的点发生解调错误的概率较大，若把 Frobenius距离相近的星座图点分配汉明距离相近的二进制序列，这显然可以改善误码性能，这种映射规则就是准格雷映射。本文采用文献[11]中介绍的准格雷映射算法完成从二进制序列到G4,2-QAM星座图的映射。

图1 15个G4,2-QAM酉空时码字到初始点的Frobenius弦距离分布

在天线数目 M = N= 2 、相干时间 T = 2 M =4和星座图尺寸 L = 1 6（或数据速率 R = 1 bit/s/Hz）的条件下，图2给出了本文提出的G4,2-QAM非相干酉空时码与某些现有非相干酉空时码的性能比较曲线。这些现有非相干空时码包括：文献[4]的基于计算机搜索的系统设计酉空时码、文献[5]的正交设计的酉空时码和文献[6]的基于三角函数的酉空时码。图2的仿真结果表明，在误码率为 1 0-5数量级时，本文提出的方案比正交设计的酉空时码性能改善1 dB，比系统设计的酉空时码性能改善2.1 dB，比基于三角函数的酉空时码性能改善8 dB。

图2 G4,2-QAM空时码与某些已有酉空时码的性能比较

图 3给出的是本文构造的酉空时码与文献[8]中同在Grassmann流形下用指数映射方法构成的酉空时码的性能比较，容易看出G4,2-QAM非相干酉空时码比基于指数映射Grassmann酉空时码性能改善2dB。这种性能的改善得益于在框架结构约束下Grassmann流形上最优包络点的搜索结果。

图3 G4,2-QAM空时码与基于指数映射Grassmann酉空时码的性能比较

图4是在本文设计方法基础下星座图大小分别为16和32点的星座图的性能比较，可以看到16点星座图码的性能优于 32点星座图码，但其传输速率低于32点的酉空时码星座图，32点星座图的编码速率为 1.25R= bit/s/Hz。

图4 G4,2-QAM空时码16点和32点星座图的性能比较

5 结束语

本文设计了一种新的具有潜在实用价值的Grassmannian非相干酉空时码星座图，它是目前在Grassmann流形上所构造出来的最优非相干酉空时码星座图，其仿真性能也优于非Grassmann流形上非相干酉空时码星座图的性能。用Grassmann流形这一数学工具来研究非相干酉空时码的理论问题的研究成果较多，但提出实用酉空时码结构的应用研究一直进展缓慢，本文所提出的酉矩阵框架结构，给出了非相干酉空时码的在Grassmann流形上的实用模型，并使Grassmannian星座图的搜索算法比现有的遍历搜索算法具有更低的计算复杂度。未来的研究工作是构造有利于降低最大似然解调算法计算复杂度的Grassmannian非相干酉空时星座图。

[1] TAROKH V, JAFARKNANI H. A differential detection scheme for transmit diversity[J]. IEEE Journal on Selected Areas in Communications, 2000, 18(7)：1169-1174.

[2] HOCHWALD B M, MARZETTA T L. Unitary space-time modulation for multiple antenna communication in Rayleigh flat fading[J]. IEEE Trans Inform Theory, 2000, 46(2)：543-564.

[3] MARZETTA T L, HOCHWALD B M. Capacity of a mobile multiple-antenna communication link in Rayleigh flat fading[J]. IEEE Trans Inform Theory, 1999, 45(1)：139-157.

[4] HOCHWALD B M, MARZETTA T L, RICHARDSON T J. Systematic design of unitary space-time constellations[J]. IEEE Trans Inform Theory 2000, 46(6)：1962-1973.

[5] ZHAO W, LEUS G, GIANNAKIS G B. Orthogonal design of unitary constellations for uncoded and trellis-coded noncoherent space-time systems[J]. IEEE Trans Inform Theory, 2004, 50(6)：1319-1327.

[6] TAROKH V, KIM I M. Existence and construction of noncoherent unitary space time codes[J]. IEEE Trans Inform Theory, 2002, 48(12)：3112-3117.

[7] ZHENG L, TSE D N C. Communication on the Grassmann manifold：a geometric approach to the noncoherent multiple-antenna channel[J].IEEE Trans Inform Theory, 2002, 48(2)：359-383.

[8] KAMMOUN I, CIPRIANO A M, BELFIORE J C. Noncoherent codes over the Grassmannian[J]. IEEE Trans Wireless Commun, 2007,6(10)：3657- 3667.

[9] CONWAY J H, HARDIN R H, SLOANE N J A. Packing lines, planes,etc.： packings in Grassmannian spaces[J]. Experimental Mathematics,1996, 5(2)：139-159.

[10] GOHARY R H, DAVIDSON T N. Noncoherent MIMO communication： Grassmannian constellations and efficient detection[J]. IEEE Trans Inform Theory, Mar. 2009, 55(3)：1176-1205.

[11] COLMAN W K, GOHARY R H, EI-AZIZY M A, et al. Quasi-gray lablling for Grassmanian constellations[J]. IEEE Wireless Communications, 2011, 10(2)：626-636.

[12] KAMMOUN I, BELFIORE J C. A new family of Grassmannian space-time codes for noncoherent MIMO systems[J]. IEEE Communication Letters, 2003, 7(11)：528-530.