关于拟α-半交换环
2013-10-28张培雨丁婷婷
张培雨,吴 俊,丁婷婷
(安徽师范大学数学与计算机科学学院,安徽 芜湖 241000)
关于拟α-半交换环
张培雨,吴 俊,丁婷婷
(安徽师范大学数学与计算机科学学院,安徽 芜湖 241000)
文章引进了拟α-半交换环的概念,它是α-半交换环和弱半交换环的推广.给出了它的一些刻画以及与α-半交换环和拟α-半交换环的关系.
α-rigid环;弱半交换环;α-半交换环;拟α-半交换环;Armendariz环
0 引 言
本文中无特别说明所有的环均指有单位元的结合环,其中N(R)是指环R的所有幂零元,Tn(R)是指环R的n阶上三角矩阵环.称α是环R的自同态,若对任意的a,b∈R,有α(a+b)=α(a)+α(b);α(ab)=α(a)α(b).本文若无特别说明α均不是零同态和恒等同态.称R是半交换环,若ab=0,则aRb=0.称R的自同态α是rigid的[1],若a∈R,aα(a)=0,则a=0.称R是α-rigid环[2],若R存在一个rigid自同态α.
近年来有许多学者对半交换环做了相应的研究.在文[3]中Liang Li等人引入和讨论了弱半交换环.环R称为弱半交换环[4],若ab=0,则对任意r∈R,arb∈N(R).在文[5]中Muhittin Baster等人提出了α-半交换环的概念并研究了它的相关性质.称R是α-半交换环[5],若ab=0,则aRα(b)=0.本文推广了α-半交换环,弱半交换环的概念,引进了拟α-半交换环的概念,并给出了它们之间的关系和相应的性质研究.
1 拟α-半交换环与α-半交换环,弱半交换环
定义1设α是R的自同态,称R是拟α-半交换环,若ab=0,则对任意r∈R,有arα(b)∈N(R).
由定义可知,α-半交换环一定是拟α-半交换环.下面例子说明反之是不成立的,因此拟α-半交换环是α-半交换环的真推广.


由于F是域,则a11c11b11=0=a22c22b22,(ACα(B))2=0,因此R是拟α-半交换环.
□
命题1设R是约化环,α是R的自同态,则下列命题等价:
(1)R是α-半交换环;
(2)R是拟α-半交换环.
证明:只需证(2)⟹(1)若a,b∈R,且ab=0,由于R是拟α-半交换环,则对任意r∈R,有arα(b)∈N(R),又由于R是约化环,则arα(b)=0,因此得证.
□
设R是拟α-半交换环,当α是恒等同态时,则R是弱半交换环.下面的例子说明了,对于R的任意自同态α,若R是弱半交换环,则R不一定是拟α-半交换环.

□
设R是环,α是R的自同态,称R满足α-条件,若ab=0⟺aα(b)=0.
引理1[3,引理3.1] 设R满足α-条件,a,b∈R,若ab∈N(R),则aα(b)∈N(R).
□
命题2设R是弱半交换环,若R满足α-条件,则R是拟α-半交换环.
证明:令a,b∈R,若ab=0,由于R是弱半交换环,则对任意的r∈R,有arb∈N(R),由引理2.5知,arα(b)∈N(R),故R是拟α-半交换环.
□
由例2和下面的例子说明弱半交换环与拟α-半交换环之间没有必然的联系.

□
2 拟α-半交换环



□


□
推论1[3,命题3.2] 设R是环,I是R的理想,且R/I是弱半交换环,若I⊆N(R),则R是弱半交换环.
□
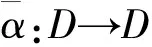
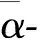
证明:令(r1,s1),(r2,s2)∈D,若(r1,s1)(r2,s2)=0即r1r2+s1r2+s2r1=0,s1s2=0,由于S是整环,故s1=0或s2=0.若s1=0,则0=r1r2+s1r2+s2r1=r1(r2+s2),由于R是拟α-半交换环且α(1)=1,则对任意t∈R,
r1tα(r2+s2)=r1tα(r2)+r1ts2∈N(R).
即存在n∈N,使得(r1tα(r2)+r1ts2)n=0.而对任意的(r,s)∈D,

则取t=r+s,令r1(r+s)α(r2)+r1(r+s)s2=m,由上可知mn=0,所以(m,0)n=0,故
企业各部门制定的各类预算,是财务预算编制的重要凭据。以本公司为例,业务部门的预算为年度预算编制工作开展的基础,收入预算应以该指标为基础进行编制,在以上工作结束后才可对成本费用预算进行编制,成本费用与现金流量预算是企业财务预算工作的总结,而利润表、资产负债表预算为所有预算的综合体现形式。

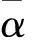
□

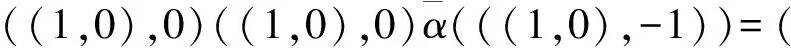
而对任意的n∈N,((-1,0),0)n=(((-1)n,0),0)≠0.
注:由例4可知,命题5中的α(1)=1该条件不可忽略.
推论2若R是弱半交换环,S是整环,则R通过S的Dorroh扩张是弱半交换环.
□

(1)R是拟α-半交换环;
(2)R[x]是拟α-半交换环;
(3)R[x;x-1]是拟α-半交换环.

(2)⟹(3)由于R[x]是拟α-半交换环,令f(x),g(x)∈R[x;x-1],且f(x)g(x)=0,则存在n∈N,使得f1(x)=f(x)xn,g1(x)=g(x)xn∈R[x],从而f1(x)g1(x)=0,所以f1(x)R[x]α(g1(x))⊆N(R[x]).对任意h(x)∈R[x;x-1],存在m∈N,使得h1(x)=h(x)xm∈R[x],则存在s∈N,使得(f1(x)h1(x)α(g1(x)))s=0,而
f(x)h(x)α(g(x))=f1(x)x-nh1(x)x-mα(g1(x)x-n)=f1(x)h1(x)α(g1(x))x-2n-m.
故
(f(x)h(x)α(g(x)))s=(f1(x)h1(x)α(g1(x))x-2n-m)s=(f1(x)h1(x)α(g1(x))sx(-2n-m)s=0.
故R[x]是拟α-半交换环.
(3)⟹(1)由于R是R[x;x-1]的子环,因此结论成立.
□
推论3[3,推论3.2] 设R是环,R[x]是弱半交换环当且仅当R[x;x-1]是弱半交换环.
□

证明:⟸由于R是Tn(R)的子环,故结论成立.
⟹令


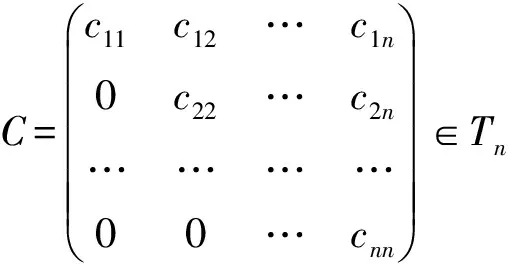
则

由于R是拟α-半交换环,故存在k∈N,使得(aiiciiα(bii))k=0,i=1,2,…,n.故


□
□
推论5设R是环,则R是拟α-半交换环当且仅当R[x]/(xn)是拟α-半交换环.

[1]KrempaJ.Someexamplesofreducedrings[J].AlgebraColloq,1996,3(4):289-300.
[2]HongChanyong,KimNK,KwakTK.Oreextentionsofbaerandp.p.-rings[J].PureandApplAlgebra,2000,151(3):215-226.
[3]LiangLi,WangLimin,LiuZhongkui.Onageneralizationofsemicomnutativerings[J].TaiwaneseJournalOfMathematics,2007,11(5):1359-1368.
[4]MuhittinB,TaiKK.Extendedsemicommutativerings[J].AlgebraColloq,2010,17(2):257-264.
[5]MuhittinB,AbdullahH,TaiKK.Generalizedsemicommutativeringsandtheirextensions[J].BullKoreanMathSoc,2008,45(2):285-297.
[6]AntoineR.NilpotentelementsandArmendarizrings[J].JAlgebra,2008,319(8):3128-3140.
[7]AndersonD,CamilloV.ArmendarizringsandGaussianrings[J].CommAlgebra,1998,26(7):2265-2272.
[8]HongChanyong,KimNK,KwakTK.Extensionsofgeneralizationreducedrings[J].AlgebraColloq,2005,12(2):229-240.
OnQuasiα-SemicommutativeRings
ZHANG Peiyu, WU Jun, DING Tingting
(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)
This paper introduced the notion of quasiα-semicommutative rings which were the generalizations ofα-semicommutative rings and provided some characterizations of quasiα-semicommutative rings as well as the relations withα-semicommutative rings and weakly semicommutative rings.
α- rigid rings; weakly semicommutative rings;α-semicommutative rings; quasiα-semicommutative rings; Armendariz rings
2013-04-04
吴 俊(1964—),男,教授,博士,主要从事同调代数与代数表示论研究.E-mail:wujunanhuiwuhu@gmail.com
10.3969/j.issn.1674-232X.2013.05.005
O153.3MSC201013M05
A
1674-232X(2013)05-0409-04
