太阳能小屋的设计

高华岳,胡 露,冯姗姗,何颖俞

(1.杭州师范大学理学院，浙江 杭州 310036；2.杭州师范大学教育科学学院，浙江 杭州 310036)

太阳能小屋的设计

高华岳1,胡 露2,冯姗姗1,何颖俞1

(1.杭州师范大学理学院，浙江 杭州 310036；2.杭州师范大学教育科学学院，浙江 杭州 310036)

文章针对山西大同市的地理位置和气象数据条件，利用一系列优化方法对规定尺寸的小屋合理铺设光伏电池，进而讨论太阳能小屋的投资收益.得出了架空方式比贴附方式降低投资回收年限，效果更优.同时也设计出了满足一定要求的太阳能小屋，该设计降低了成本，收益却更大.

目标规划；光伏电池；最佳倾角；启发式算法；太阳能小屋设计

开发新能源与可再生清洁能源，是 21 世纪世界经济发展中最具有决定性影响的五项技术领域之一，其中太阳能光伏发电最受瞩目.太阳能是一种取之不尽、用之不竭的能源，利用光伏电池可以将太阳辐射能量转化为电能，这些电能除了供家庭使用外，剩余电量并入电网，因此在房屋的外表面合理地铺设光伏电池对能源利用具有重要作用.大量研究者都致力于光伏电池的安装问题,如刘振宇，冯华，杨仁刚[1]等研究了山西不同地区太阳辐射量以及光伏电池安装的最佳倾角问题；徐丰，王波，张海龙[2]等研究了建筑物日照分析中太阳位置计算公式的改进；张鹤飞[3]研究了与太阳辐射量有关的物理量计算方法.这些研究对不同地区光伏电池安装的倾角，太阳辐射的吸收做了理论上的计算，而对于具体建筑物外表面的铺设并没有涉及.本文的选题为2012年全国大学生数学建模竞赛B题，基于山西大同市的地理位置与气象条件，对所给小屋外表面选择合适的太阳能电池进行合理铺设，使之得到最大效益.

1 贴附式、架空式铺设光伏电池的数学模型与求解

1.1 光伏电池的选择

按照应用需求，太阳能电池经过一定的组合，达到一定的额定输出功率和输出电压的一组光伏电池，叫光伏组件.根据光伏电站大小和规模，光伏组件可组成各种大小不同的阵列.在设计太阳能小屋时，光伏电池在小屋的外表面(屋顶和外墙)的铺设安排是问题关键.其工作原理是：光伏电池组件将产生的直流电，经过逆变器转换成220V交流电后供家庭使用，并将剩余电量输入电网.已知以下条件:(1)不同种类的光伏电池每峰瓦的价格差别很大；(2)每峰瓦的实际发电效率或发电量还受诸多因素的影响：如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式——贴附或架空等；(3)在同一表面采用两种或两种以上类型的光伏电池组件时，同一型号的电池板可串联，而不同型号的电池板不可串联；(4)在不同表面上，即使是相同型号的电池也不能进行串、并联连接,应注意分组连接方式及逆变器的选配.

太阳能光伏电池(简称光伏电池)可把太阳的光能直接转化为电能.目前光伏系统大量使用的是以硅为基底的硅太阳能电池，可分为单晶硅太阳能电池、多晶硅太阳能电池与非晶硅太阳能电池.在能量转换效率和使用寿命等综合性能方面，单晶硅和多晶硅电池优于非晶硅电池.多晶硅比单晶硅转换效率低，但价格更便宜.非晶硅薄膜光伏电池的工艺制造过程与单晶硅和多晶硅相比大大简化，硅材料消耗少, 单位电耗也降低了很多.

通过对3种类型的光伏电池(A单晶硅、B多晶硅、C非晶硅薄膜；每种光伏电池最多选择11个型号)组件设计参数和市场价格分析，可以得到以下参数：

光伏组件的效率，所有光伏组件在0～10年效率按100%，10～25年按照90%折算，25年后按80%折算，因此经过计算35年后得到的总电量相当于效率按100%计算得到的31.5年后的总电量.

通过对山西大同典型气象年逐时参数及各方向辐射强度的数据分析，可以直接得到东、南、西、北4个外表面的总辐射强度，房顶的两个面都有一定的倾角，不能直接用水平面的总辐射强度进行计算，因此需要根据太阳入射角θ和法向直射辐射强度来计算两个屋顶面的总辐射强度.

Btk=bt×cosθ,k=1,2

这里θ为太阳入射角，bt为t时刻的法向直射辐射强度，k=1(朝南屋顶面)，k=2(朝北屋顶面)，k=3(东面)，k=4(南面)，k=5(西面)，k=6(北面).

因此，可以得到各个面不同时刻的总辐射强度，应用光伏电池的光生伏特效应，经一定的转换效率，产生直流电.再通过逆变器将直流电转变成交流电，从而就可以得到每年的发电总量.利用MATLAB软件计算得到3种电池类型不同产品型号在35年内发电总量与单位面积成本，结果如下(只列举部分结果).

表1 电池类型不同产品型号35年内发电总量与单位面积成本

由表1可知光伏电池在北向的发电量极少，因此在下面的讨论中不考虑光伏电池在北向和朝北向屋顶面上的铺设，即只需考虑朝南向屋顶面、东面、南面、西面的光伏电池的铺设优化问题即可. 用光伏电池单位面积的效益来衡量光伏电池的优劣，在这里先不考虑因逆变器带来的成本增加，因此有：光伏电池在第k面单位面积的效益=单位面积所得的经济收入-单位面积的成本，其中电价按0.5元/kWh计算，可以得到：东面可铺设薄膜光伏电池，以C1，C5最佳；南面可铺设多种类型光伏电池，以B3，B5，C1，C5最佳；西面可铺设薄膜型电池，以C1,C5最佳；朝南屋顶面可铺设单晶硅和多晶硅光伏电池，以A3和B3最佳．

1.2 贴附式铺设光伏电池的数学建模与求解

考虑光伏电池在小屋外表面铺设的优化设计，使得小屋的全年太阳能光伏发电总量尽可能大，而单位发电量的费用尽可能小.用Ek来表示35年内光伏电池在第k面单位面积光伏电池的效益(k=1,2,3,4,5,6)，可以建立一个目标规划，如下

x1t=0,当Btk<200,不供电

x1t=1,当Btk≥200,能供电

(1)

Pij，ηij,sij,nij分别为第i种电池类型第j种产品型号的光伏电池的组件功率，转换效率，面积与数量，其中，i=1,2,3；j=1,2,…,11；ci为第i种电池类型的价格，其中，i=1,2,3；Ni，Φi分别为所使用的第i种逆变器的数量与价格.约束条件中

为35年内第i种电池类型第j种产品型号光伏电池在第k面的发电总量,Btk为t时刻第k面的总辐射强度，t=1,2,…,3760，k=1(朝南屋顶面)，k=2(朝北屋顶面)，k=3(东面)，k=4(南面)，k=5(西面)，k=6(北面).并且考虑到其中当光照强度小到一定程度如：当使用A单晶硅电池，辐照强度低于200W/m2时，电池转换效率<转换效率的5%.可以忽略其发电量了，因此，可以引入0-1变量：

另外，x2t,x3t均为1.每个面铺设的光伏电池总面积应小于各个外表面可铺设的面积,即

在已建立的目标规划基础上，利用Lingo软件的编程计算和进一步优化编排，可得到如下结果.

表2 不同朝向墙面的光伏电池数量及串并联方式

下面给出南面和西面电池组件铺设分组阵列图形示意图：

图1 南面及西面电池组件铺设分组阵列图及连接方式Fig. 1 Component grouping array diagram and the connection mode of laying on South and West walls

在上面各个光伏电池的发电量处理中已经将小于最低启动辐射量做了剔除，所以只要考虑电池的35年(等效于100%效率下31.5年)的发电量.同时根据逆变器自身的转化效率，可以得到该光伏电池的发电量，当前民用电价按0.5元/kWh计算，而在计算返本时间中也要将逆电器的成本计算在内.由此可以得到表3.

表3 太阳能小屋的发电量、经济收益以及回报年限

1.3 架空式铺设光伏电池的数学建模与求解

用架空方式来安装光伏电池时，只考虑屋顶面上的光伏电池的架空而不考虑垂直墙面上光伏电池的架空安装.对于屋顶来说，同一时间同一地点同一种光伏电池型号，安装方式不同，则太阳光辐射的入射角也就会改变，因而相对于铺设方案来说，选取光伏电池型号及数量也会发生变化，但对于东南西北四面墙壁来说也就不会发生改变.因此，对于太阳能小屋的最优铺设方案，主要考虑的是屋顶光伏电池铺设的优化.

表4 倾角变化后不同朝向墙面的光伏电池数量及串并联方式

利用启发式算法，考虑大同市的地理位置和气象数据，通过MATLAB程序[4]模拟光伏电池在不同铺设倾角下其一年内接收的总辐射能量.从模拟的结果中可以得到南屋顶上光伏电池的最优铺设倾角为37.6度，那么与上面贴附式铺设光伏电池数学模型建立的方法相同，得到倾角改变后的各种型号光伏电池在朝南屋顶面的单位面积效益，得到效益最大的为采用A3型号的光伏电池铺设方案.

在约束条件不变的情况下，使得采用架空安装后效益Ek最大，则由此同样也可建立目标规划问题(1)，则可得其具体的铺设方案(见表4).

根据以上得出的数据，可以计算各个外表面35年内总发电量、经济效益和回报年限(见表5).结果显示，在屋顶以架空方式铺设电池降低了投资回收年限，为21.5年.这与贴附式铺设光伏电池相比降低了投资回收年限，效益更优.

2 太阳能小屋的设计——模型建立与求解

表5 架空安装后太阳能小屋的发电量、经济收益以及回报年限

5)建筑采光要求至少应满足窗地比(开窗面积与房间地板面积的比值，可不分朝向)≥0.2，即

6)建筑节能要求应满足窗墙比(开窗面积与所在朝向墙面积的比值)南墙≤0.50、东西墙≤0.35、北墙≤0.30，即

考虑到设计太阳能小屋的实用性和美观性，要求南面墙窗比≥0.2。

由以上的目标函数和约束条件，可以建立目标规划问题.但是上述规划问题属于典型的NP-Hard问题，不能从一般的解法得到最优解.同时由于约束条件的复杂性，考虑从其他角度解决该问题.仔细观察这座小屋的布局，利用高科技自动调节控制而实现“零能耗”、“恒温”.考虑尽量不破坏小屋原本布局，在约束条件的要求下，对该房屋进行优化.

(1)向南的屋顶倾角约束.考虑到该地区最适宜的倾角，因此将向阳面的倾角考虑成37.6°,以此使得屋顶的效率最高.

(2)最低墙高度与最高墙高度约束.由于电量基本上来自于屋顶的电池，并且由此约束，求得最大的允许墙落差为2.6 m.然后考虑到屋顶倾角固定，所以可以得到向南屋顶的最大宽度.同时得知屋顶在侧视图水平面上最大投影长为3.37 m.

(3)最小宽度、最大长度、最大投影面积约束.在此约束下，如果要求朝南的屋顶面积最大，那么就要宽度最小，长度最大.经过面积的计算得到房屋投影为以下取值：长15 m、宽4.9 m.

(4)窗地比、窗墙比约束.经过计算，得到窗(包括门)的面积为25.3337 m,所以完全满足窗地比，在拥有足够余量的同时考虑将屋顶的天窗取消，增加屋顶的发电面积.由于墙壁对电量以及效益的贡献小，所以对墙壁上门窗的面积不做处理，使得屋内有足够的采光.同时在此情况下满足窗墙比．

(5)方向角度变化影响.在此模型中，主要考虑了屋顶的发电效能，认为以房屋方位角为0度为效率最大(以正南为正方向)，但是针对当地气象的实际情况，建议对模型进行改进，考虑方位角的变化．

(6)每个面铺设的光伏电池的总面积应小于各个外表面可铺设的面积．

因此得到了小屋的透视图如图2所示.

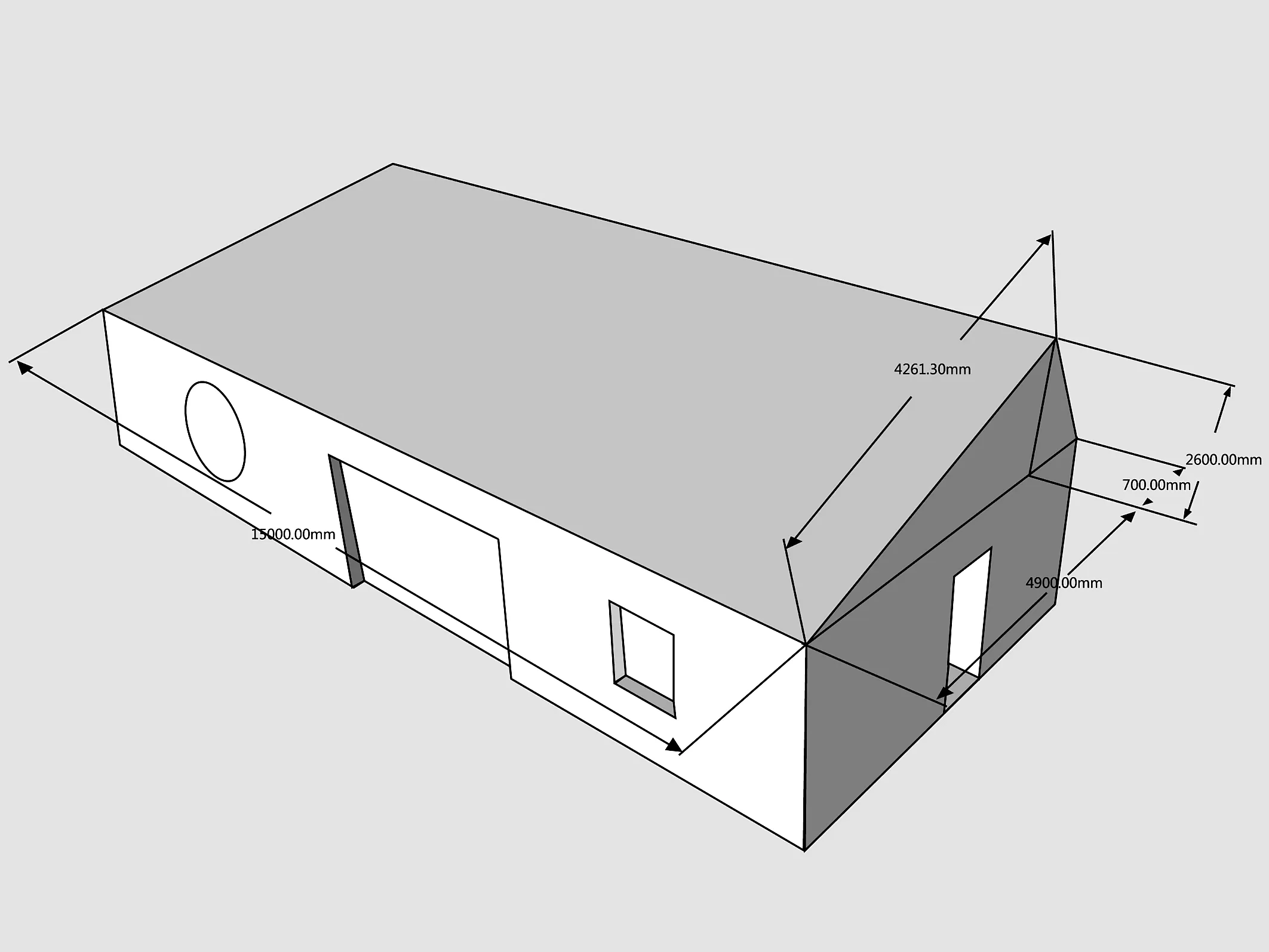
图2 设计小屋的透视图Fig. 2 The perspective drawing of the cabin

由于所设计的太阳能小屋屋顶与水平面的角度为该地区的最佳倾角，因此选择用贴附的方式铺排光伏电池,从而仿照式(1)模型求解方法，对此问题进行求解，得到如下结果.

表6 设计的小屋优化铺排后光伏电池数量及串并联方式

由于倾角相同，可以由问题二屋顶电池的发电计算.根据单个元器件寿命内发电量表可知A3电池寿命内总发电量为12598 kWh，其单价为2980元/个.逆变器SN15的转化效率为94%，逆变器SN7的转化效率为90%.那么单个电池经过逆变器SN15转化后总发电量为11842 kWh，经过逆变器SN7转化后总发电量为 11338 kWh,该列阵发电量为 11842*36+11338*9=528354 kWh，利润为528354*0.5= 264177元.成本为22000+10200+2980*45= 166300元,所以收益为 97877元.根据该收益，可以按照每年(等效于100%效率下31.5年)的收益固定来计算得到回报周期，换算成标准的31.5年的时间t=31.5*97877/264177=11.67年.由于最后10年的效率为80%，之前15年的效率为90%.换算之后的年份为14.0年,即回报周期为21年.

此指标反映出小屋重新设计后不需架空，且回报年限与采用架空设计的屋顶差别不大，这样间接省去了架空的成本，也降低了风险，并且发电总量较采用架空处理的反而更多.

3 结 论

对于给定尺寸的小屋在其外表面合理铺设光伏电池，利用光伏电池将太阳辐射能量转化为电能.采用贴附与架空的形式铺设，以单位面积光伏电池效益的最大化作为目标函数，同时考虑小屋全年太阳能光伏发电总量、单位发电量的费用两个指标，将外表面可铺设面积对光伏电池数量的限制、光伏电池的连接形式、逆变器对光伏电池列阵的要求等作为约束条件，建立目标规划.在基于山西大同市的地理位置与气象条件的数据基础上，计算可以得到光伏电池寿命期内的发电总量、经济效益以及投资的回收年限，得出了架空方式降低了投资回收年限，效果更优的结论.文章的最后给出了满足一定条件的基于以上模型所设计的太阳能小屋.

注：本文为全国大学生数学建模竞赛一等奖获奖论文.

[1] 刘振宇,冯华,杨仁刚.山西不同地区太阳辐射量及最佳倾角分析[J].山西农业大学学报:自然科学版，2011,31(3):272-276.

[2] 徐丰,王波,张海龙.建筑日照分析中太阳位置计算公式的改进研究[J].重庆建筑大学学报,2008,30(5):130-134.

[3] 张鹤飞.与太阳辐射量有关角度的定义和计算公式[J].能源工程，1986,3:31-34.

[4] 韩斐,潘玉良,苏忠贤.固定式太阳能光伏板最佳倾角设计方法研究[J].工程设计学报,2009,16(5):348-353.

TheDesignofSolarHouse

GAO Huayue1, HU Lu2, FENG Shanshan1, HE Yingyu1

(1.College of Science, Hangzhou Normal University, Hangzhou 310036, China; 2.School of Education Science, Hangzhou Normal University, Hangzhou 310036, China)

In view of Datong’s geographical position and meteorological data, this paper used a series of optimization methods to reasonably lay the photovoltaic cells for specified dimensions hut, and discussed the investment and returns. The conclusion was that overhead mode could reduce the investment recovery period. Finally, a solar house which can meet certain requirements was designed which could reduces the cost but obtain more benefits.

goal programming; photovoltaic cells; optimum tilt angle; heuristic algorithm; solar house design

2013-01-17

何颖俞(1973—),女，讲师，博士，主要从事运筹学与控制论方向.E-mail：hyy122773@126.com

10.3969/j.issn.1674-232X.2013.05.008

O29

A

1674-232X(2013)05-0422-07