一类利率为二阶自回归相依结构离散时间风险模型的破产问题

乌峰杰，张慧增

(杭州师范大学理学院，浙江 杭州 310036)

一类利率为二阶自回归相依结构离散时间风险模型的破产问题

乌峰杰，张慧增

(杭州师范大学理学院，浙江 杭州 310036)

研究一类利率为二阶自回归相依结构离散时间风险模型的破产概率.在总资本净损失与利率相对独立的情形下，利用递推方法得到了最终时间破产概率的Lundberg型上界，所得结果部分地推广了古典风险模型及其现有部分结果.

离散风险模型；破产概率；Lundberg上界；二阶自回归

0 引 言

学习了很多经典风险理论之后，发现人们从不同的角度对模型进行了推广，使之更加符合实际风险运作，其中在模型中引入随机利率是风险研究的一个热点问题.文献[1]在离散时间风险模型中引入独立同分布的随机利率得到了Lundberg不等式；文献[2]中引入一阶自回归相依随机利率并考虑保费收取时间对盈余的影响得到了破产概率的上界；文献[3]研究了利率为Markov链时破产概率的上界以及累积净损失Zn服从重尾分布时破产概率的渐近形式；文献[4]针对利率波动较小、利率相关性增强的情况建立了一个具有二阶自回归相依利率结构的离散时间风险模型，只给出了利率为二阶自回归离散时间风险模型破产前盈余大于给定水平x的概率以及破产前最大盈余的分布，利用全概率公式得到了破产概率的积分表达式，且得到了一个更精确的指数型上界，而这个上界是与保险公司的实际运营情况相符的.

以上都在不同的随机利率下研究破产概率的上界或不等式，而针对利率波动较小、相关性增强的情况讨论较少，本文在Cai[2]的风险模型下建立了一个具有二阶自回归相依利率结构的离散时间风险模型，在其相同的条件下采用数学归纳法和更新迭代技巧易得该模型所描述的破产概率的积分表达式及其最终时间破产概率的Lundberg型上界，同时简化了文献[4]中所提到的上界.通过进一步研究可以看到,具有一阶自回归相依利率结构的风险模型将成为本文模型的一种特殊情况，这在一定意义上推广了文献[2,5-6]的相关结论.

1 预备知识

考虑下述离散时间风险模型[2]

Uk=Uk-1(1+Ik)-Zk,k=1,2,…,

(1)

Ik=αIk-1+βIk-2+Wk,k=1,2,…，

(2)

式(1)等价于

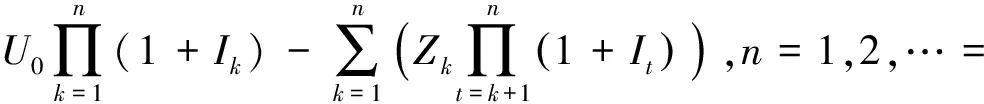
(3)

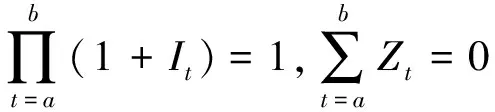
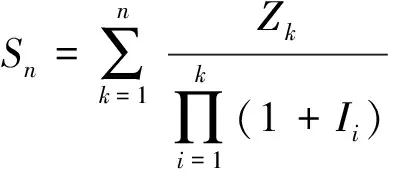
则式(3)等价于

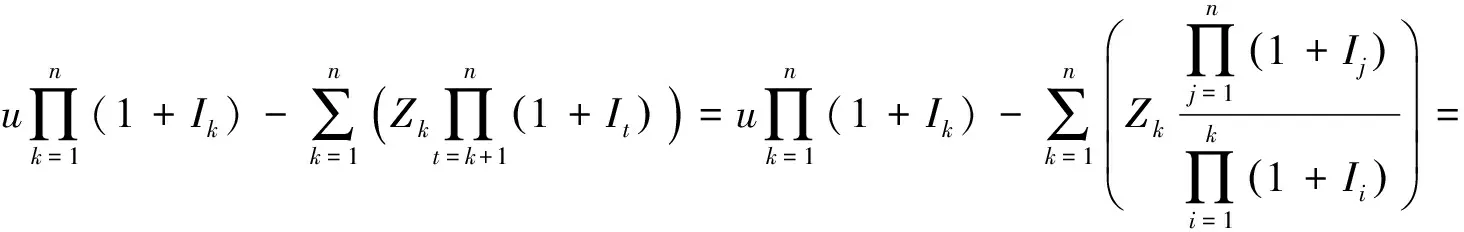
(4)

Ik=αIk-1+Wk,k=1,2,…，

(5)

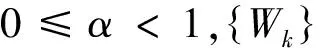
2 破产概率的积分方程

引理1对任意的n=1,2,…,u≥0,ia,ib≥0，有

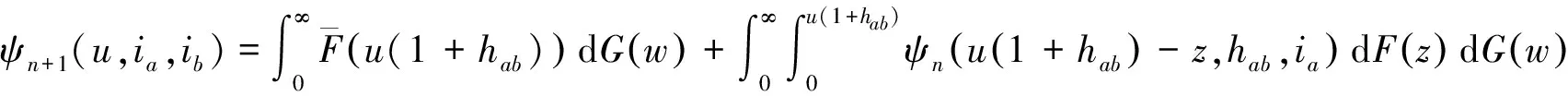
即

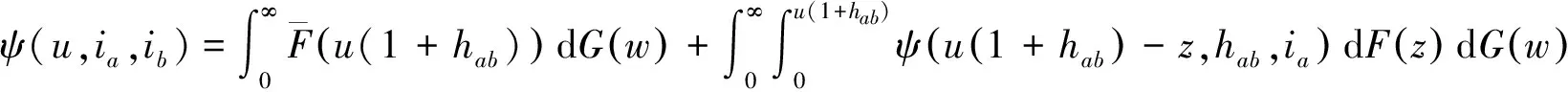
其中hab=I1=αia+βib+w.

证明在事件A0发生的条件下，给定W1=w,Z1=z，记事件由式(1)、(2)易知

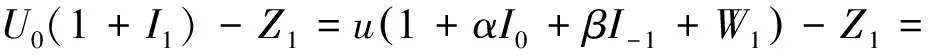
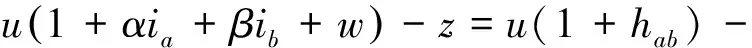
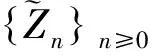
(2)自直线x-y+4=0上任意一点P(x,y)作圆C:x2+y2=4的两条切线，切点分别为A、B，以此为条件，你认为有哪些问题可以研究？请你把问题编写完整，并尝试解答．

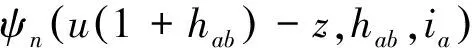
由以上递推可得

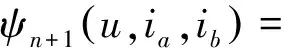
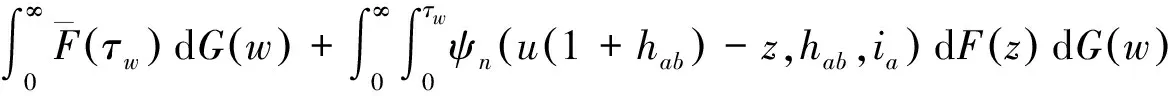
上式两端令n→∞，由Lebesgue控制收敛定理，可得

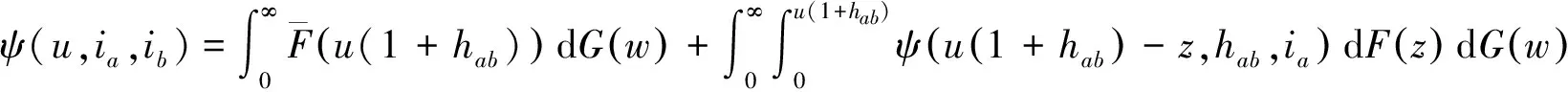
引理1证毕.

3 最终破产概率的相关结论

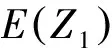
E(eγabZ1|A0)=1，

(6)

则对所有a,b=0,1,2,…，W1≥0有

E(eγ(Z1-u(1+I1))|A0)≤1

(7)

E(eγ(Z1-u(1+I1))W1|A0)≤1,

(8)

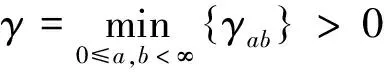
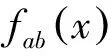
下证式(8)：由于Jessen不等式，可得

E(eγ(Z1-u(1+I1))W1|A0)≤(E(eγ(Z1-u(1+I1))|A0))W1≤1.

综上所述，引理2证毕.

定理1在引理2的条件下，有

ψ(u,ia,ib)≤β1E(eγZ1)E(e-γu(1+αia+βib+W1)|A0)，

(9)

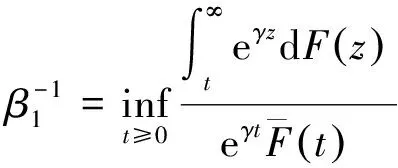
证明对任意的x≥0，有

(10)

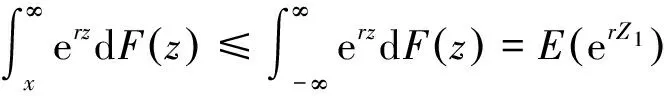
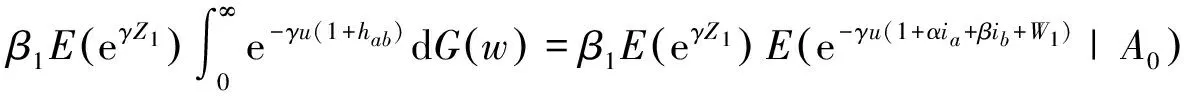
其中hab=I1=αia+βib+w.

假设对任意事件A0发生的情形下，有

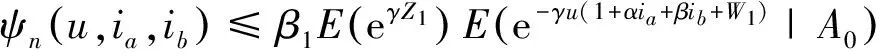
(11)

则对任意0≤z≤τw，由式(7)、(8)、(11)和h=I1≥0可得

(12)

故由引理1，式(10)和(12)得

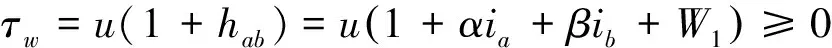
由数学归纳法知，不等式(11)对任意的n=1,2,…,均成立.在式(11)两端对n取极限可得不等式(9).综上所述，定理1证毕.

[1] Cai Jun. Discrete time risk models under rates of interest[J]. Prob Eng Inf Sci,2002,16(3):309-324.

[2] Cai Jun.Ruin probability with dependent rates of interest[J]. Appl Prob,2002,39(2):312-323.

[3] Cai Jun, Dickson D. Ruin probabilities with a Markov chain interest model[J]. Insurance:Mathematics and Economics,2004,35(3):513-525.

[4] 李娜芝.几类带利率的离散风险模型的破产概率[D].长沙：中南大学,2009.

[5] 孔繁超,于莉.具有相依利息率的离散时间保险风险模型的破产问题[J].高等应用数学学报：A辑,2005,20(3):320-326.

[6] 刘东海,刘再明.利率相依的离散时间保险风险模型的破产问题[J].经济数学,2008,25(2):128-131.

[7] Shaked M, Shanthikumar J. Stochastic orders and their applications[M].San Diego: Academic Press,1994.

RuinProbabilityofaDiscrete-timeRiskModelunderInterestRateswithAutoregressiveStructureofOrder2

WU Fengjie, ZHANG Huizeng

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

This paper investigated the ruin probability of a discrete-time risk model under interest rates with autoregressive structure of order 2. The net loss of total capital and interest rates were assumed to be independent, and then the Lundberg upper bound of the final time ruin probability was derived by recursive method, which showed that the established bound extended the classical risk model and partial existing results.

discrete-time risk model; ruin probability; Lundberg upper bound; order 2 autoregressive model

2013-03-29

国家自然科学基金项目(11001070).

张慧增(1976—),男，副教授，博士，主要从事概率论和数理统计研究.E-mail:zhanghz789@163.com

10.3969/j.issn.1674-232X.2013.04.009

O211.6MSC201062P05;91B30

A

1674-232X(2013)04-0327-05