Time Periodic Solution of the Relativistic Boltzmann Equation

2013-10-28YUHongjun

华南师范大学学报（自然科学版） 2013年6期

关键词：霍英东方程解国家自然科学基金

YU Hongjun

(School of Mathematical Sciences, South China Normal University, Guangzhou 510631,China)

TimePeriodicSolutionoftheRelativisticBoltzmannEquation

YU Hongjun*

(School of Mathematical Sciences, South China Normal University, Guangzhou 510631,China)

The existence and stability of the time periodic solution to the relativistic Boltzmann equation around the relativistic Maxwellian in the torus are obtained. The time decay of solution to the linearized relativistic Boltzmann equation is obtained by using compensating function and basic energy estimates. By this and the contraction mapping methods the existence and stablility of time periodic solution to the relativistic Boltzmann equation are shown.

Keywords： relativistic Boltzmann equation; relativistic Maxwellian; time periodic solution; existence; stability

In this paper, we consider time periodic solution of the relativistic Boltzmann equation

(1)

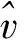
F(u)G(v)]dudω,

(2)

where dωis a surface measure on the unit sphere2, andσis the scattering kernel satisfying some conditions given later. As usual, we abbreviateF(t,x,u) byF(u), etc., and use prime to represent the moment after collision. For the relativistic model, the conservations of momentum and energy are given by

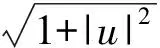
(3)

(4)

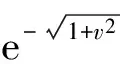
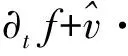
(5)

Lf=μ-1/2{Q(μ,μ1/2f)+Q(μ1/2f,μ)},

and the nonlinear collision operator is

Γ(g1,g2)=μ-1/2Q(μ1/2g1,μ1/2g2).

It is well-known thatLcan be written asLf=ν(v)f+Kfwith the collision frequencyν(v) defined by

(6)

and the operatorKby

μ1/2(u′)f(v′)-μ1/2(v′)f(u′)]dudω.

For the scattering kernelσ(g,θ) as in[2-3], we assume

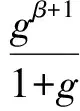
(7)

wherec1andc2are positive constants, 0≤δ<1/2, 0≤β<2-2δ, and eitherγ≥0 or

Under these conditions onσ(g,θ), it was shown in [4] thatKis compact onL2(3). And from [2-3], we know that there is a constantC>1 such that

(8)

By the H-theorem,Lis dissipative and the null space ofLis spanned by the five collision invariants

(9)

LetPbe the projection of the spaceL2(3) to the null spaceinvvariable. We can decomposef(t,x,v) as

f(t,x,v)=Pf+(I-P)f.

(10)

Here,Iis identity,Pfrepresents the macroscopic part and (I-P)fthe microscopic part respectively.

(11)

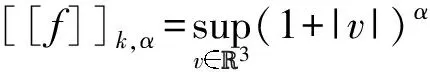
furnished with the same norm. Throughout this paper, we useCto denote a generic positive constant which may vary from line to line.

Time periodic solution of classical Boltzmann equation was first solved by Ukai[5]through the results of spectral analysis[6-7]and contraction mapping methods. It was shown in [8] that the Boltzmann equation with external force admits the time periodic solution by the energy estimates and the results of [6]. On the other hand, the linearized relativistic Boltzmann equation was solved by Dudy1/2ski and Ekiel-Jezewska[4]. Later Glassey and Strauss[2]obtained the global solution of the relativistic Boltzmann equation near a relativistic Maxwellian in the torus, where a more restrictive assumption on the scattering kernel. And then they also obtained the global solution of the relativistic Boltzmann equation near a relativistic Maxwellian in the whole space[3]. The restrictive assumption on the scattering kernel[2]in the torus was removed and the results[2-3]were also obtained[9]by the energy methods. Based on the compensating function[3,10], the new energy methods was devised[11]to obtain both existence and the optimal time decay rate of relativistic Boltzmann and Landau equations without using the results of spectral analysis[6-7]. There are also other studies on the classical or relativistic Boltzmann, see [1,12-14] and the references therein.

Although there are some investigations about the time periodic solution to the classical Boltzmann equation, there is no study about relativistic Boltzmann equation. In this paper, we study the existence and stability of the time periodic solution to the relativistic Boltzmann equation around the relativistic Maxwellian in the torus. We first obtain the time decay of solution to the linearized equation by the compensating function[3,10-11]and by this we use contraction mapping methods to show the existence of time periodic solution to the relativistic Boltzmann equation by the similar methods as[5]. Finally we also show the stability of such a time periodic solution.

1 Existence of the Time Periodic Solution

In this section, we will establish the basic energy estimates in order to obtain the time decay of solution to the linearized relativistic Boltzmann equation and then show the existence of the time periodic solution to (5). For this, we write the linearized equation as

(12)

Lemma1Assumek≥1,α>3/2 andf0satisfies (11). For the solution of the equation (12), we have the following time decay estimate

[[f(t)]]k,α≤ce-c1t[[f0]]k,α.

(13)

ProofBy using compensating function of (12), we can obtain the key estimate as[3,10-11]:

Herek>0 is small enough and(t,ξ,v) is the Fourier transform off(t,x,v) aboutx.

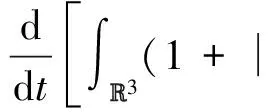
By the properties of the Fourier transform, we have

δ2|||xPf|||k-12≤0.

(14)

By the definition of the projectionP, we can write

Pf=a(t,x)μ1/2+b(t,x)·vμ1/2+c(t,x)|v|2μ1/2.

By the assumption (11), we have

By this and the Poincaré inequality we can obtain

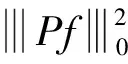
C‖x(a,b,c)‖2≤C.

(15)

On the other hand, we can have from the properties of compensating function[3,11]that

We define

(16)

which implies that

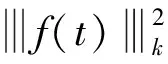
(17)

We rewrite the linearized equation (12) as

(18)

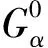
Thus we have from the Duhamel’s formula that

f(t)=e-tBf0=e-tAf0-(e-tAK)*e-tBf0.

Or we have

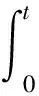
(19)

Recall the properties of the operatorKin [2-3] that for anyα≥0 andk≥0,

K:Gα(Hk)Gα+η(Hk) andL2(Hk)G0(Hk) boundedly,

(20)

whereη>0. Notice from (8) thatν(v)≥cfor some constantc>0. By this and the first relation of (20), we iterate in this manner

[[f(t)]]k,m≤Ce-ct[[f0]]k,m+

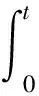
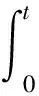
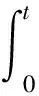
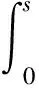
C(1+t)e-ct[[f0]]k,m+

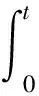
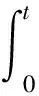
Eventually we have the following: for somec0>0

[[f(t)]]k,m≤Ce-c0t[[f0]]k,m+

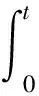
(21)

By using (21) and the second relation of (20), we also obtain

[[f(t)]]k,m≤Ce-c0t[[f0]]k,m+

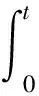
(22)

Notice that for anyα>3/2,|||h|||k≤C[[h]]k,α. By this we combine (17) and (22) to obtain

[[f(t)]]k,α≤ce-c1t[[f0]]k,α.

In the following we will use Lemma 1 to prove the existence of time periodic solution to (5), which is our first main results.

Then there exist positive constantsa0anda1such that whenever supt[[(t)]]k,α≤a0, the problem (5) has a unique solutionfper=fper(t,x,v) which is periodic intwith the same periodTand satisfies (11) and

ProofIn order to obtain the time periodic solution of (5). We will use the arguments developed in [5]. For this we define

(f)(t)=e-(t-s)B{Γ(f(s),f(s))+(s)}ds.

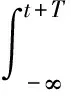
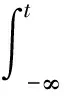
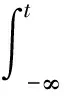
Thus it suffices to find the fixed point ofin a proper complete metric space.

(23)

By the Duhamel’s formula, we obtain

For the termI1(t), we can obtain

For the termI2(t), we can have from (20) that

By the above three estimates, we have

(24)

By (23) and (24) we can iterate the following inequality

(25)

We have from (25) that

(26)

In what follows we shall show that(f) has a unique fixed point(t).

By the above definition ofΦ, we have

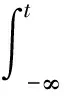
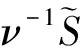
(27)

By Theorem 2.1 in [2], for anyα≥β/2 andk>3/2, one has

C[[h1]]k,α[[h2]]k,α.

(28)

It follows from this and (26) that

(29)

By the assumption, we have

(30)

We define the complete metric space

k>3/2,α>(3+β)/2}.

By (29) and (30) it follows from (27) that

(31)

Noticing thatΓ(h1,h2) is a bilinear operator, we have

Γ(f1,f1)-Γ(f2,f2)=

Γ(f1+f2,f1-f2)+Γ(f1-f2,f1+f2).

By this and (28), we have

[[ν-1Γ(f1+f2,f1-f2)]]k,α+

[[ν-1Γ(f1-f2,f1+f2)]]k,α≤

C[[f1+f2]]k,α[[f1-f2]]k,α.

This implies that

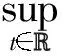
By (27) and the above estimates, we have

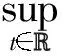
(32)

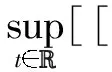
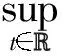
2 Stability of the Time Periodic Solution

In the preceding section we show the existence of the time periodic solution to (5) with time periodic source term. In this section we shall prove the stability of such a time periodic solution. For this, for any fixed timet0, we consider the problem

(33)

Settingg(t)=f(t)-fper(t), the problem (33) takes the form

(34)

withg(t0,x,v)=f0(x,v)-fper(t0). HereLperg=Γ(fper,g)+Γ(g,fper).

Our main results in this section are as follows.

Theorem2Letk>3/2 andα>(3+β)/2. Assume that (7) on the scattering kernelσ(g,θ). Letfper(t) be the time periodic solution constructed in Theorem 1. Then there exist positive constantsδ0andδ1such that whenever initial dataf0satisfies

[[f0(x,v)-fper(t0)]]k,α≤δ0,

the problem (33) has a unique global solutionf=f(t,x,v) satisfies

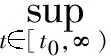
δ1[[f0(x,v)-fper(t0)]]k,α.

(35)

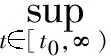
δ1e-ct[[f0(x,v)-fper(t0)]]k,α.

(36)

ProofBy the preceding section, we shall show

Γ(g(s),g(s))}ds

(37)

has a unique fixed point in the following space

We define

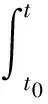
By Lemma 1 we have for any fixed timet0≤0,

which implies that

By the Duhamel’s formula, we obtain

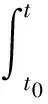
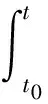
For the termJ1(t), we can obtain

For the termJ2(t), we can obtain

By the above three estimates, we have

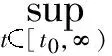
Finally we can iterate the following inequality

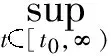
(38)

We can rewrite (37) as follow:

N[g](t)=e-(t-t0)Bg0+Φ[ν-1Lperg]+

Φ[ν-1Γ(g,g)].

(39)

It follows from Lemma 1 that

ClearlyPΓ(f,g)=0. By (28) and (38) we can obtain

and

Finally we have

Notice that

N[g1](t)-N[g2](t)=Φ[ν-1Lper(g1-g2)]+

Φ[ν-1(Γ(g1,g1)-Γ(g2,g2))].

(40)

By the similar arguments we can obtain

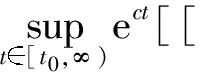
Choosingδ0anda0small enough, we know that[g] is a contraction mapping and has a unique fixed pointg(t), which is our desired solution. Thus (36) is shown and (35) can be shown by a similar methods. This completes the proof of Theorem 2.

[1] CERCIGNANI C,KREMER M G. The relativistic Boltzmann equation: Theory and applications[M]. Switzerland:Birkhauser Verlag, 2002.

[2] GLASSEY R T,STRAUSS W A. Asymptotic stability of the relativistic Maxwellian[J]. Publ Res Inst Math Sci,1993,29:301-347.

[3] GLASSEY R T, STRAUSS W A.Asymptotic stability of the relativistic Maxwellian via fourteen moments[J].Transport Theor Stat,1995,24:657-678.

[4] DUDY1/4SKI M,EKIEL-JEZEWSKA M. On the linearized relativistic Boltzmann equation[J]. Comm Math Phys, 1988,115:607-629.

[5] UKAI S. Time period solutions of the Boltzmann equation[J].Discrite Continuous Dynamical Sys:Ser A,2006,14:579-596.

[6] UKAI S. On the existence of global solutions of mixed problem for non-linear Boltzmann equation[J]. Proc Japan Acad,1974,50:179-184.

[7] UKAI S, YANG T. Mathematical theory of Boltzmann equation[M/OL]. Lecture Notes Series-No 8, Hongkong: Liu Bie Ju Center of Mathematical Sciences, City University of Hongkong, 2006.http:∥www6.cityu.edu.hk/rcms/publications.htm.

[8] DUAN R J, UKAI S, YANG T,et al. Optimal decay estimates on the linearized Boltzmann equation with time dependent force and their applications[J].Comm Math Phys,2008,277:189-236.

[9] HSIAO L,YU H J. Asyptotic stability of the relativistic Maxwellian[J]. Math Meth Appl Sci,2006,29:1481-1499.

[10] KAWASHIMA S.The Boltzmann equation and thirteen moments[J].Japan J Appl Math,1990,7:301-320.

[11] YANG T,YU H J. Hypocoercivity of the relativistic Boltzmann and Landau equations in the whole space[J]. J Differ Equations, 2010,248(3):1518-1560.

[12] DUDY1/4SKI M,EKIEL-JEZEWSKA M. Global existence proof for relativistic Boltzmann equation[J]. J Stat Phys,1992,66:991-1001.

[13] GLASSEY R. The Cauchy problem in kinetic theory[M].Philadelphia, PA: SIAM, 1996.

[14] STRAIN R M. Asyptotic stability of the relativistic the Boltzmann equation with soft potentials[J]. Comm Math Phys,2010,300:529-597.

2013-06-20

国家自然科学基金项目(11071085);霍英东教育基金会高等院校青年教师基金项目(121002)

1000-5463(2013)06-0019-07

O175.29

10.6054/j.jscnun.2013.09.003

相对论Boltzmann方程的时间周期解

喻洪俊*

(华南师范大学数学科学学院，广东广州 510631)

得到了周期区域上靠近稳态的相对论Boltzmann方程的时间周期解的存在性和稳定性．通过利用补偿函数和基本的能量估计，得到了线性化的相对论Boltzmann方程解的时间衰减，根据此结果和压缩映像原理，证明了相对论Boltzmann方程的时间周期解的存在性和稳定性．