基于宽松下近似概念的连续型决策表的属性约简方法

张群峰，张天一

(1.河北大学 数学与计算机学院，河北 保定 071002；2.河北大学 临床医学院，河北 保定 071000)

基于宽松下近似概念的连续型决策表的属性约简方法

张群峰1，张天一2

(1.河北大学 数学与计算机学院，河北 保定 071002；2.河北大学 临床医学院，河北 保定 071000)

针对连续型决策表，利用模糊相容关系对样例聚类产生模糊决策表,运用宽松下近似概念定义属性重要度,利用函数弹性概念定义决策属性关于条件属性的敏感度，将其作为属性重要度的权重得到加权重要度，并以此为启发式信息提出了一种连续型决策表的属性约简方法.

决策表；属性约简；模糊粗糙集

决策表是一种广泛存在的信息系统，如何对其条件属性进行约简是机器学习领域的一个热点问题.表1是一个小型决策表的例子.

表1中，U={1,2,3,4,5,6}为论域，C={A1,A2,A3,A4,A5}为条件属性集，D为决策属性.因为属性值可以是连续的实数，所以此决策表称为连续型决策表.

连续型决策表的一般形式为四元组(U,C,D,f)，其中U={i|i=1,2,…,m}为论域，i=1,2,…,m为样例的代号;C={Aj|j=1,2,…,n}为条件属性集合；D为决策属性；f:U×(C∪D)→R,f(i,Aj)=Aj(i)=aij,f(i,D)=di,i=1,2,…,m,j=1,2,…,n为信息函数，其中R为实数集合.

所谓对连续型决策表进行属性约简，是指寻找条件属性集的一个子集，并使其具有与整个条件属性集合相同的分类能力[1].在模糊粗糙集理论中，条件属性子集的分类能力可以用决策属性对其依赖度表示，而依赖度指决策属性相对该条件属性子集的正域在论域中所占的比例.

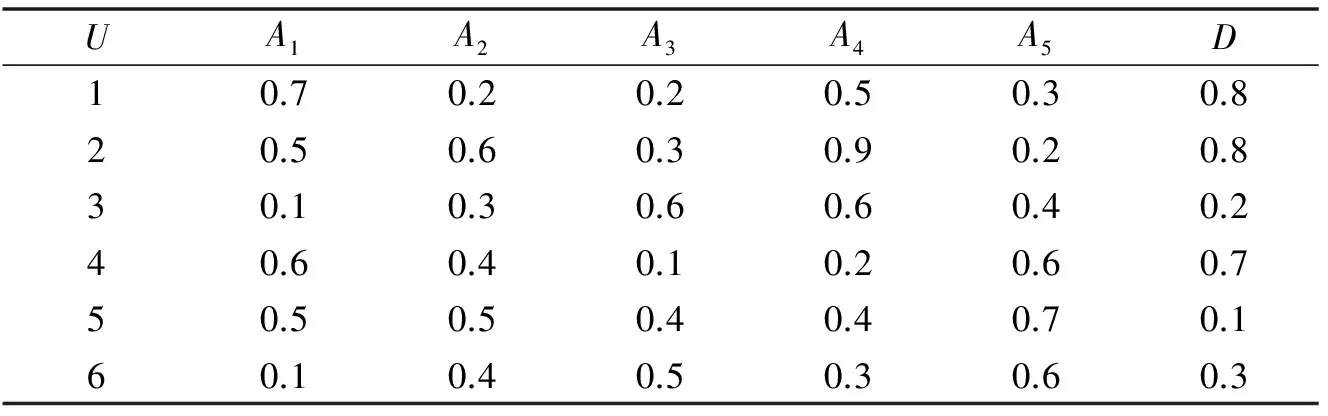
表1 决策表的例

利用粗糙集理论计算决策表属性约简的通常做法是，先找出对保持整个条件属性集合分类能力必不可少的条件属性组成属性的核.若核具有与整个条件属性集相同的分类能力，则核就是所求的属性约简；否则，将核作为候选约简，然后依据某种启发式信息选择核外属性不断加入候选约简，直到候选约简具有与整个条件属性集相同的分类能力.因此设计高效约简算法的关键是如何构建这种启发式信息.

常见的构建启发式信息的方法有2种.一种通过辨识矩阵[2]，另一种通过度量条件属性对某属性子集的分类能力的影响.第2种方法就是要计算去除或添加一个条件属性所导致的决策属性对该属性子集依赖度的变化.由于依赖度概念由正域描述，而正域是决策类的下近似的并集，所以选用恰当的下近似概念是第2种方法的关键问题.

对这个问题，相关的文献采取了不同的解决方法.文献[3]采用了文献[4]提出的下近似概念，这种下近似概念是单个条件属性的模糊划分对决策类的近似表示.但是，为了计算属性约简，必须从单个条件属性推广到条件属性子集的情形，这就需要计算属性的模糊划分的笛卡尔乘积[5]，从而引起计算量的指数式增加.在计算机科学中这种算法通常被认为是不可取的.文献[5]引用文献[6]提出的基于模糊t-模和模糊蕴含算子的下近似概念，避开了模糊划分概念，从而降低了计算的复杂性.

但是，如文献[7]指出的那样，文献[5]利用的是通常意义下的下近似概念，其外延较小，作为决策概念的子集，没有达到对模糊决策概念的最大逼近.同时，该方法所用下近似概念要求计算模糊相容关系的传递闭包，有时计算量较大.另外，该方法在产生模糊决策表时运用了独立于模糊粗糙集理论的模糊化方法产生模糊决策表，而没有充分利用模糊粗糙集理论中模糊相容关系的信息.

文献[3，5]均未考虑决策属性对条件属性的敏感性.敏感性的概念在机器学习的其他领域已得到充分重视，例如在神经网络中将敏感性作为训练过程中的重要启发式信息.

基于以上分析，本文针对连续型决策表，首先根据模糊相容关系对样例进行聚类产生模糊决策表.其次，由于模糊粗糙集理论中的宽松下近似概念是建立在模糊相容关系基础上，且比文献[5]所用的下近似概念能更加准确地逼近决策类，故本文引用宽松下近似概念来定义条件属性的重要度.最后，本文引入新的属性敏感度定义，将其作为条件属性重要度的权重从而得到加权重要度，并以此作为启发式信息对连续型决策表进行属性约简.

1 预备知识

1.1模糊粗糙集的宽松下近似概念

设X为给定的论域，R为X上的模糊相容关系，即R满足自反性R(i,i)=1,∀i∈U和对称性R(i,j)=R(j,i),∀i,j∈U.用F(X)表示X上的全体模糊集合，则对于任意A∈F(X)，A的宽松下近似定义为[7]

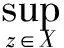
(1)

而通常的下近似定义为

(2)

其中T为模糊t-模而I为模糊蕴含算子.

一般地有R↓A⊆R↑↓A⊆A，下例说明第1个集合可能是第2个集合的真子集[7],即包含关系中的等号可能不成立.

例 设X=[0,1]，A∈F(X)定义为A(x)=x，∀x∈X,X上的模糊相容关系定义为

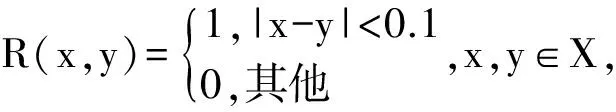
则对任何t-T和任意模糊蕴含算子I有(R↓A)(0.95)=0.85，(R↑↓A)(0.95)=0.9，即(R↓A)(y)⊂(R↑↓A)(y).

1.2函数的弹性概念

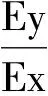
在离散情形，若y=f(x)满足yi=f(xi)，i=1,2,…,n,本文将弹性概念变形为差商形式

(3)

2 构建模糊决策表

利用模糊粗糙集理论进行属性约简，首先要把连续型决策表转换成模糊决策表.通常的模糊化方法事先人为指定模糊集的个数和形式，这样难免带有一定的主观性.本文考虑到，2个样例若有很高的相似性，则应对同一个模糊集的隶属度应相近；否则，应尽量归于不同的模糊集.而模糊相容关系反映了样例的相似程度，因此采取基于模糊相容关系的聚类方法产生模糊集.刻划样例之间的相似程度的模糊相容关系已得到详细研究[8]，本文以如下模糊相容关系[5]为例进行描述：

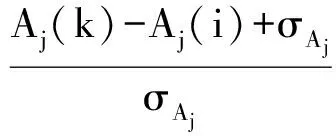
(4)

其中σAj为属性Aj的属性值的均方差.

选定模糊相容关系后，本文结合参考文献[8]中所述聚类方法，提出如下产生模糊决策表的算法：

算法1 构建模糊决策表

输入：连续型决策表

输出：模糊决策表

步骤1： 对每个属性，计算其相似矩阵；

步骤2：依据相似矩阵的截集矩阵对样例聚类；

步骤3： 对每个类计算其元素的平均相似度，将平均相似度最高的元素i作为聚类中心，并以Aj(i,k),k=1,2,…,n作为属性Aj的一个模糊集.

例如，运用上述算法对表1中条件属性A3和决策属性D分别模糊化的结果如表2和表3所示.

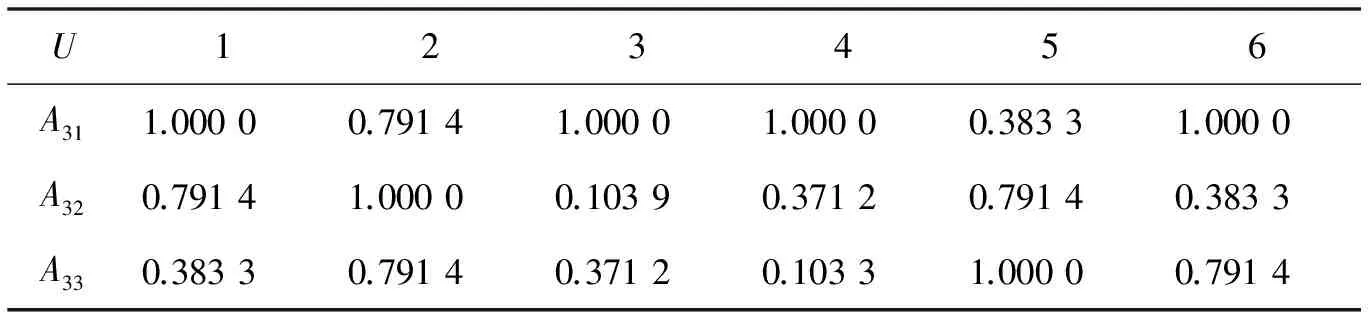
表2 条件属性的模糊化

表3 模糊决策属性的模糊化

3 利用模糊粗糙集理论进行属性约简

3.1决策属性对条件属性子集的依赖度

论域U={i|i=1,2,…,m}上模糊集合的全体记为F(U).根据定义式(1)，任意模糊集合X∈F(U)的RA-宽松下近似为

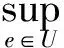
(5)

T(x,y)=min{x,y},

(6)

取I为Lukasiewiz模糊蕴含算子

I(x,y)=min{1-x+y,1},

(7)

进而定义决策属性D相对于条件属性子集A的正域为

(8)

最后，定义决策属性D相对于条件属性子集A的依赖度为

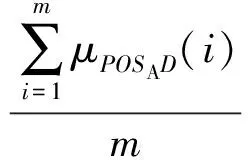
(9)

3.2条件属性的内、外重要度

设A⊆C为条件属性子集，A∈A，则A相对于A的内部重要度定义为

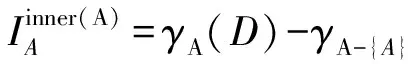
(10)

设A⊆C为条件属性子集，A∈C-A，则A相对于A的外部重要度定义为

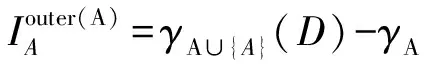
(11)

3.3决策属性相对于条件属性的敏感度

若一个条件属性的值的微小改变能引起决策属性值的剧烈改变，则决策属性对该条件属性变化的反应较灵敏；反之，较迟钝.笔者认为，反应的灵敏或迟钝是决策效率高低的表现，依赖度是决策的确定性程度的度量，依赖度具有本质的意义，而灵敏度和依赖度是相辅相成的关系.因此，灵敏度可以作为属性重要度的权重来构造启发式信息.

将连续型决策表的条件属性看作自变量而将决策属性看作因变量，则决策属性对条件属性的灵敏性可以用离散情形的弹性公式(3)来计算.值得注意的是，这里没有像通常的神经网络敏感性分析中那样用导数作为敏感性的度量.这是因为函数的弹性反应的是函数值对自变量的相对变化量，而导数反映的是函数值对自变量的绝对变化量，而且，弹性没有量纲，更便于比较决策属性关于不同条件属性的敏感性的大小.

运用式(4)可得表1中决策属性关于各个条件属性的弹性如表4所示.

表4 条件属性的弹性

3.4模糊粗糙约简

首先，把整个条件属性集中具有大于零的内部重要度的条件属性称为核属性.所有核属性的集合称为核，记作

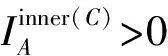
(12)

其次，把能保持整个条件属性集合的分类能力不变的条件属性子集作为条件属性集的模糊约简.

计算属性约简的流程如下：先计算各个条件属性在整个条件属性集合的内部重要度，进而求出条件属性的核.若核不是约简，则将其作为候选约简，并加入相对于候选约简具有最大加权外部重要度的非核属性形成新的候选约简，直到候选约简具有与整个条件属性集有相同的分类能力为止.算法描述如下：

算法2 计算连续型决策表的属性约简

输入：模糊决策表

输出：条件属性集的模糊约简

步骤3：计算γRDT(D).若γRDT(D)=γC(D)，则转第5步；

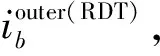
步骤5：输出RDT，结束.

对前述决策表，经计算可得CORE={A5}和属性约简RDT={A1,A5}.

4 结论

本文针对连续型决策表的属性约简问题，提出了一种基于模糊粗糙集理论中宽松下近似概念的解决方法.相对于已有的方法，本文的方法立足模糊粗糙集理论，采用了更准确的宽松下近似概念来逼近决策概念，并结合属性敏感度构造启发式信息计算约简，下一步将考虑在约简的基础上构建模糊决策树.

[1]TSANG E C C, CHEN D G, YEUNG D S, et al. Attributes reduction using fuzzy rough sets[J]. IEEE Trans Fuzzy Syst, 2008, 16(5): 1130-1141.

[2]HE Qiang, WU Congxin, CHEN Degang, et al. Fuzzy rough set based attribute reduction for information systems with fuzzy decisions[J]. Knowledge-Based Systems, 2011(24):689-696.

[3]BHATT R B, GOPAL M. FRCT: fuzzy-rough classification trees[J]. Pattern Anal Applic, 2008, 11(1): 73-88.

[4]DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. Int J Gen Syst, 1990(17 ): 191-208.

[5]JENSEN R, SHEN Q. New approaches to fuzzy-rough feature selection[J]. IEEE Transaction on Systems, 2009,17(4):824-838.

[6]RADZIKOWSKA A M, KERRE E E. A comparative study of fuzzy rough sets[J]. Fuzzy Sets System, 2002,126(2):137-155.

[7]CORNELIS C, COCK M D, RADZIKOWSKA A M. Fuzzy rough sets: from theory into practice [EB/OL].(2008-07-16)[2012-07-10] www.cwi.ugent.be.

[8]高新波. 模糊聚类分析及其应用[M]. 西安：西安电子科技大学出版社，2004.

Reducingtheattributesofdecisiontableswithrealvaluesbasedonlooselowerapproximation

ZHANGQunfeng1,ZHANGTianyi2

(1.College of Mathematics and Computer Science, Hebei University, Baoding 071002, China;

2.College of Clinical Medicine, Hebei University, Baoding 071000, China)

To reduce the attributes of decision tables with real attribute values, a method based on loose lower approximation in fuzzy rough set theory is proposed. First, a fuzzy decision table is generated by using the fuzzy tolerance relation. Second, based on loose lower approximation, the inner importance degree and outer importance degree of condition attributes are defined. By utilizing a combination of importance degree and sensitivity of decision attributes, an algorithm for reducing the decision table is designed and an example is demonstrated.

decision table; attribute reduction; fuzzy rough sets

10.3969/j.issn.1000-1565.2013.04.001

2013-01-17

河北省教育厅科学研究计划资助项目(2009312)；河北省科技厅软科学项目(12457662)；河北省自然科学基金资助项目(F2011201063)

张群峰(1963-)，男，河北成安人，河北大学副教授，主要从事粗糙集理论及应用、机器学习理论方向研究.

E-mail:zhangqunfeng@hbu.cn

O235

A

1000-1565(2013)04-0337-05

MSC201068T05

(责任编辑王兰英)