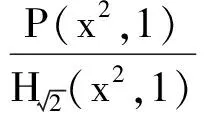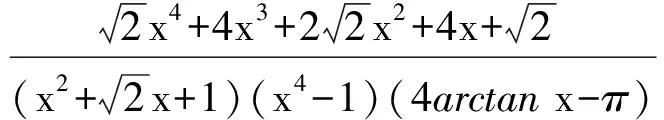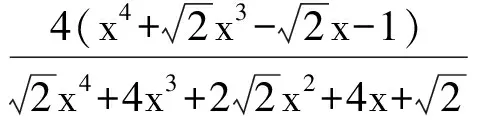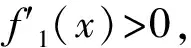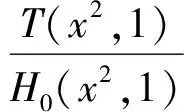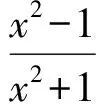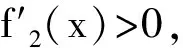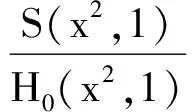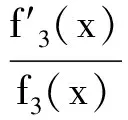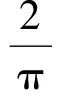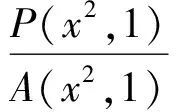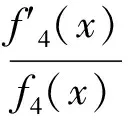一些新的双边不等式
2013-10-28高红亚牛文娟吴迎雪
高红亚,牛文娟,吴迎雪
(河北大学 数学与计算机学院,河北 保定 071002)
一些新的双边不等式
高红亚,牛文娟,吴迎雪
(河北大学 数学与计算机学院,河北 保定 071002)
不等式出现于数学的各个分支,并广泛应用于数学、物理学、力学和工程技术领域.给出了双边不等式成立的一个充分条件,并得到了几个与Seiffert平均、广义海伦平均、算术平均和加权几何平均有关的新的双边不等式.
双边不等式;Seiffert平均;广义海伦平均;算术平均;加权几何平均
区间I上2个正数a,b的平均定义为函数M:I2→I,满足
min{a,b}≤M(a,b)≤max{a,b},∀a,b∈I.
(1)
由上式得
M(a,b)=a,∀a∈I.
M(a,b)称为对称的,若
M(a,b)=M(b,a),∀a,b∈I,∀c>0.
(2)
近年来,解析不等式的研究吸引了诸多数学工作者的兴趣,见文献[1]及其参考文献.双边不等式的一些结果见文献[2-3].
本文首先给出1个双边不等式成立的充分条件,然后给出几个新的双边不等式.
Seiffert[4-5]引入了第1类和第2类Seiffert平均
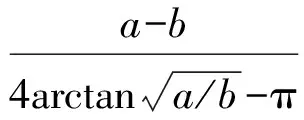
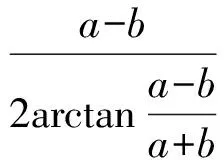
下面的广义海伦平均由Janous[6]引入
算术平均加权几何平均分别定义为
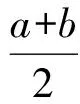
S(a,b)=aa/(a+b)bb/(a+b).
与Seiffert平均和广义海伦平均有关的结果见文献[7-9].与算术平均和加权几何平均有关的结果见文献[3].经典平均的应用见文献[10].
首先证明下面的定理.
定理1 设A(a,b)和B(a,b)为2个对称齐次平均,c为一常数.若函数
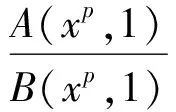
严格单调,且满足

则当f(x)严格递减时,对所有a,b>0,a≠b,双边不等式
cB(a,b) (3) 成立.当f(x)严格递增时,对所有a,b>0,a≠b,双边不等式 B(a,b) (4) 成立.式(3)和式(4)中的常数1和c是最优的. 证明不失一般性,设a>b>0.取xp=a/b>1.因为A(a,b)和B(a,b)为2个对称齐次平均,由式(1)可得 于是 若f(x)严格递减,则对所有x>1,c 下面给出几个双边不等式.因为a,b>0任意,且每个平均都是对称的,所以不妨设a>b>0. 推论1 对任意a,b>0,a≠b,有 (5) 证明令x2=a/b>1,对 取对数再取导数,得 (6) 其中 计算得 得到. 推论2 对任意a,b>0,a≠b,有 (7) 其中常数1和4/π是最优的. 证明令x2=a/b>1,对 取对数再取导数,得 (8) 其中 计算得 得到. 推论3 对任意a,b>0,a≠b,有 H0(a,b) 其中常数1和2是最优的. 证明令x2=a/b>1,对 取对数再取导数,得 因此f3(x)对于任意x>1是严格递增的,推论3的结果由定理1和 得到. 推论4 对任意a,b>0,a≠b,有 (9) 其中常数2/π和1是最优的. 证明令x2=a/b>1,对 取对数再取导数,得 (10) 其中 计算得 得到. [1]张小明,褚玉明.解析不等式新论[M].哈尔滨:哈尔滨工业大学出版社,2009. ZHANGXiaoming,CHUYuming.Newdiscussiontoanalyticinequalities[M].Harbin:HarbinInstituteofTechnologyPress, 2009. [2]NEUANE,SANDORJ.Companioninequalitiesforcertainbivariatemeans[J].AppoAnalDiscreteMath, 2009, 3(1):46-51. [3]DUHongxia.Someinequalitiesforbivariatemeans[J].CommunKoreanMathSoc, 2009, 24(4):553-559. [4]SEIFFERTHJ.Problem887[J].NieuwArchiefvoorWiskunde, 1993, 11(2):176-176. [5]SEIFFERTHJ.Aufgabeβ16[J].DieWurzel, 1995, 29:221-222. [6]JANOUSW.AnoteongeneralizedHeronianmean[J].MathIneqAppl, 2001, 3:369-375. [7]GAOHongya,GUOJianling,YUWanguo.SharpboundsforpowermeanintermsofgeneralizedHeronianmean[J].AbstractandAppliedAnalysis, 2011, 2011:1-9. [8]GAOHongya,GUOJianling.AninequalitybetweenthearithmeticandthesecondSeiffertmeans[J].ArtacticaJournalofMathematics, 2012, 9(1):19-22. [9]GAOHongya,QINYanli.TheoptimalconvexcombinationboundsofcontraharmonicandarithmeticmeansforthesecondSeiffertmean[J].AntarcticaJournalofMathematics, 2012, 9(7):575-580. [10]高红亚,乔金静.微分形式障碍问题解的正规性[J].河北大学学报:自然科学版,2011,31(5):1-5. GAOHongya,QIAOJinjing.Reguearityforsolutionstoobstacteprobtemsfordifferentialforms[J].JournalofHebeiUniversity:NaturalScienceEdition, 2011,31(5):1-5. Somenewcompanioninequalities GAOHongya,NIUWenjuan,WUYingxue (College of Mathematics and Computer Science, Hebei University, Baoding 071002, China) Inequalities appear in all branches of mathematics, and applied in the fields of mathematics, physics, mechanics and engineering.In this paper, a sufficient condition ensuring companion inequalities is given and some new companion inequalities related to Seiffert, generalized Heronian, arithmetic and weighted geometric means are obtained. companion inequality; Seiffert mean;generalized Heronian mean; arithmetic mean; weighted geometric mean 10.3969/j.issn.1000-1565.2013.01.001 2012-04-07 国家自然科学基金资助项目(10971224);河北省自然科学基金资助项目(A2011201011) 高红亚(1969-),男,河北顺平人,河北大学教授,博士,主要从事几何函数论与非线性分析方向研究. E-mail:hongya-gao@sohu.com O178 A 1000-1565(2013)01-0001-04 MSC2010: 26D20 (责任编辑王兰英)