基于大型体育赛事最低门票价格的差别定价研究

高山桂，张 波，宁玉龙

1 问题的提出

20世纪40年代，体育产业作为经济发展的一个重要组成部分在欧洲、北美洲发达资本主义国家兴起。随着经济日新月异的发展，体育赛事规模的逐步扩大和资金需求的日益增长，体育产业表现出快速化、国际化的发展趋势。目前，体育产业和其他产业一样，已经成为国家新的经济增长点。在推动产业结构的调整和升级、扩大就业渠道、增加就业岗位等方面发挥着重要的作用。改革开放以来，我国体育事业以社会化和产业化为方向，拉开了管理体制改革与运行机制转化的序幕。体育赛事领域内的经营活动正在逐渐发展，而门票市场作为体育赛事经营运作的重要组成部分，反映了社会群体对赛事服务产品的认识和关注程度以及门票收入在体育赛事中所占的重要比重。合理的赛事门票价格，不仅可以让举办方获得一定的收益，还可以让更多的体育爱好者参与并享受体育的快乐[1]。

大型体育赛事票价的决策者可以通过不同的定价和售票方式来提高门票的销售量，进而增加利润。为实现利润最大化，门票价格的制定不能太低。过低的价格会使消费者认为赛事质量有问题，从而影响上座率;价格过高，会超过一般居民的支付能力，影响门票的售出量。有时举办方为获得较高的收益对票价实行差别定价。差别定价是指企业以两种或两种以上不同反映成本费用的比例差异的价格来销售一种产品或服务，即价格的不同并不是基于成本的不同，而是企业为满足不同消费层次的要求而构建的价格结构[2]。

影响定价的价格差别理论在体育赛事中发挥着重要的作用，是众多赛事研究者的研究方向。如史兵的《综合型运动会门票定价理论研究》[3]和韩开成的《价格歧视策略在奥运会门票定价中的运用》[4]等论文都从差别价格理论的角度对体育赛事门票的制定提出了可行、合理的方案。在已有研究成果的基础上，本文拟首先估计在使成本得到收回的前提下，最低的平均票价定位是多少，然后在此基础上，运用差别定价理论，实现可观的收益。

本文拟以总投资，主场容量，GDP，赞助费为影响因素，建立其与价格的多元线性回归模型，考查最低的平均门票价格应该定在什么样的水平。如果举办方考虑获取更大利润，可以在最低价的基础上适当提高价格，实现利润的获得。

2 最低平均门票定价模型的建立与求解

2.1 数据的收集与整理

从相关资料中[5]，我们收集到1972年至2008年10届奥运会有关举办地区的平均票价(y)，人均GDP(x1)、总投资(x2)、奥运会主场容量(x3)、赞助费(x4)的数据(见表1)。

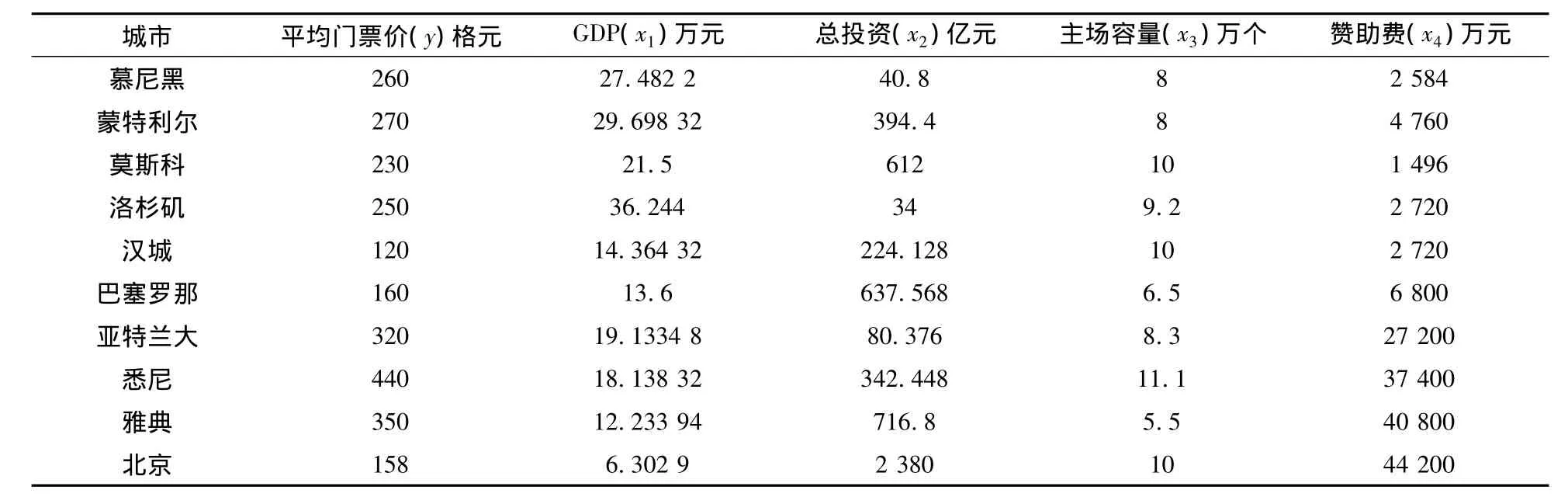
表1 1972～2008年奥运会数据统计

在本问题中，不同变量的测量单位不是完全一样的，为了消除变量的量纲效应，使每个变量都有同等的表现力，要对数据同时进行中心化和压缩化处理[6](具体数据见表 2)，即

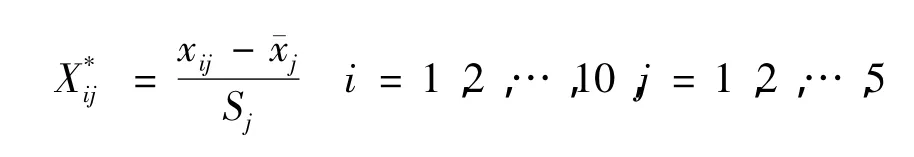
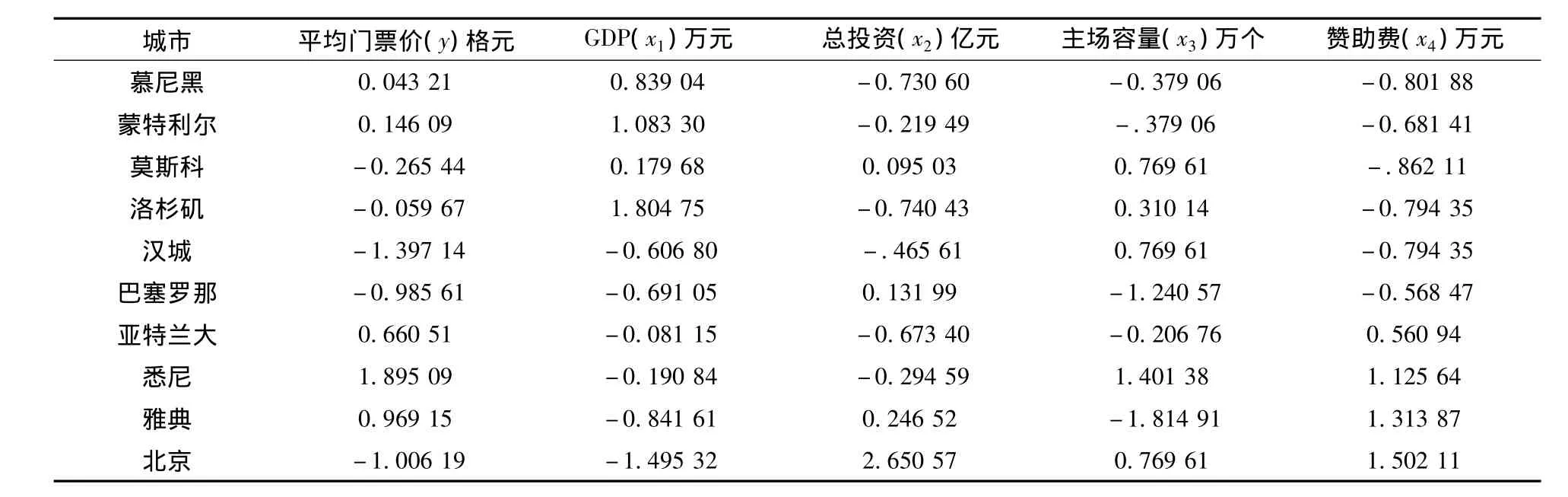
表2 消除量纲后的历届奥运数据

2.2 模型的建立

根据以往的经验为参考，我们假设被解释变量最低平均门票价格与解释变量GDP、总投资、主场容量、赞助费呈线性关系。用Eviews软件用最小二乘估计(OLSE)法建立多元线性回归模型。

假设回归模型为:

y=β0+β1x1+β2x2+β3x3+β4x4+ε

β0、β1、β2、β3、β4是模型中的未知参数，分别称为回归常数和偏回归系数。ε是随机误差项，假设满足两个前提条件:

E(ε)=0 var(ε)= σ2

于是有

E(y)= β0+β1x1+β2x2+β3x3+β4x4

得到多元线性回归方程[6]。

普通最小二乘估计的出发点是使每个样本点(xij，yj)与回归线上的对应点(xij，E(yi))在垂直方向上的偏差距离的总和最小。在多元线性回归方程中，最小二乘估计是寻找参数 β0、β1、β2、β3、β4的估计值0、1、2、3、4，实现最小。

2.3 模型的估计与检验

2.3.1 模型的初步求解 用标准化后的数据建立模型，用Eviews软件进行回归分析，具体结果见表3。

2.3.2 模型的检验

(A)统计检验

(1)拟合优度检验。因为该问题有多个解释变量，所以应参考调整的判定系数¯R2，由表知¯R2=0.962 365，较接近1，因此可以认为拟合优度较高。被解释变量平均门票价格的变化其中96.24%可以被解释变量GDP、总投资、主场容量、赞助费解释。

(2)方程的显著性检验。从表中3可以看出，F统计量对应的概率P值为0.007 105，小于显著性水平α=0.05。所以拒绝方程线性关系不显著的原假设，认为各回归系数不同时为零，被解释变量与解释变量全体的线性关系是显著的，可建立线性模型。

(3)变量的显著性检验。通过上表3可以看出，四个解释变量和常数项都通过了检验，对应的概率P值都小于0.05。所以拒绝变量系数为零的原假设，即变量系数显著不为零，各解释变量对被解释变量的影响是显著的。

表3 Eviews运行结果

(B)计量经济学检验

(1)序列相关性检验。从表3中可以看出DW=2.041 340。当DW在2附近时表明残差序列无自相关，在本例中，DW的值很接近2。所以我们可以认为残差序列无自相关。

(2)解释变量的多重共线性检验。由表4我们可以知道，变量之间的容忍度都比较接近1，表明解释变量之间的多重共线性很弱。

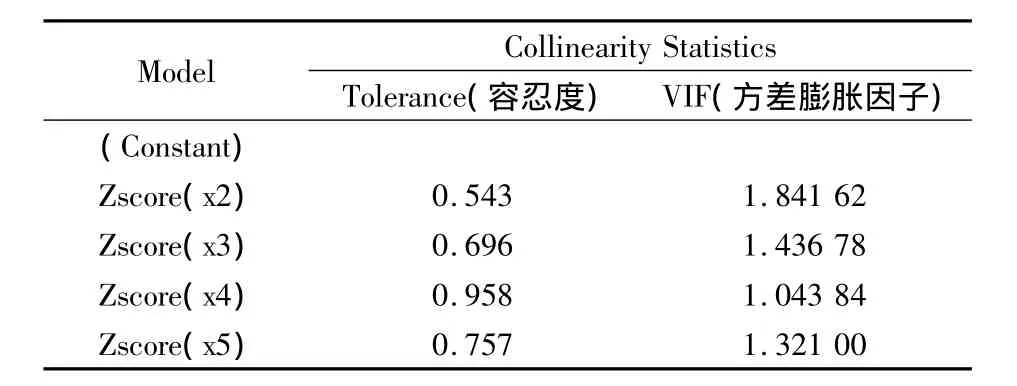
表4 多重共线性检

(3)随机干扰项序列的异方差性检验。从图1中可以看出，随着标准化预测值的变化，残差点在0线周围没有呈现明显的规律性。进一步做标准化残差和标准化预测值的Spearman等级相关系数检验，通过表5可以看出，二者的相关系数近似为0，检验概率P值都大于显著性水平0.05。所以认为不存在异方差现象。

图1 异方差检验图

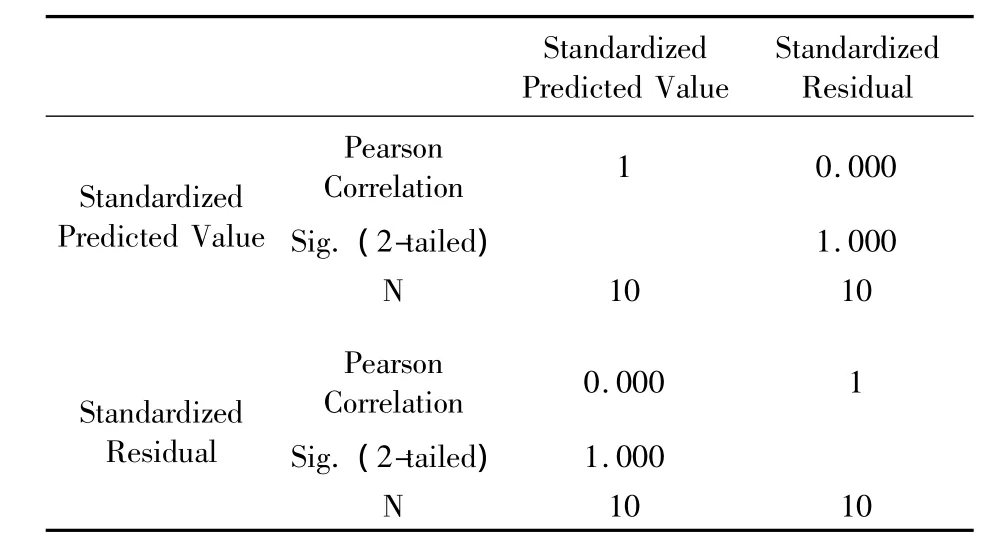
表5 相关性检验

(C)经济意义检验

通过表2，得到的多元线性回归模型为:

由此可知，GDP变化1%时，平均票价变化0.001 967%，并且二者成正比。人均 GDP较大时，说明举办城市比较富裕，消费水平比较高，制定的票价也相对较高。当总投资增加一个单位时，平均票价增加0.011 070 5个单位。投资的越多，票价也会相应的增加。只有这样，才可以有成本的对应补贴。主场容量前面的系数是负的，说明主场容量的大小与票价负相关，即主场容量增大，门票价格递减。因为，场馆容量越大，可以出售的门票越多，每张门票定价相对低，也可以获得很大的收入。赞助费前面的系数为正，说明其与门票价格正相关。这意味着赞助费越高，越能说明该项赛事的受欢迎程度高，可观赏性强，故赛事门票价格就越高。

2.3.3 模型的简单应用 2010年第16届亚运会在广州举办。2010年广州的人均GDP为11 695美元。亚运会的总投资达1 200亿元，共设置了两万个座位，有四个亿的赞助费，见表6。

表6 亚运会相关数据

我们将上述数据带入到模型(1)中，计算得到的最低平均门票价格的估计值为191.235 8。这个数字是能补充成本的最低平均门票价格。举办方为了能获得一定的利润，会在此基础上提升价格，官方发布的亚运会平均票价为200元，这是实现利润后的价格定位。综上分析，在一定程度上表明了模型的可行性。

3 价格差别理论在赛事门票定价中的应用

3.1 价格差别的含义和分类

由于消费者的年龄、职业、性别、偏好、经济状况等情况的不同，他们对同一比赛的需求不同。通常情况下，经济水平较低的消费者，其需求曲线斜率小，门票价格的变动会引起需求量较大幅度的变化;经济水平高的消费者恰好相反，门票价格的变动不会引起需求量的大波动。如果采用单一价格，就会降低对价格变化反应敏感的消费者的购买量，不利于举办方的利润增加，所以有必要实行差别定价。

价格差别[7]是指对同一成本的产品对不同的顾客指定不同的价格，或者不同成本的产品对不同顾客制定统一价格。大多数的体育赛事市场属于不完全竞争市场。只有在不完全竞争市场结构的条件下，举办方才可能依据利润最大化的条件，对消费者实施差别定价。

价格差别主要有三类，并且每一类都有不同的适用条件。

(1)一级价格差别。一级价格差别又称为完全歧视，是指厂商依据每个消费者为每单位商品愿意付出的最高价格，为每单位商品制定的不同的销售价格。在此条件下，每个购买者都能以愿意支付的最高价格获得想要的产品，而厂商成功地获得了全部的消费者剩余，实现了利润的最大化。

在实际的赛事票价定价过程中，一级价格差别很难实现。首先，向每一个消费者收不同的价格是不现实的。因为举办方不可能为每个人制定一个价格去制定门票;其次，消费者通常会保留自己愿意支付的价格底线。所以，在门票定价中，一级价格差别很难应用到实际中。

(2)二级价格差别。二级价格差别又称非线性价格定价。由于单位产品的定价不是固定的，而取决于买者购买数量的多少。厂商将产品分组，按组来制定差别价格。在此条件下，消费者会因购买数量的不同支付不同的价格。一般情况下，购买量与支付价格成反比。在一般的赛事中，厂商通常把门票按包厢、贵宾席、分区票、购票量打折等不同的组别来定价。在实际情况中，二级价格差别确实可以增加举办方的收入。

(3)三级价格差别。三级价格差别是最普遍的价格差别，是指厂商把面临的市场分成若干个不同的分市场，同一种产品在不同的分市场有不同的价格，但在同一市场的价格一致。它是依据各个分市场的边际收入等于总市场的边际收入的原则，把总销售量分配到各个分市场，然后依据各个分市场的价格需求弹性，制定差别价格。

三级价格差别是应用比较普遍的定价方式。其适用条件有:市场必须可以划分区域，每个区域显示出不同的消费区域强度;低价区的门票不可以转让给高价区;提供座位的边际成本近似为零;售出的票量不能超过体育场容量[8]。

下面主要以三级价格差别为定价准则进行门票定价的分析。

3.2 差别定价模型的建立与理论检验

3.2.1 差别定价模型的建立 假设各个赛区分市场是完全垄断的，其需求函数为:Pi=Pi(Qi)

总收入函数为Ri=Pi*Qi

其中，Pi为第i个分市场的门票价格，Qi为第i个市场的消费数量，Ri为第i个市场的总收入。

则边际收入函数为:

成本函数为:

Ci=FCi+ci(Qi)

其中，FCi为固定成本，Ci(Qi)为变动成本，要求很小或变化不大。

边际成本函数为:

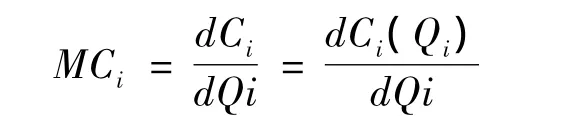
因为Ci(Qi)很小或变化不大，所以MCi近似为零。

所以完全垄断的体育赛事门票定价模型为:

MAXπi=Ri－ Ci

πi为经营者的利润。

经营者利润最大化的均衡条件为

MRi=MCi≈0

由此，可以得到经营者利润最大化时的Qi，即最优的消费票数，并将此数代入到需求函数中，便可得到分市场利润最大化时的门票价格[9]。

用上述方法可以确定各个分市场的门票价格，进而得到的总利润为:

3.2.2 差别定价模型理论检验(见图2) 假设赛事门票进行单一定价，最优价格为P，销售票数为Q。若根据消费差别将消费群体划分为贵宾、普通、学生三个分市场，门票价格分别为 P1、P2、P3，销售量分别为Q1、Q2、Q3。假设在单一定价时，销售的贵宾、普通、学生票数分别为 q1、q2、q3，则 Q=q1+q2+q3。如图2所示，因为在差别定价中，P1、P2、P3与 Q1、Q2、Q3对应的是最佳均衡点，是利润最大的组合点，其他组合点的收益都要比它小。

图2 理论检验

所以

P1Q1+P2Q2+P3Q3≥p1q1+p2q2+p3q3

按照差别定价可以提高门票的收入，使经营者的利润达到最大化[10]。

3.3 差别定价模型的应用与实现

为实现差别定价理论的应用，我们需要按照如下的步骤去做:

(1)划分市场。经营者需要将比赛的消费者按不同的类型划分，进而划分出不同的市场，例如将消费者分为贵宾、学生、老人、普通等。

(2)市场调研。市场调研是经营者获得消费者相关信息的有效途径，可以通过发放调查问卷来实现。实现对消费者的需求估价、兴趣、消费能力以及对现行价格的意见等。

(3)统计分析与确定需求函数。通过之前的市场调研，我们可以获得消费者的有用信息，对其进行统计分析，确定出不同市场的需求函数，再结合成本函数，根据边际收入等于边际成本的均衡条件，确定出各个分市场利润最大化时的票价和数量。

同时，门票差别定价模型一般建立在体育场容量不受限制的基础上。如果提供座位的边际成本近似为零，门票价格满足均衡条件时，可以实现利润的最大化;如果观众的需求超过了球场容量，则经营者的利润将不再增加。

4 结论

本文主要是依据计量模型的方法确定最低平均门票价格，在此基础上提出应差别定价。在最低平均门票定价的计量模型中，依据的是历届奥运相关数据，建立了价格与总投资、赞助费、主场容量和赞助费的多元线性回归模型，并且在模型通过检验的前提下，实现了模型在亚运会赛事票价中的应用检验，据此模型可确定出各大型赛事的最低平均门票价格。进而分析并建立了差别定价模型，并证明了在体育赛事门票定价中应用差别定价，可以帮助经营者实现利润最大化。

综上所述，我们应该在清楚收回成本的最低平均票价的同时，考虑政治、经济、文化以及赛事的影响程度等因素来制定差别票价。本文在建立最低门票定价的计量模型过程中，由于拟合模型数据的有限性，可能导致最后的模型不够精确;在解释变量的选择上，本文只选择了能够定量化的变量，一些不可量化的经济、政治、文化及赛事影响程度等因素也会影响到门票的制定文没有考查。总体来看，本文所建立的模型比较合理，具有可行性，可以为赛事的定价做参考。

[1]于美娜.论我国体育赛事门票定价的影响因素与策略[D].上海:上海师范大学，2007.

[2]吴勇.市场营销[M].北京:高等教育出版社，2011.

[3]史兵，王颖.综合型运动会门票定价理论研究[J].中国体育科技，2003，39(8):6 ～8.

[4]韩开成.价格歧视策略在奥运会门票定价中的运用[J].体育科技文献通报，2005，13(3):48 ～49.

[5]黄道明，王秋萍.基于大型综合赛事门票定价体系的计量模型分析[J].体育科学，2011，31(1):69 ～74.

[6]李子奈，潘文清.计量经济学(第三版)[M].北京:高等教育出版社，2010.

[7]李南筑，袁刚.体育赛事经济学[M].上海:复旦大学出版社，2006.

[8]张连凯.基于消费差别的商业体育赛事门票动态定价模型构建[J].西安体育学院学报，2010，27(4):428 ～440.

[9]勒龙辉，刘平，陈存志.价格歧视理论在我国职业足球联赛门票定价中的应用[J].体育学刊，2002，12(5):20 ～22.

[10]高鸿业.西方经济学[M].北京:中国人民大学出版社，2007.