移动协助传感器网络中Sink的路径优化策略

张希伟，沈琳，蒋益峰

（1.河海大学 计算机与信息学院，江苏 南京 210098; 2.江苏理工学院 电气信息工程学院，江苏 常州 213001）

1 引言

无线传感器网络（WSN, wireless sensor network）中存在能量空洞（energy hole）、冗余覆盖（overlap）和热点（hot spot）等问题[1～3]。尽管可以在基站周围部署更多的节点轮流工作（即离基站近的区域节点密度较大）[3～6]，但无疑会增加网络的成本和计算代价。

在无线传感器网络中引入了移动性，即在Sink节点上配备移动装置可以有效地解决上述问题。通过基站的移动，使负责向 Sink转发的节点经常变化，将网络负载分担到不同的节点上。利用移动节点进行数据收集的一个典型是 Shah等提出的数据骡子（data mule）的模式[3]。近年来在煤矿、森林等传感器网络应用中也出现了利用移动节点来进行数据收集的例子[7,8]。

移动性带来的一个问题是增加了数据的延时。由于移动Sink的运行速度有限（一般为1～2m/s），远远小于无线网络传输的速度，因此，在选择移动Sink传输和无线传输中存在一个折中[9]。例如在图1中，移动Sink综合考虑了能量和延时之间的关系，并不是访问所有的静态节点，而是只访问数据汇聚点（CP, collection point）。静态节点事先将数据发送到汇聚点，当移动Sink到来时再进行转发。文献[10]提出了一种基于旅行商问题的汇聚点选择算法，总是选择那些能够节约最大能量的位置作为汇聚点。文献[11]在此基础上提出了基于虚拟点优先级的移动Sink路径优化方法。同样地，当传感器通信范围内存在多个移动 Sink时，需选择一个合适的 Sink进行数据传输[12]。

图1 一个典型的利用移动Sink收集数据的WSN应用

本文主要研究移动Sink的路径优化策略。通过分析移动路径和网络能耗之间的制约关系，建立优化模型。根据数据采集的不确定性，提出了一种基于访问概率的汇聚节点选择算法。移动Sink按照一定的概率访问汇聚节点，在满足数据收集效率的前提下，该方法可以有效地缩短移动轨迹。

2 网络模型

本文的主要目标是:针对Sink移动轨迹可控的无线传感器网络，综合考虑数据延时和能耗两项技术指标，提出了一种优化的Sink路径选择机制，提高了系统能耗利用率，具体包含以下2个优化目标:

1) 移动距离在满足系统要求的情况下最短化；2) 在目标1) 的基础上，系统整体能耗最小化。首先，定义一个由N个传感器节点和一个Sink节点组成的无线传感器网络，网络是全连通的。节点间采用多跳方式通信；节点具有相同的初始能量，且能量有限，但Sink的能量不受限制；每个节点可以通过 GPS或其他定位算法知道各自的位置信息；Sink节点具有移动性，并且移动方式可控，其以恒定的速度 Vm移动。

采用树形结构来表示网络的拓扑。设移动Sink从节点B出发，并最终回到节点B。令 T( V, E)为以B为根节点的一颗树，其中，V为所有传感器节点，E为这些节点间的连接线。所有源节点的集合S = {Si}⊆ V ；所有CP节点的集合表示为 C ={ p0,…, pnp-1}，pi表示第i个CP节点。当然一个CP节点也是一个源传感器节点。此时，将以每个 pi为根节点形成子树，子树中的每个节点将数据传输给 pi并等待Sink节点来收集数据。用 np和 nnumber来表示CP节点的数量和成员节点的数量。即

2.1 移动路径最短化

利用移动Sink进行数据收集时，数据延时等于数据产生到移动Sink收集该数据的时间差。可以看出，最大数据延时是移动Sink访问所有CP节点所需要的时间。数据延时要求越小，Sink的移动路径越短。

假设在Sink的移动路径上共有 np个CP节点，每一对 CP节点间的直线距离可以表示为 [p0,p1],[p1,p2],…, [pnp-2,pnp-1]，这里可以用{z0,z1,… , znp-2}来表示。对于用户给定的最大数据延时 Dr，应该满足

2.2 系统能耗最小化

本文采用文献[13]中的简化能耗模型，节点总能耗p由接收和发送的数据总量kr和kt来决定。e为常数，表示发送和接收单位比特数据的能耗。如式(3)所示。

当 Sink移动到终点并返回到起点时，称其完成一“轮”移动。在每一轮中，任意节点i接收数据量和发送数据量之间的关系为=+q，q表示节点i在单轮中所采集到的数据总量。故有下式

其中，hi表示节点i到其所属CP节点的最短跳数。如果节点i为CP，则hi为0。根据式（4）可以将单轮系统总能耗ptotal表述为最小跳数和的形式。

其中，pi为任意节点i的单轮总能耗。根据式（5）可知，系统总能耗最小化问题等价于全网节点距离其所属CP节点跳数和的最小化问题。

2.3 最小能耗最短路径问题

根据上述分析，可以发现当选择较长的 Sink节点移动路径时，移动Sink可以访问更多的CP点，使每个以CP点为根节点的子树规模较小，从而节约网络的能耗。但由于移动路径较长，数据传输的延时会增加。相反，要求较小的数据延时，网络的能耗也会变大。因此，在网络能耗与移动路径的长度上存在一个折中，称为最小能耗最短路径问题（MEMD, min-energy min-distance）。Sink移动路径的优化问题可描述为

目标函数

满足约束条件

3 汇聚节点的选择

3.1 问题定义

定义1 （MEMD问题）给定树结构 T( V, E)，由根节点（B）和一组传感器节点 S =⊆ V 组成。寻找一条路径U，从B出发，并访问所有CP节点后回到B。使得路径U的长度不超过规定延时内的移动距离，即 Drvm，同时满足

定理1 MEMD是NP-hard问题。

证明 可以将 MEMD问题规约为一个旅行商问题（TSP, traveling salesman problem）。MEMD问题的一个特例是寻找一条移动路径使得网络的传输能耗为 0。在这种情况下，所有的源节点都必须为CP节点，即移动Sink访问所有传感器节点。此时，可以规约为一种旅行商问题，在规定的时间内访问一组城市并使路径最短。

证毕。

3.2 基于效用的贪心算法

这里给出一种基于效用的贪心算法（utilitybased greedy heuristic）来选择CP节点，称为CPUG算法。该算法总是选择那些能够节约最大网络能量的节点作为CP，并且所有CP节点间的距离和不超过Drvm。因此效用（utility）可定义为该CP节点节约的网络能量与增加的移动距离之间的比值。

需要注意的是，CP节点的功效会随着移动路径长度的变化而变化。如在图2所示，如果移动Sink的路径只能覆盖B和其余一个CP点，即p1、p2或p3，那么应该选择p1，因为有5个源节点在它的子树中，其节约的能量最多。如果移动Sink的路径可以覆盖 B、p2和 p3，所有的数据将在 p2和 p3点收集，p1的效用将为0。因此，CPUG算法必须在Sink的移动过程中动态地更新每一个节点的效用，通过多次迭代执行获得最佳的CP集合。

图2 CPUG算法执行示例

图3给出了CPUG算法的伪代码。初始情况下CP队列中只包含根节点B，通过计算节点的效用不断地加入CP节点。CPUG算法利用TSP()I过程来计算访问集合I中所有节点的最短路径。TSP()I可以采用基于几何结构的旅行商问题求解算法。每次迭代时，首先确定所有的CP候选节点（第2）步）。如果一个节点的加入使得移动Sink以更短的路径访问所有的CP，同时这些CP节点的子树中源节点的跳数和减少，那么该节点可以是一个候选节点。

候选节点x的效用定义为

u(x)等于源节点传输数据时跳数的减少和Sink移动距离的增加之间的比值。CPUG算法选择具有最大效用值的CP候选节点加入到CP队列中（3）和4）），同时将CP队列中效用值变为0的节点清除出去（5））。如果所有的源节点都已在Q中，则结束，否则开始新一轮的迭代。

图3 CPUG—— 一种基于效用的CP节点选择算法

以图2中的例子来说明CPUG的执行过程。图2给出了CP队列，需要3次迭代完成。在第1次迭代过程中选择 s1作为CP节点。第2次迭代中，在所有节点中 s2具有最大的效用值。尽管 s2和 s3在路径的距离增加上是相同的，但 s2节约的能量比 s3多，因为 s3的子树中只有一个源节点，而 s2的子树中有2个。在第3次迭代中 s3也被选择CP节点，同时由于 s1的效用值变为0，将 s1清除出CP节点队列。

4 概率路径选择算法

在 WSN应用中，sensor节点按照一定的duty-cycle进行工作。数据的产生具有时间性。当移动Sink对某个CP节点收集数据时，如果该CP节点没有数据上传，那将造成访问该节点的时间浪费。因此，移动Sink对CP节点可以按照某种概率进行访问，通过概率的变化和移动Sink的数量来保证数据收集的完整性。

4.1 数据延时限制

通常情况下，用户对数据采集的延时会提出要求，例如最大数据延时为 Dr，而系统必须保证数据延时值不大于Dr。设移动Sink访问所有CP节点一次为一个周期，所需要的时间为τperiod。为了实现时间限制，首先给出访问率的定义。

定义2 访问率:一个CP节点在一个周期内被移动Sink至少访问一次的概率定义为该CP的访问率γp。

设某CP节点p的数据传输延时为Dp，则Dp和γp之间存在如下关系。

定理2 Dp的累积分布函数（cdf）如下

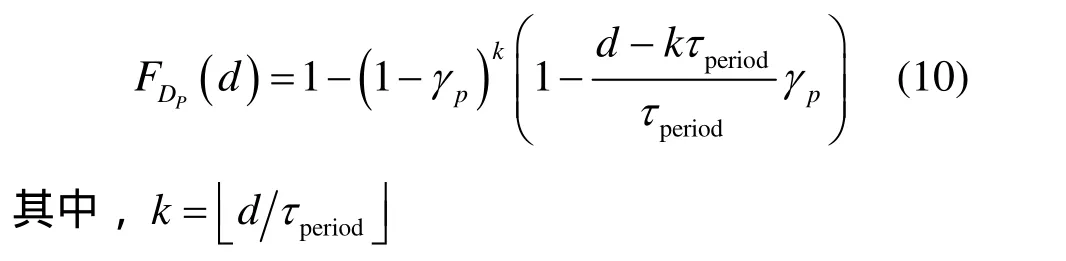
证明 Dp的cdf函数表示为

这表示在时间长度为d的范围内，没有移动Sink访问该节点。共经历了k个τperiod周期以及剩余的d-kτperiod时间。τperiod内未访问该节点的概率为1-γp，d-kτperiod时间未访问该节点的概率为1-γp。

证毕。

根据这个性质，可以得到传输延时的上限。定义CP节点的最小访问率为γ0，其数据传输延时D0应该满足

显然，如果CP节点的访问率大于该最小访问率，那么数据传输延时应更小，即

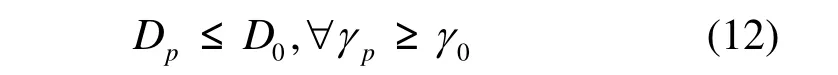
结合式（11）和式（12），可以得到

因此，当确保对每一个CP节点的访问率均大于γ0，那么可以保证所有数据的传输延时都低于用户要求的最大延时Dr。由于对Dr要求的不同，因此γ0也会随之变化。γ0情况下D0的期望如式(14)所示。

定理3 当CP节点的访问率为γ0时，D0的期望为

因此，可以得到D0的期望为

证毕。

上式中可以看出D0的期望值是γ0的单调递减函数。

4.2 基于访问概率的最短路径选择

本文给出了一种基于CP节点访问概率的路径选择优化算法。每个CP节点在系统初始化时分配一个访问概率，该访问概率由最大数据延时、Sink移动路径长度和移动Sink的数量等因素决定，以保证在最大数据延时内获得最长的路径，相应地可以选择更多的CP节点来节约网络能量。

图4给出了一个基于概率访问的简单例子。图4(a)中，移动Sink需要访问5个CP节点。对于每个 CP节点 pi（pi∈C），其访问概率设为βi，而忽略该节点的概率为1-βi。在Sink的移动过程中，要实现平滑的移动路线是很困难的，采用图4(b)中的方法，用节点间的欧式距离作为移动长度。每个连线上的权值即为该节点的访问概率。

图4 概率路径选择问题

结合CP节点的访问概率和欧式距离来处理最短路径选择算法。对于CP队列中每一个CP节点pi，其访问概率为βi，设前一个CP节点到pi节点的欧式距离为 wi，当前系统中共使用了m个移动Sink来收集数据。那么，可以构造整型线性规划（IPL）模型为

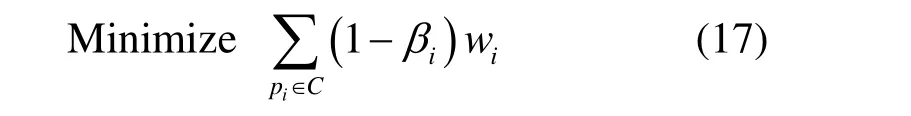
满足约束条件

式（18）确保了CP节点的访问率不低于最大延时需求下的访问率。

本文采用了单一访问概率方法（identical probability schema），在多个移动Sink访问某CP时采用单一的概率，并且在系统的运行过程中不变。可以求出CP节点的传输延时期望与访问概率之间的关系。

定理 4 当对 CP节点采用单一访问概率方法时，其数据传输延时的期望值为

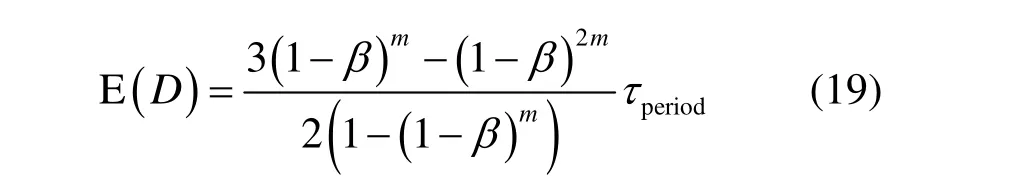
证明 设M为该 CP节点的数据被移动 Sink收集前经过的访问轮数，那么M的概率分布函数为

其中，θ为单轮内CP节点的访问概率，则

将θ代入式（20）中，得

如果数据在第i轮被收集，那么将增加传输延时 （i- 1）τperiod，因此，计算条件M下的期望值为

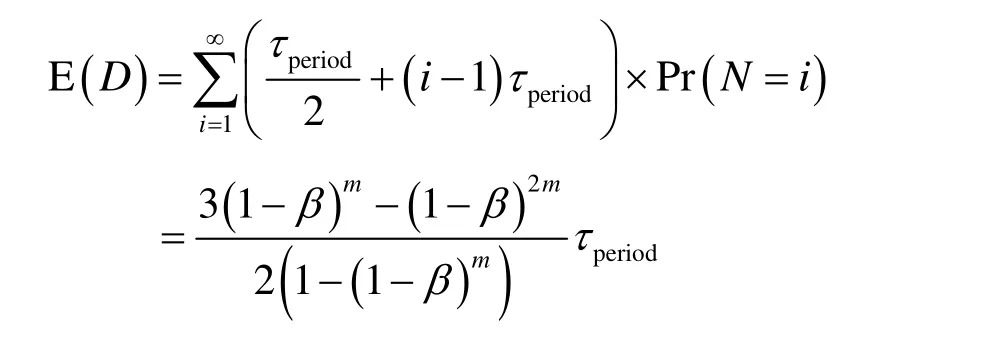
证毕。

5 性能分析

5.1 实验设置

本节采用 NS2模拟器和真实的移动传感器实验床来测试CPUG算法和基于路径选择算法在网络能耗和数据传输延时方面的性能。

在 NS2模拟器中主要测试网络的能耗。设在300m × 300m的区域内随机部署400个节点，并从中选取100个节点作为CP节点。假设移动Sink从区域的左上角出发。源节点以较低的duty-cycle进行数据采集，并传输给CP节点。最大数据延时为5min，那么duty-cycle可在5min以内。

模拟实验采用 C++语言编写。通信规范符合CC2420 协议（Mica2 节点）[14]。传输带宽为 40kbit/s，传输能耗为4dBm。设数据分组的大小为30byte。为了模拟网络链接的不可靠性，采用USC链接层模型[15]。

笔者在室内进行真实的实验床性能测试。如图5所示，在15m×15m的房间内划分成11×11的网格，20个TelosB传感器节点（配置CC2420通信模块）随机放置在这些网格中，每个网格最多放置一个节点。传感器节点使用TinyOS 2.x操作系统，编程语言为nesC。移动Sink节点使用自主设计的DataTruck移动传感器节点[16]。该节点具有强计算能力和大存储容量，采用了32bit ARM处理芯片，配置4个直流电机，最快速度接近2m/s。移动Sink节点如图5(b)所示。

图5 实验环境及移动Sink

5.2 网络能耗

为了便于观察网络的性能，将本文算法和其他2种方法进行比较。一种是未使用移动Sink的情况，即通过多跳协议进行数据传输，称之为NET；另一种是文献[10]中使用的RP-CP算法，它也是一种利用移动节点和汇聚点进行数据收集的方法。首先，测试网络能耗与移动节点速度的关系。从图6中可以看出，随着移动Sink速度的增加，网络能耗逐渐减少。这是因为移动Sink可以在规定的时间范围内收集更多的数据。图6中的CPUG-PPS方法是指利用CPUG并结合概率路径选择算法共同完成数据收集。可以看出CPUG-PPS方法收集相同数据量时所需的能量开销更小，是由于它可以减少更多的时间。如果按照特定的移动路径，CPUG-PPS方法比NET方法节约40%～70%的能量。可以看出移动速度对网络能耗有较大的影响，在下面的实验中固定Sink的移动速度为1.5m/s。

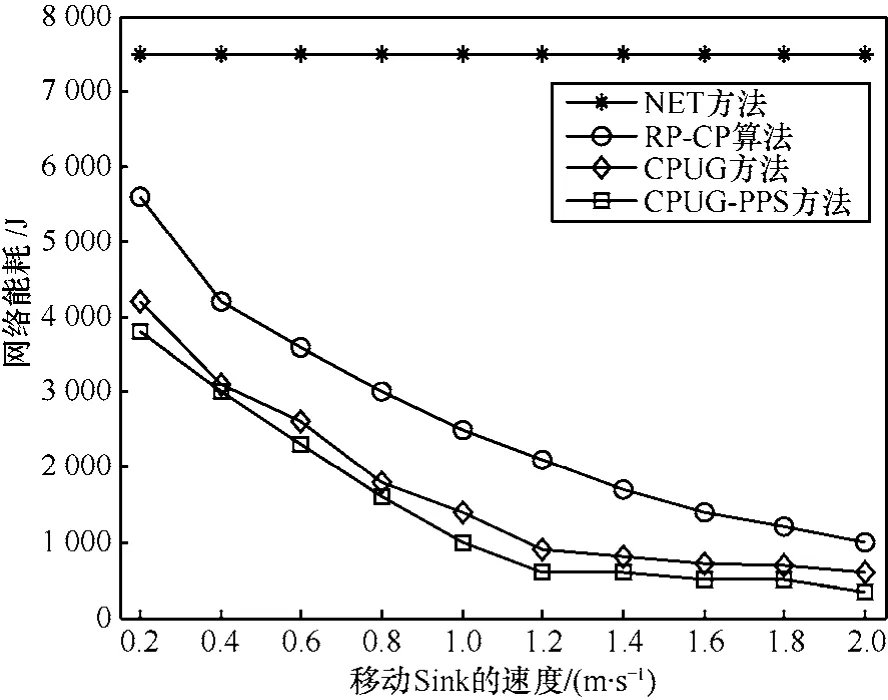
图6 网络能耗与移动Sink的速度关系

图7给出不同节点密度下性能的比较。当节点密度高时，网络的链接性能将会更佳，所以在能耗方面3个算法的性能都优于密度低的情况。同样地，因为 CPUG-PPS方法忽略了一些没有数据传输的CP节点，节约了更多的网络能量。

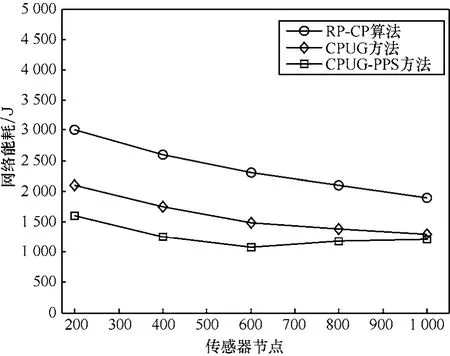
图7 网络能耗与传感器节点的关系

接下来，关注在不同的传输延时要求下算法的性能变化。设有8个不同的时延上限，从5min到40min，每个时延间隔5min。从最低的5min开始，每个条件下的源节点数目相同。从图8中可以看出，随着时延上限的增加，网络的能耗却相应地减少。这是因为在较长的时延上限情况下，算法可以访问更多的CP节点，减少了源节点到CP节点的跳数，从而节约了能量。

图8 网络能耗与延时限制的关系

网络能耗的一个指标是以CP节点为根节点的子树中数据传输的跳数之和。为了方便起见，通过统计所有子树的路由长度来表示。路由长度越长，相应地，数据传输的跳数也越多。图9给出了不同算法下网络中所有子树的路由长度。可以看出，当规定的时延上限增加时，由于可以选择更多的CP节点，因此路由的长度减少了。图10说明了当网络中传感器节点增加时，由于每个CP节点的子树规模也会增加，因此网络能耗也增加了。

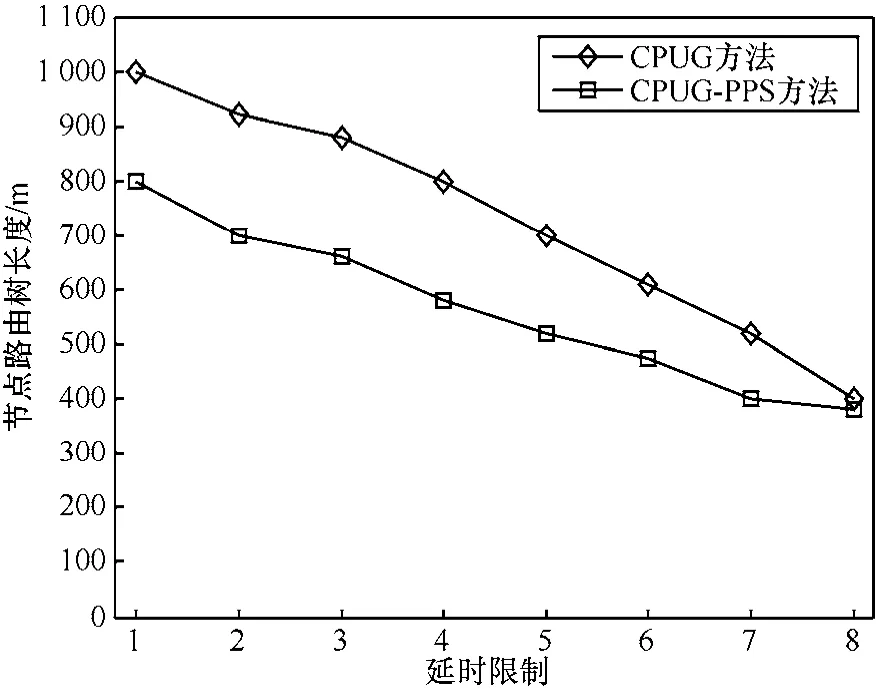
图9 节点路由树长度与延时限制的关系

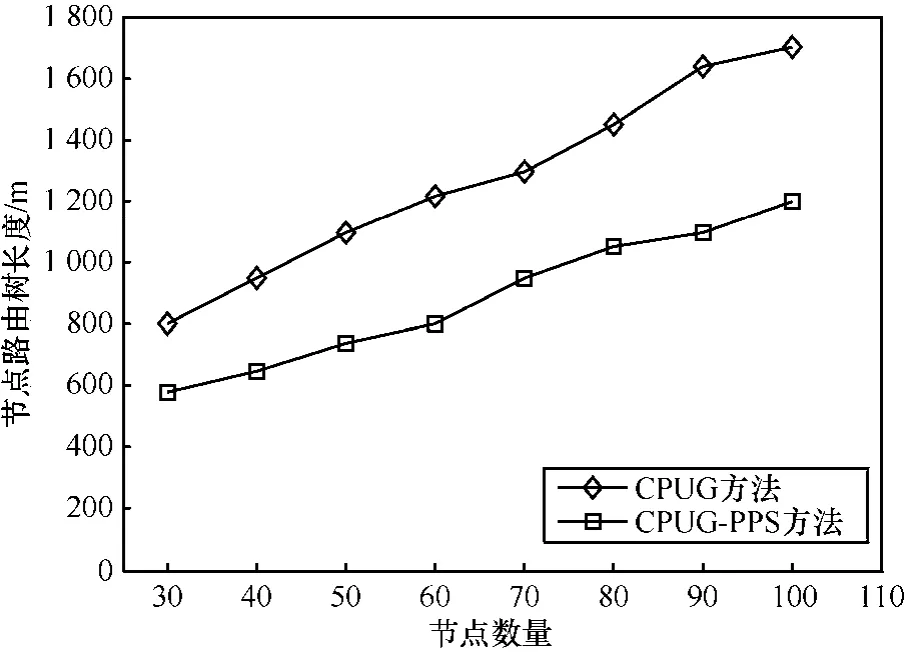
图10 节点路由树长度与节点数量的关系

另一组实验用来测试移动 Sink数目变化时网络的性能。每个移动Sink轮流访问CP队列中的节点，其间隔可根据移动Sink数据的增加相应减少。从图11可以看出，当移动Sink的数目增加时，由于在相同的规定时间内可以访问更多的CP节点，所以网络能耗逐渐减少。

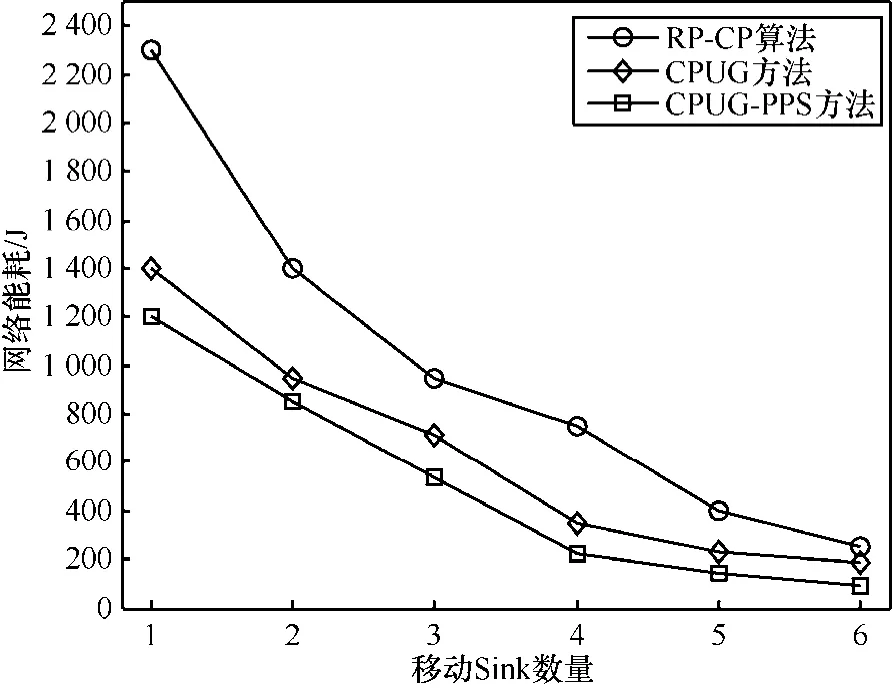
图11 网络能耗与移动Sink数量的关系

5.3 概率路径选择算法性能

利用移动传感器实验床单独测试概率路径选择算法的性能。主要包括2个性能参数，一个是传输的时延，一个是路由树的长度。

为了标识网络中的每个节点，节点必须具有唯一的地址以及特定的数据传输格式。节点地址可以用数字来表示，传输格式如图12所示。

字段的含义如下:

实验中选择5个节点作为CP节点，其他作为源节点。移动Sink按照一定的概率访问这5个CP节点。通常情况下移动Sink以闭环的方式循环访问这些CP节点，通过测量可知这 5个节点间的最短距离为50m，那么平均延时为25s左右。图13给出了CP节点的访问概率与平均传输延时之间的关系。从图13中可以看出，移动Sink根据访问概率会避免访问一些 CP节点，减少了移动路径，因此缩短了传输延时。图14中的曲线说明了当一些 CP节点没有访问但其有数据需要传输时，在最大延时之前通过多跳的方式发送到基站，这样增加了网络能量的开销，所以随着访问概率的降低能耗会增大。

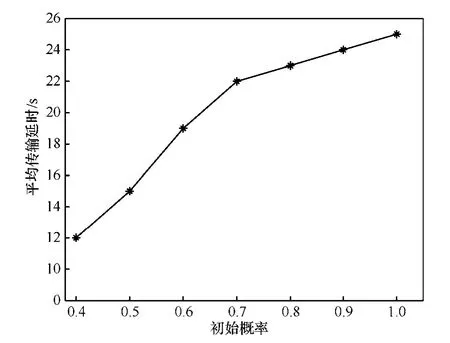
图13 平均传输延时与初始概率的关系

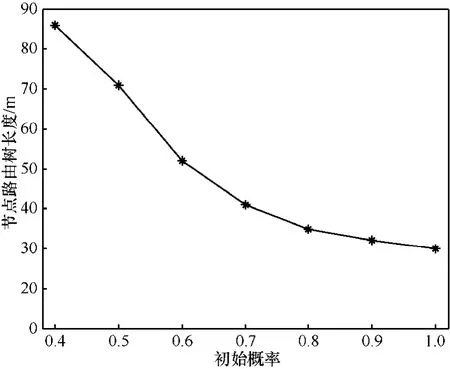
图14 节点路由树长度与初始概率的关系

在第2组实验中，假设20个传感器节点均为CP节点，当一个移动Sink访问这些节点的概率均为80%，那么它在2轮中对这些节点的访问情况如图15所示。可以看出在这两轮中，移动Sink访问90%以上的节点。因此，可以说当对 CP节点确保相对较高的访问概率时，绝大部分的节点可以在较少的时间内访问到。

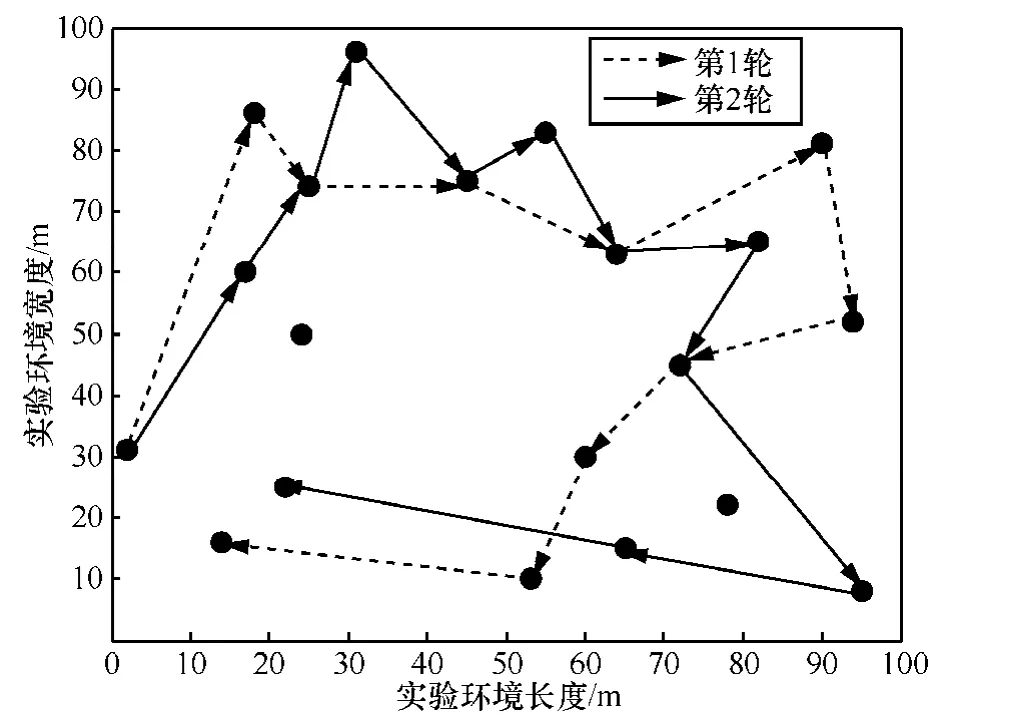
图15 单个Sink在2轮移动过程中的路径选择情况

6 结束语

本文利用移动Sink来解决WSN中能量空洞等问题。提出了一种最短移动距离最小能耗的路径优化算法，并证明了该模型是一个NP-hard问题。为了在规定的最大传输延时范围内访问尽可能多的CP节点，提出了一种基于CP节点访问概率的路径选择算法。通过模拟实验以及实验床的真实数据，验证了本文提出的算法能够很好地在满足延时要求的同时节约网络的能量。

[1]TOLLE G, POLASTRE J, SZEWCZYK R, et al.Amacroscope in the redwoods[A].ACM SenSys[C].San Diego, USA, 2005.51-63.

[2]MAYER K, ELLIS K, TAYLOR K.Cattle health mon-itoring using wireless sensor networks[A].Proc of the ACM IASTED[C].Cambridge, Massachusetts, USA, 2004.375-380.

[3]XUE W, LUO Q, CHEN L, et al.Contour mapmatching for event detection in sensor networks[A].Proc of the ACM SIGMOD[C].Chicago, USA, 2006.375-380.

[4]DU W, FANG L, NING P.Lad:localization anomaly detection for wireless sensor networks[A].Proc of the IEEE IPDPS[C].Denver,Colorado, 2005.121- 127.

[5]ASLAM J, BUTLER Z, CONSTANTIN F, et al.Tracking a moving object with a binary sensor network[A].Proc of the ACM SenSys[C].San Diego, USA, 2005.150-161.

[6]SRINIVASAN W W V, CHUA K C.Trade-offs between mobility and density for coverage in wireless sensor networks[A].Proc of the ACM MobiCom[C].Montreal, Quebec, Canada, 2007.39-50.

[7]LI Z J, LI M, WANG J L, et al.Ubiquitous data collection for mobile users in wireless sensor networks[A].Proc of the IEEE INFOCOM[C].Shanghai, China, 2011.2246-2254.

[8]LUO J, ZHANG Q, WANG D.Delay tolerant event collection for underground coal mine using mobile sinks[A].Proc of the IEEE IWQoS[C].Charleston, USA, 2009.1-9.

[9]SUGIHARA R, GUPTA R K.Optimizing energy-latency trade-off in sensor networks with controlled mobility[A].Proc of the IEEE INFOCOM[C].Rio, Brazil, 2009.1398-1408.

[10]XING G L, WANG T, JIA W J, et al.Rendezvous design algorithms for wireless sensor networks with a mobile base station[A].Proc of the ACM MobiHoc[C].Hongkong, China, 2008.231-240.

[11]郜帅, 张宏科.时延受限传感器网络移动 Sink路径选择方法研究[J].电子学报, 2011, 39(4):742-747.GAO S, ZHANG H K.Optimal path selection for mobile Sink in delayguaranteed sensor networks[J].Acta Electronica Sinica, 2011,39(4):742-747.

[12]程龙, 陈灿峰, 马建.无线传感器网络中多移动 Sink的选择策略[J].通信学报, 2008, 29(11):12-18.CHENG L, CHEN C F, MA J.Selection schema of mobile Sinks in wireless sensor networks[J].Journal on Communications, 2008, 29(11):12-18.

[13]KIM H S, ABDELZAHER T F, KWON W H.Dynamic delay- constrained minimum-energy dissemination in wireless sensor networks[J].ACM Transactions on Embedded Computing System, 2005,4(3):679-706.

[14]CROSSBOW.Mica and mica2 wireless measurement system datasheets[EB/OL].2004.

[15]ZHAO J, GOVINDAN R.Understanding packet delivery performance in dense wireless sensor networks[A].Proc of the ACM SenSys[C].Los Angeles, USA, 2003.311-320.

[16]张希伟，陈贵海.基于SDMA应用的移动Sink节点的设计与实现[J].计算机研究与发展, 2012, 49(3):541-549.ZHANG X W, CHEN G H.Design of mobile Sink node for SDMA applications in WSN[J].Journal of Computer Research and Development, 2012, 49(3):541-549.