融合面积估算和多目标优化的硬件任务划分算法
2013-10-26陈乃金江建慧
陈乃金,江建慧
(1.同济大学 软件学院,上海 201804;2.安徽工程大学 计算机与信息学院,安徽 芜湖 241000)
1 引言
近年来,随着VLSI技术的迅速发展,尤其是大规模高性能可编程器件的出现,促进了可重用芯片实现的多样化,从而在很大程度上影响了计算机软硬件计算平台的重新定位。可重构计算 (RC,reconfigurable computing)是一种融软件的编程灵活性和硬件的高效性于一体的计算方式。根据应用的不同需要对可重构硬件进行动态配置,根据配置信息来改变其内部可重构单元的功能和相互之间的连接关系,并在辅助设备(包括外围控制硬件和软件)的协同下完成相应的计算任务,这种系统已经在很多领域得以广泛应用[1~4]。音、视频的编解码等计算密集型任务的关键循环占用了大量计算时间,如果将计算密集型任务经过软硬件划分,然后提取出其关键循环的数据流图(DFG, data flow graph),并将其划分映射到可重构单元阵列(RCA, reconfigurable cell array)上执行,这将大大加快计算密集型任务的执行效率,但是RCA的资源有限,所以在动态可重构系统中,当要计算的硬件任务所需的资源大于硬件能够提供的资源时,就必须要对其进行划分,划分是映射的前提,并且可以直接形成粗粒度可重构处理单元(RPU, reconfigurable processing unit)流水化映射[5~8]的装载调度队列,其结果直接影响从计算密集型任务提取的核心循环在RPU上执行速度。
2 相关研究
传统的 DFG时域划分算法根据电路的抽象层次可大致分为网表级时域划分和行为级时域划分 2类算法。网表级时域划分算法针对的是电路。基于网络流的网表级时域划分算法将电路定义为一个网络流,它可表示为由门和寄存器所组成的节点集、由门和寄存器之间的连接所组成的边集,以及由门和寄存器的面积所组成的面积等3个集合所构成的三元组。而一个计算密集型任务或程序的关键循环可以用 DFG表示,图中每个节点表示一个操作符(或运算符),对这样的图所进行的时域划分通常称为行为级时域划分。
本文研究行为级时域划分方法。文献[9]首次直接讨论了面向可重构计算机系统的硬件任务划分问题,并提出了2个经典的单目标时域划分算法,即层划分(LBP, level based partitioning)和簇划分(CBP, cluster based partitioning),LBP算法在某一硬件面积约束基础上,对计算任务节点进行按层划分。优点是试图获得较大的并行度,其目的是试图获得一个任务 DFG的所有划分块执行延迟总和的较小化,缺点一是划分块间的通信成本较大(表现为一个任务DFG划分块间的非原始I/O边数较多);二是不能根据实际划分情况动态调整就绪列表队列,结果产生了大量硬件碎片;三是把第0层的输入作为第一个划分块,这样做有可能会使任务DFG执行延迟的增大。CBP算法试图尽可能地将联系紧密的操作放到一个划分块中,其目的是想获得划分后DFG块间的较小非原始I/O边数。缺点一是任务DFG的每个划分块内部计算任务节点的并行度较小;二是不能根据实际划分情况动态调整就绪列表队列;三是把第0层的输入作为第一个划分块不太合理,理由同LBP算法。
簇层次敏感的划分(LSCBP, level sensitive cluster based partitioning)算法对CBP算法进行了改进[10],提高了硬件资源的利用率,效果良好,但是该算法缺点一是划分块间的边数仍然较大;二是当一个划分块间运算节点的输出边数超过1时,直接按实际边数进行统计,这样做可能导致该运算结果被多次存储;三是把第0层的输入化为第一个划分块不太合理,理由同LBP算法。
基于流网络的多路任务划分(NFMP, network flow−based multiway−task partitioning)算法是追求划分块间边数较小化的单目标时域划分算法,NFMP算法首先运用了最大流最小割理论计算获得待划分任务 DFG可行的最小割集初始划分[11],然后在此基础上,通过划分子图构造、广度优先搜索和最短路径等相融合来获得划分块间通信成本的较小化(表现为一个任务DFG划分块间的非原始I/O边数较少),效果较好。但是该算法缺点一是在某一硬件资源面积约束下,对待划分任务 DFG所需的划分块总数考虑不足;二是没有考虑每个划分块内运算任务节点的并行度。
现有的典型多目标时域划分算法主要有多目标时域划分(MOTP, multi objective temporal partitioning)[12]、增强的静态列表(ESL, enhanced static list)[13]等。
MOTP算法试图尽可能地考虑划分块数、划分块内运算节点的并行度和划分块间的通信量等3个指标来进行任务DFG的时域划分。优点是获得了较小的划分块数。缺点一是在每次划分时,没有进行硬件资源面积的估算,可能产生硬件碎片;二是统计划分块间输出边的数量不太合理,理由同LSCBP算法。
ESL算法考虑了任务DFG块之间的通信代价和模块关键路径等指标。其不足是对并行因素考虑不够,且没有考虑任务 DFG划分中可能产生的硬件碎片问题。
本文在综合考虑了一个计算任务 DFG划分块数最小化、所有划分块执行延迟总和、所有划分块之间的I/O边数的较小化等3个方面的因素,提出了一种融合面积估算和多目标优化(AEMO, area estimation with multi−objective optimization)的硬件任务划分算法。
3 问题定义
本文的研究有 3个前提条件[14]:1) 待划分的任务由 DFG表示,一个计算密集型任务已经转换为一个DFG;2) 划分块数等于RPU中的RCA重复使用的次数,任一划分均可按划分形状直接映射到一块RCA上去,并且一个划分对应一块RCA,如图1所示;3) 划分算法只考虑硬件实现的计算延迟,而不考虑互连延迟。
定义 1[14]一个计算任务或程序的 DFG是一个有向无环图,可以表示为G=(V, E, W, D),顶点集V= {vi|vi是有序运算符,1≤i≤n},|V|=n表示运算符的个数;边集 E={eij|eij=<vi,vj>,1≤i,j≤n},eij表示从vi到vj的有向边,vi是vj的直接前驱节点,vj是vi的直接后继节点,其表示了vi和vj2个运算符的先后依赖关系,vj的执行依赖于vi,|E|=m为边的数量;权集W={wi|表示vi所占的硬件资源面积,1≤i≤n};D代表延迟集,di∈D代表第i个运算节点的执行延迟。
一般而言,RPU中的RCA的面积为一个定值(表示为ARPU),任意一个任务DFG很难被全部映射上去,这就需要对其进行划分。
定义2 一个DFG的划分问题可以描述如下。
输入:G=(V, E, W, D);ARPU。
输出:G的一个划分P={P1, P2, …, PM}。
约束条件:
目标:1) 划分块数的最小化;2) 所有划分块执行延迟总和的较小化;3) 尽可能减少划分块间I/O边数。
定义3 若一个任务DFG存在一个划分,划分块之间严格按时间顺序执行,它的所有划分块之间如有一个产生了非法依赖关系,则该划分就称为不合理的划分。
设v是一个计算任务或程序的DFG的有序运算符中的任一个运算节点,则v被划入一个划分块的前提是v的所有的前驱节点均已经被分配到相应的划分块中。一个合理的划分要求划分块之间均不产生非法依赖关系。因DFG是一个有向无环图,如果一个节点的前驱节点被分配到其后继模块中,就会引发非法依赖关系现象。图2给出了这种情况的一个例子,为了简化问题描述,假设一个任务或程序的 DFG中各个节点的权值相同,这样,本文可以将面积的单位等价于节点的个数。若ARPU=2,获得P1、P2、P33个划分,设P3总是最后执行,但如果划分块 P1和 P2的执行次序是从 P1→P2,因 P1划分中运算节点 v4前驱v2位于P2划分,所以划分块 P1和P2之间产生了非法依赖关系。

图2 一个不合理划分的例子
4 AEMO算法
4.1 AEMO算法设计
设待划分DFG的运算符节点列表queuelist={v1,v2, v3,…, vn},从列表队列节点里挑选出优先级高的运算节点构成新的就绪列表 readylist={v1′, v2′,v3′,…,vn′},每次划分时依次从 readylist中挑选节点。AEMO算法采用以下5个策略来进行任务划分。
策略 1 可重构划分面积逻辑容量估算和按权值调度划分同时进行,获得最小的划分块数。
下面给出2种实现方案。
1) 方案1 在一个ARPU的约束下,采用的策略是从就绪队列(由入度为 0的点组成)中选取运算节点权值最小(本文约定节点的权值越小,则该点优先级就越高)的点作为起点,按深度优先搜索(DFS,depth first search)进行预划分,获得了一个合理划分,并计算硬件碎片面积 area1=ARPU−area_filled1(其中 area_filled1表示所有划入当前块节点的面积累加和);然后再以同样的起点按广度优先搜索(BFS, breadth first search)进行预划分,获得了一个合理划分,并计算硬件碎片面积 area2=ARPU−area_filled2;将area1和area2进行大小比较,如果area1小,则本次划分按DFS方式进行,否则按BFS方式进行,但是这样做可能有一个缺陷,若 area1=area2,且DFS和BFS一遇到不满足要求的节点就停止,则这样会导致划分方式的不明确。
例1 假设算术表达式中允许包含2种括号:圆括号和方括号,其嵌套的顺序合理,则一个算术表达式可表示为:y=[[[(a×b×k−(g+h))+(c×d×l−m)]%[((a×b)+(e×f+(i+j)))+n]+o]+[[[(a×b+k−(g+h))+(c×d×l−m)]+[((a×b)+(e×f+(i+j)))+n]+p]×[[[(a×b×k−(g+h))+(c×d×l−m)]%[((a×b)+(e×f+(i+j)))+n]]+[[(a×b+k−(g+h))+(c×d×l−m)]+[((a×b)+(e×f+(i+j)))+n]]]]]+[[[(a×b+k−(g+h))+(c×d×l−m)]+[((a×b)+(e×f+(i+j)))+n]+p]+[[[(a×b×k−(g+h))+(c×d×l−m)]%[((a×b)+(e×f+(i+j)))+n]]+[[(a×b+k−(g+h))+(c×d×l−m)]+[((a×b)+(e×f+(i+j)))+n]]]−q],该算术表达式的 DFG如图 3(a)所示,其层次为 9,原始输入边有17条,原始输出边有 1条,非原始输入输出边数为29条,有23个运算任务节点,其集合V={vi|1≤i≤23},划分前P=Φ,划分后P={P1,P2,…,PM},设ARPU=65,则按 DFS (P1={v1,v6},如图 3(b)所示 )或者 BFS(P1={v1,v2},如图3(c)所示)进行预划分获得的硬件碎片均为area1= area2=65−54=11,虽然v3、v4均有划入的可能,但是却不能划入。为此引入第2种方案。
2) 方案2 在一个ARPU的约束下,从就绪队列中按权值选取优先级最高的点作为起点,按DFS进行划分,每划分一次,就更新该点后继节点的入度,如果入度为0就直接预划入,如果入度不为0,考察该点的其他没有划入当前块的前驱能否划入,如果能,则一并预划入,直到没有节点可以填入area_filled1为止,这样就获得了一个DFS的合理划分,计算 area1=ARPU−area_filled1,若 area1<value(value为一设定的阈值,其范围为(0,10],本文设为10),则本次划分按DFS进行,然后计算没有划入就绪点的探测函数值,再按ARPU和权值大小贪婪划入可以划入的点(详细的实现细节见后面的例子说明),否则按BFS进行权值层贪婪划分,即使某个节点的后继入度更新为0,也不直接划入当前块。这样做的目的是尽可能保证每次划分均能最大化利用ARPU,同时增大一个划分块内的运算节点的并行度。
由上可知,策略1侧重于要求每次划分尽可能填满每一块RCA,从而使任务DFG总的划分块数达到最小,而且按BFS进行权值贪婪划分时,考虑了划分块内运算节点的并行度。
策略 2 执行延迟大优先(EDTLF, execution delay time long first)和可重构运算阵列面积的充分利用相融合。
当有多个节点处于就绪状态时,运用“尽可能早”原则,在保证DFG获取合理划分的前提下,优先选择执行延迟大和占用硬件面积大的运算节点。在延迟相同的前提下,占用硬件面积越大的任务越优先,而在占用硬件面积一样的前提下,延迟越大的任务越优先。在遇到当前点不能划入当前块时,还要动态考察该点之后还有无可以划入当前块的点,如有将其贪婪划入,这样做的目的是优先响应执行延迟大节点的同时,又充分利用了可重构运算阵列面积。
由上可知,策略2侧重于同时考虑了硬件碎片利用、硬件划分的吞吐量、执行延迟大节点的优先响应等因素,其目的是想同时获得任务 DFG划分块数和所有划分块总的执行延迟的较小化。
策略 3 优先选择优先级高的节点和当前层任务节点。
在满足资源面积和前后依赖约束的前提下,优先选择优先级大的当前层任务节点,当前层的下一层节点滞后选择;在2个任务节点优先级相同的情况下,优先选择当前层就绪的节点,若不存在这样的点,则按先来先服务(FIFO, first in first out)原则执行;对于同时就绪的任务节点,则选择优先级高的任务节点。

图3 解释方案1不合理的例子
由上可知,策略3侧重于考虑任务DFG划分块内运算节点的并行度。
策略4 尽量减少划分块之间的I/O边数。
实现策略4的方法有:1)每次划分首先按DFS的方式选择当前优先级最大的节点作为起始点划入当前块,同时更新该点直接后继的入度,如后继的入度为0,在满足ARPU的前提下,直接预划入当前块;如后继的入度不为 0,还要考察该点没有划入当前块的前驱能否划入,如果能,则一并预划入;2)每划入一个点,就动态计算正在划分的模块与就绪节点之间的边数,边数越大就说明该就绪节点与当前划分块联系越紧密,尽可能将其划入将有助于减少划分块之间的I/O边数。
由上可知,策略4在策略1~策略3的基础上,侧重于减少划分块之间I/O边数。
策略5 其他方面因素的考虑。
1) 层次大优先级高的节点应优先响应
对于不同层的任务节点要考虑其层号,这样做的目的一方面是在同等条件下,节点的层号越小越优先,另一方面是为了照顾优先级高且层次较大任务节点被优先响应,以便尽可能提高每个划分块内部运算任务节点之间的并行度。
2) 优先划入出度较大的运算节点
同等条件下,优先划入出度较大的运算节点,目的是搜索范围的扩大化使更多的节点成为就绪点,从而有可能使每次划分得以进一步优化。
3) 防止划分块间运算任务节点非法依赖关系的产生
任务DFG的时域划分要求入度为0的点或者某点的所有前驱已经被划入当前块或上一块时才能划入该点,这应在程序中用条件语句加以约束,这样做的目的是防止划分块间非法依赖关系的产生(如图2所示)。
由上可知,策略5中的1)侧重于考虑任务DFG划分块内运算节点的并行度;策略5中的2)侧重于优化每次划分;策略5中的3)侧重于防止任务DFG每个划分块之间产生非法依赖。
根据以上策略,AEMO为就绪列表中的任务构造了新的探测函数(本文约定函数值越小优先级越大),并且根据不同参数指标的贡献大小而将其设为分母或分子。
为了便于实验比较,本文用重构硬件资源面积作为约束条件,各类运算所占的重构硬件资源数(单位:CLB)的确定参照了XC4000E系列8bit FPGA(如表1所示)。
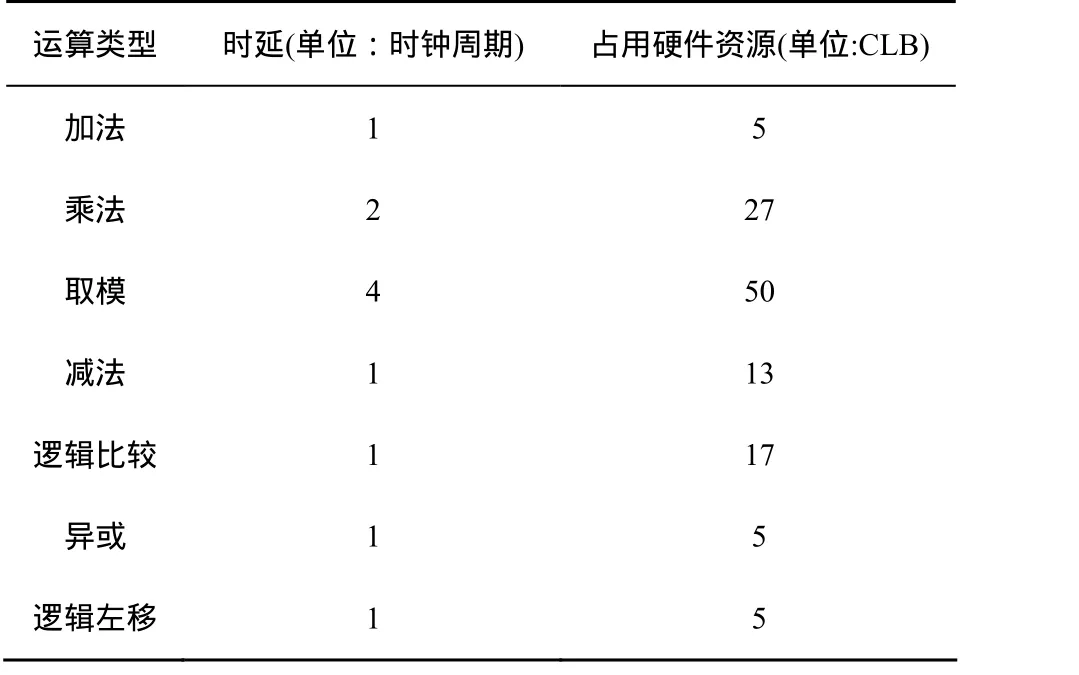
表1 各类运算的时延和占用资源量
探测函数构造的基本思想如下。
首先,由表1可知,运算任务节点执行延迟大,其所占的硬件资源数也较大,故为了保证其优先响应,应采用第i个运算节点vi所占的硬件资源面积wi和其执行延迟di的累加和作为探测函数的分母的一部分(1≤i≤n)。
其次,在任务 DFG的划分过程中,为了尽可能地划入与正在划分模块紧密联系的就绪节点,需要动态计算当前正在划分的模块与就绪节点之间有向边的数量,其目的是尽可能地减少划分块间非原始I/O边数。
例 2 图 4(a)给出了一个正在划分的部分DFG,假设v1和v2点已经被划入到P1中(如图4(b)所示)。现考察就绪节点v3和v4,设v3和v4运算类型相同且位于同一层,在 ARPU的约束下,P1还可以划入 v3或 v4点中一个,P1与 v3的边数为 1,与v4的边数为2,P1划入v3的情形如图4(c)所示,P1划入v4的情形如图4(d)所示,但是图4(d)的方案要优于图 4(c),原因是图 4(c)的划分块间边数为 3,而图4(d)的划分块间边数仅为2。
因此,每次在线动态划分时可将当前正在划分的模块与就绪节点之间有向边的数量(用 s表示)作为探测函数的分母的一部分。
第三,在任务DFG的划分过程中,为了达到当前层任务节点和层号小的节点被优先响应,可将任务节点层次号作为探测函数分子的一部分。但是这样做有时会使层次大的优先级高任务节点得不到及时响应。图 5所示的例子说明,设 v6为加法,v666为乘法,v666的优先级本应高于v6,但v666所在的层次远大于 v6,同时就绪时,为了保证 v666先执行可以在任务节点层次号前面乘以一个修正系数,其最大值定为1/maxlevel,这样可以使层次大的优先级高节点优先得以响应,从而提高划分块内部的并行度。
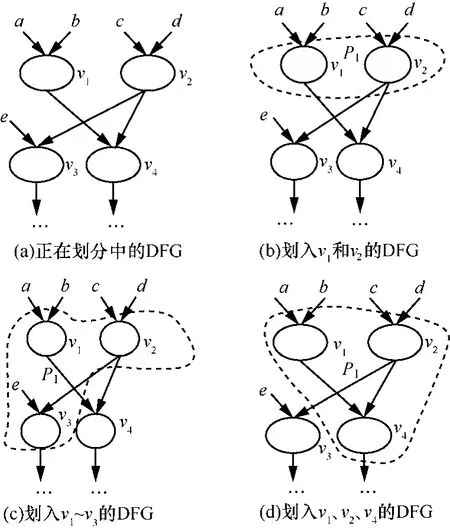
图4 说明计算正在划分的模块与就绪节点之间的边数s的例子

图5 解释优先级高且层次较大节点优先响应的例子
最后,在进行任务 DFG时域划分过程中,待划的就绪列表节点的前驱可被划入当前块或已经被划入到上一个划分中了,所以任务节点被调度时其入度必须为0,这一点可有条件判断语句来实现。但是出度大的任务节点被动态划入当前块时,会使更多的点成为就绪点,选择节点的空间增大有可能优化划分。图6所示例子说明,v1和v2的优先级相同,若按FIFO先划入v1,则只能使v3成为就绪点,但是另外一种可能的方法是先划入v2,这样可以使v4~v9同时成为就绪点,从而可能优化划分。所以可以将任务 DFG的每个节点的出度设定为探测函数的分子或分母,同时为了进行动态调整可以设定一修正系数。
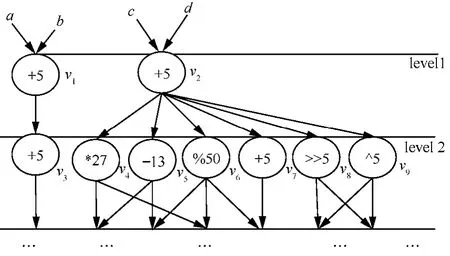
图6 解释出度大的点被优先划分的例子
这样,对于任一个运算节点 vi,其探测函数prior_assigned(vi)可以设定为如下2种形式之一
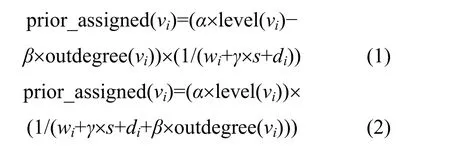
其中,outdegree(vi)表示节点 vi的出度,式(1)把outdegree(vi)作为分子并要做减法,因为分母相同的情况下,分子越小函数值越小,prior_assigned(vi)越小越优先;同理,式(2)把 outdegree(vi)作为分母并要做加法,目的是使分母变大。函数的其他参数说明如下:maxlevel表示一个 DFG的最大层号;maxoutdegree=max{outdegree(vi), 1≤i≤n};maxinputoutputside表示一个DFG非原始输入输出边数之和;level(vi)表示节点vi的层次数,α、β和γ为调整系数,α取值范围为[0,1/maxlevel],β取值范围为[0, maxoutdegree],γ取值范围为[0, maxinputoutputside]。prior_assigned(vi)的值越小表示 vi的优先级越高,即被划入某个划分的可能性就越大。
为了验证相关划分算法,构造了一组划分基准程序集。它们由2部分构成,一是由LBP和CBP算法所用的基准中值滤波器MEDIAN、二叉树比较器 BTREE32、一维离散余弦变换 8次展开 DCT8和4×4矩阵运算MATRIX4、MOTP算法所用的基准二阶差分方程SODE、快速数据加密算法FEAL、快速离散余弦变换FDCT、快速离散余弦变换6次展开 FDCT6、椭圆波形滤波器EWF、椭圆波形滤波器6次展开EWF6,此外还增加了快速傅里叶变换4次展开FFT4(fast Fourier transform 4)、快速傅里叶变换8次展开FFT8(fast Fourier transform 8)2个基准,这些基准的操作单元数量如表2所示。第2部分基准程序采用了文献[14]中列出的且与 ESL和LSCBP所用基准特征相同的10个随机图。程序的开发环境是VC++6.0,运行环境是Windows XP,PC的处理器为Intel(R) Core(TM) i3 CPU, 主频为2.26GHz, 内存为2GB。

表2 划分基准程序集
随机选取的ARPU分别为56 CLB、64CLB、75 CLB,取 α=1/maxlevel,β=γ=1,统计划分块间输出边的数量时,如块间一个运算节点的输出边数超过1,也只算一条边,这样做的理由是避免划分块间同一个节点的运算结果被多次存储。设M表示一个DFG的划分块数,SD表示一个DFG所有划分块执行延迟总和,N表示一个DFG所有划分块之间的非原始I/O边数。
AEMO算法描述如图7所示。
4.2 算法时间复杂度分析
AEMO算法在执行前,一个 DFG总的运算节点数、每个运算节点的执行延迟、运算类型和占用的资源数,每个节点前驱与后继的个数及列表均已知。
设一个DFG有n个运算节点,assign_level()求出每个运算节点层次及该DFG的最大层次号,时间复杂度为O(n2);每次划分所用到的就绪任务节点,在入队时均要通过探测函数 priority_assigned()计算其优先级,其时间复杂度为O(n2);用快速排序函数quicksort()对每次计算出的探测函数值按从小到大排序,其最好情况时间复杂度为 O(n),最坏情况为 O(n2),平均时间复杂度为 O(nlog2n);用函数edges()求一个划分后的DFG块间总的非I/O边数,时间复杂度为 O(n2);假如一个DFG被划分为M块,用直接递归调用来求一个划分后的DFG所有模块执行总延迟函数 delays()的时间复杂度为O(Mn)。

图7 AEMO算法
AEMO算法在对DFG进行划分时,首先要找到当前优先级最高的待划分节点,故每次在划分前通过探测函数计算每个就绪节点优先级的值并排序,找到优先级最高的待划分节点放入当前的划分中,这是一个循环迭代的过程,加上判断 DFG的运算节点是否全部被划分完的约束,共耗费的时间复杂度为O(n4log2n)。综上,AEMO算法的平均时间复杂度为O(n4log2n)。
为了比较2个探测函数的优劣性,AEMO算法分别用式(1)和式(2)实现,再用如表2所示的划分基准程序集进行了实验,结果如表 3所示,其中AEMO1算法采用的探测函数是式(1)。表3分别给出了ARPU=56、64和75时划分基准程序采用2个不同划分算法所得到的划分结果,对应于每个指标(M、N、SD)下每个划分算法和改进的百分比(Δ%)所列出的3列内容。以SODE为例,当ARPU=56时,采用 AEMO1算法所获得的 M=5,而采用 AEMO算法所获得的 M=4,因此,Δ%=−20.0%(负值表示改进)。通过对比可知,用式(2)所获得的结果符合本文的目标,即 M 要最小化,同时获得一个较小SD,且尽可能减少N。因此,本文的后续工作均基于采用式(2)探测函数的AEMO算法。
4.3 一个算术表达式划分实例分析
针对图3(a)算术表达式的DFG,划分前节点有23 个,设 ARPU=65,maxlevel=9,α=1/9,β=γ=1,面积填充变量 area_filled=0,硬件碎片面积变量area1= 0(按DFS),value=10,图8和图9给出了根据AEMO算法每一个步骤的划分子图。
1) 图 3(a)入度为 0的就绪节点为 v1~v5,w1=w2=w3=27,w4=w5=5,d1=d2=2,d3= d4= d5=1,就绪节点v1、v2、v3、v4、v5与当前正在划分的模块有向边的数量均为0,level(v1)= level(v2)= level(v3)= level(v4)=level(v5)= 1,outdegree(v1)=2,outdegree(v2)= outdegree(v3)= outdegree(v4)= outdegree(v5)=1,prior_ assigned(v1)= (α×level(v1))× (1/(w1+ γ×s+d1+ β× outdegree(v1))=((1/9)×1))×(1/(27+1×0+2+1×2))≈0.0036,同理,prior_assigned(v2)= prior_ assigned(v3) ≈0.0037,prior_assigned(v4) =prior_ assigned (v5) ≈ 0.0159。由于prior_assigned(v1)最小,故以v1作为起点进行DFS贪婪划分,v1被划入P1(如图8(a)所示),则划分后剩余节点集合 V={v2,v3,v4,v5,v6,v7,v8,v9,v10,v11,v12,v13,v14,v15,v16,v17,v18,v19,v20,v21,v22,v23},P={P1},P1={v1},area_filled=27,area1= ARPU−area_filled =65−27=38,v6的入度更新为0,v11的入度更新为1。
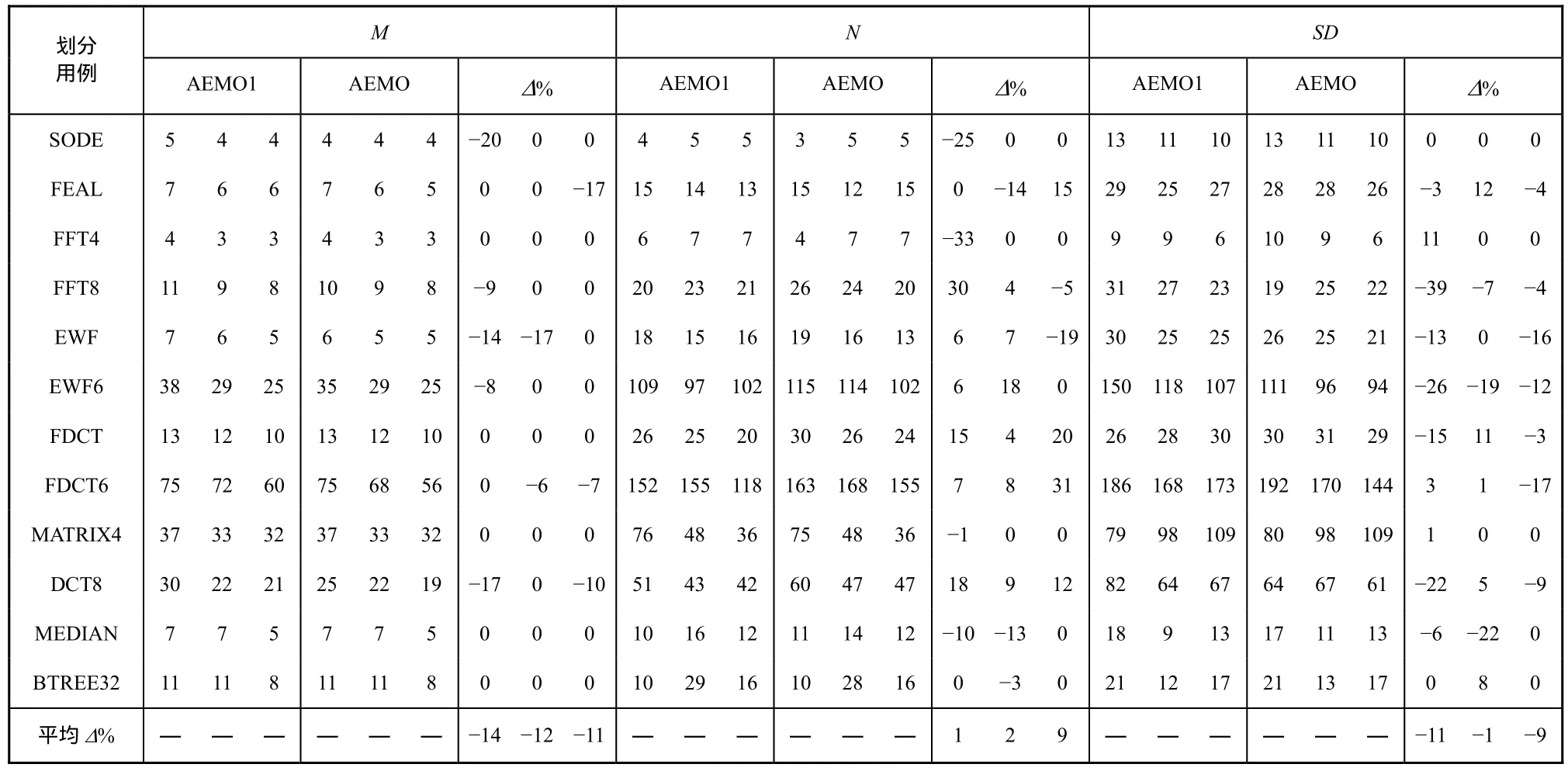
表3 ARPU=56、64、75时AEMO1与AEMO的划分结果
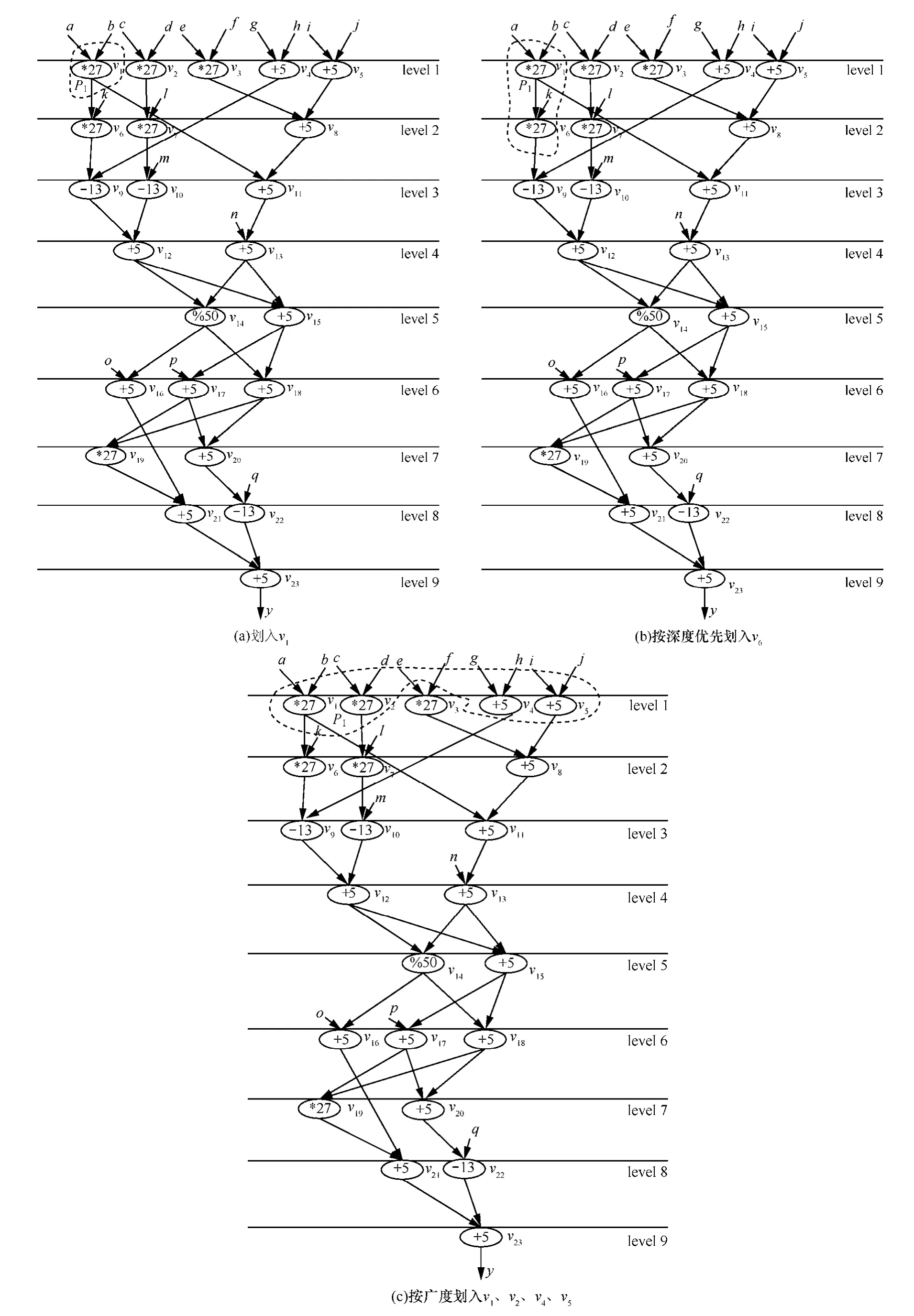
图8 图3(a)算术表达式DFG的第一个划分过程

图9 图3(a)算术表达式DFG的后续划分过程
2) 由于v6为v1的入度已经更新为0的后继,在满足ARPU前提下,按DFS直接预划入(如图8(b)所示),划分后剩余节点集合 V={v2,v3,v4,v5,v7,v8,v9,v10,v11,v12,v13,v14,v15,v16,v17,v18,v19,v20,v21,v22,v23},P={P1},P1={v1,v6},area_filled=54,area1=11,v9的入度更新为1;如果v9和其前驱v4一并划入,则w9+w4=18>area1,由于area1=11大于阈值value,故本次按DFS划分不成功,把划入的节点退回去,相关节点的信息复原。
3) 从v1开始,按权值进行BFS层贪婪划分。由图8(a)可知,就绪节点为v2、v3、v4、v5、v6分别计算其权值prior_assigned(v2)=prior_assigned(v3) ≈ 0.0037,prior_assigned(v4)=prior_assigned(v5)≈0.0159,prior_assigned (v6)=0.0072,由于v2、v3具有相同的优先级,因此按FIFO原则先划入v2,划分后剩余节点集合 V={v3,v4,v5,v6,v7,v8,v9,v10,v11,v12,v13,v14,v15,v16,v17,v18,v19,v20,v21,v22,v23},P={P1},P1={v1,v2},area_filled=54,area1=11,再依次按层贪婪划入 v4、v5,area_filled=64,area1=1,节点调度序列依次为 v1、v2、v4、v5,则 V={v3,v6,v7,v8,v9,v10,v11,v12,v13,v14,v15,v16,v17,v18,v19,v20,v21,v22,v23},P={P1},P1={v1,v2,v4,v5},其划分形状如图8所示。
4) 由图 8(c)可知,就绪节点为 v3、v6、v7、v8,分别计算其权值,prior_assigned (v3)的值小,优先级高,在ARPU约束下,以v3为起点按DFS依次划入v8、v11、v13,因为 area_filled=42,area1=65−42=23>value,故以v3为起点按权值进行BFS层贪婪划分,划分P2节点调度序列依次为 v3、v6、v8、v11,划分后剩余节点集合 V={v7,v9,v10,v12,v13,v14,v15,v16,v17,v18,v19,v20,v21,v22,v23},则 P={P1,P2},P1={v1,v2,v4,v5},P2={ v3,v6,v8,v11},v7、v9、v13的入度更新为0。P2的划分形状如图9(a)所示。
5) 同理,按DFS以优先级最高v7为起点,依次划入v7、v10,因为v12的前驱可以划入,故v9、v12一并划入,而v12、v14不能同时划入,故计算area1=ARPU−(w7+w10+w9+w12)=65−(27+13+13+5)=7<value,更新v13、v14的入度为1,故本次划分按DFS进行,更新就绪点的探测函数值,发现v12可以贪婪划入,综上,划分 P3节点调度序列依次为 v7、v10、v9、v12、v13,划分后剩余节点集合 V={v14,v15,v16,v17,v18,v19,v20,v21,v22,v23},则 P={P1,P2,P3},P1={v1,v2,v4,v5},P2={v3,v6,v8,v11},P3={v7,v10,v9,v12,v13},v14、v15的入度更新为 0。P3的划分形状如图9(b)所示。
6) 同理,按DFS以优先级最高v14为起点,其节点调度序列依次为v14、v16、v15、v18,则P={P1,P2,P3,P4},P1={ v1,v2,v4,v5},P2={ v3,v6,v8,v11},P3={ v7,v10,v9,v12,v13},P4={v14,v16,v15,v18},area_filled=65,area1=0(area1<10),故按DFS执行。需要说明的是,在选取v18和v17时,正在划分的模块与就绪节点之间的边数s起了重要的作用,α=1/9,γ=β=1,level(v17)= level(v18)=6,就绪节点 v17、v18与当前正在划分的模块有向边的数量分别为 1 和 2,outdegree(v17)= outdegree(v18)=2,w17=w18=5,d17= d18=1,prior_assigned(v17) =2/27≈0.0741,prior_assigned(v18) =1/15≈0.0667,故划入 v18,P4的划分形状如图9(c)所示,其中划入v18与划入v17相比划分块间的边数少了一条。
7) 同理,按DFS贪婪划分得到P5如图10所示,其节点调度序列依次为v17、v20、v22、v19、v21、v23,则 P={P1,P2,P3,P4,P5},P1={v1,v2,v4,v5},P2={ v3,v6,v8,v11},P3={ v7,v10,v9,v12,v13},P4={ v14,v15,v18,v16},P5={ v17,v20,v22,v19,v21,v23},V={Φ},划分结束。
5 实验及其分析
本文采用 C语言实现了 ESL、CBP、LSCBP、MOTP、LBP、AEMO 6种时域划分算法,所用的划分基准程序集,统计划分块间输出边的数量方式,ARPU的3种取值,参数α、β、γ的选取等均同4.1节所述。CBP和LBP、LSCBP算法的模块计数均包括第0层输入的划分。下面用AEMO算法分别与LBP、CBP、ELS、MOTP、LSCBP等算法做了比较。
5.1 AEMO算法与LBP算法的比较
用AEMO算法划分图3(a)的DFG的结果如图10所示(ARPU=65),所获得的结果为 M=5、N=11、SD=20,而用LBP算法划分的结果如图11所示,结果为M=7、N=13、SD=17。
因为LBP算法在划分过程中,一遇到不满足硬件资源约束的运算节点就开辟新的划分块,并且把第0层输入作为一个划分块,这些导致了M较大;LBP算法追求每个划分块SD的较小化,但是这将使N较大。AEMO算法消除了LBP算法的缺点,同时对SD进行了折中考虑。其他划分基准对比实验的数据如表4所示,相对于LBP算法,AEMO算法对M和N均有了一定程度的改进,但是SD不如LBP算法。

图10 AEMO划分图3(a)的结果
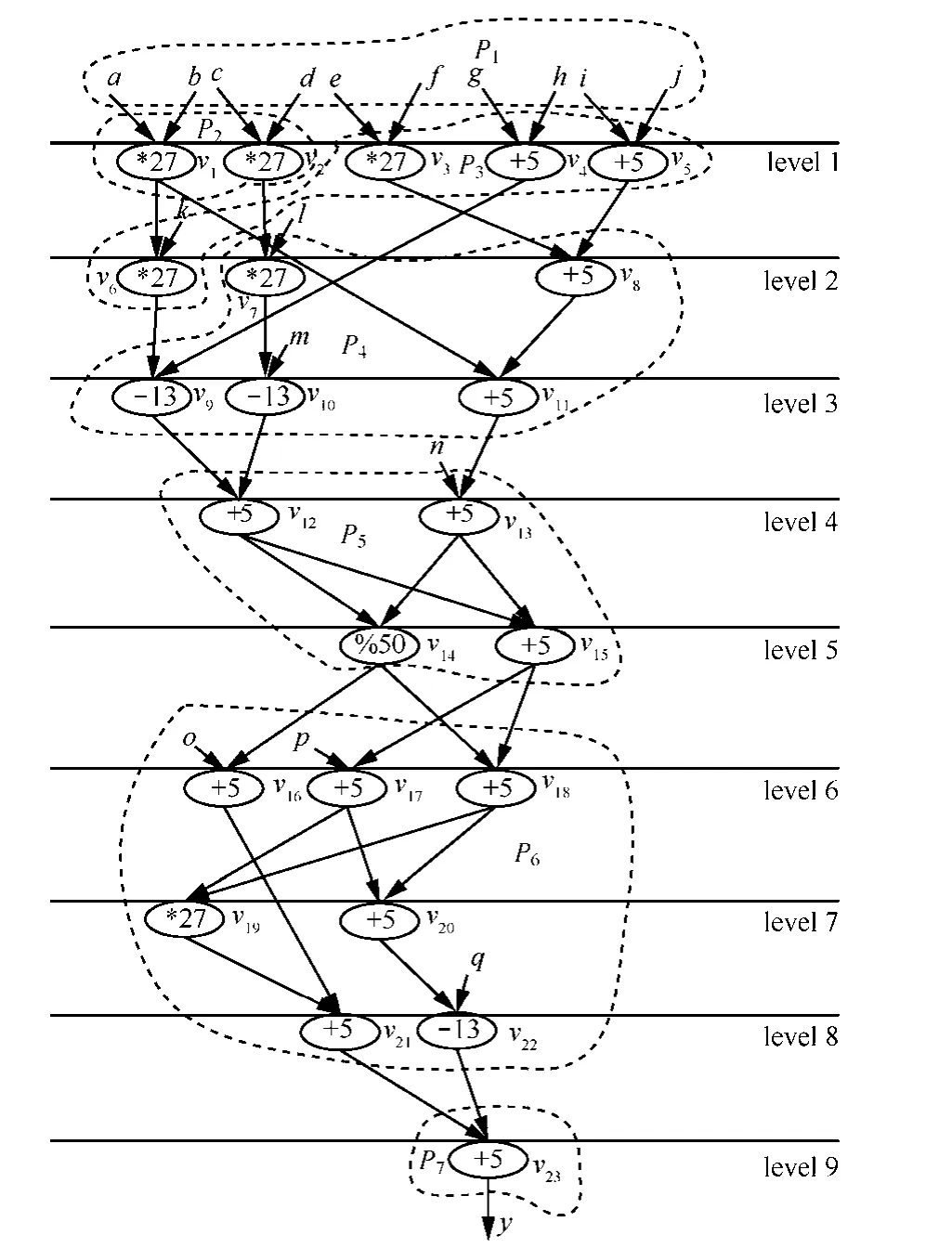
图11 LBP划分图3(a)的结果

表4 ARPU=56、64、75时AEMO算法与LBP算法的划分结果
5.2 AEMO算法与CBP算法的比较
因为 CBP算法尽可能地将联系紧密的运算节点放到一个模块中,但对每个划分块内运算节点的并行度考虑不足,因此N较小,SD较大;M较大的原因同LBP算法。AEMO算法与CBP算法比较的实验数据如表5所示。
5.3 AEMO算法与ESL算法的比较
因为 ESL算法综合考虑了划分块间的通信代价、关键路径等因素,其划分路径多数是沿着深度优先搜索方向延展的,对并行因素考虑不够,而且没有考虑任务 DFG划分中可能产生的硬件碎片问题,因此,相对于 AEMO算法,ESL算法获得较小的N,但是M、SD均较大。AEMO算法与ESL算法比较的实验数据如表6所示。
5.4 AEMO算法与MOTP算法的比较
因为MOTP算法折中考虑了M、SD和N等3个目标,因此获得了较小M,但在每次划分时,没有进行硬件资源面积的估算,这就有可能会产生硬件碎片,所以相比于AEMO算法,M值仍然较大。AEMO算法与MOTP算法比较的实验数据如表7所示。

表5 ARPU=56、64、75时AEMO算法与CBP算法的划分结果

表6 ARPU=56、64、75时AEMO算法与ESL算法的划分结果
5.5 AEMO算法与LSCBP算法的比较
LSCBP算法是对CBP算法的改进,消除了任务DFG划分过程中产生的硬件碎片问题,在追求划分块间的边数较小化的同时,简单考虑了运算任务的并行性,效果较好。但是,LSCBP算法把第0层输入作为一个划分块,且每次划分时没有进行硬件资源面积的估算,因此导致M较大,SD考虑仍然不足,所以相比于AEMO算法,M和SD均较大。AEMO算法与LSCBP算法比较的实验数据如表8所示。

表7 ARPU=56、64、75时AEMO算法与MOTP算法的划分结果

表8 ARPU=56、64、75时AEMO算法与LSCBP算法的划分结果
从上述实验比较结果可以看出,AEMO算法与LBP、ESL、CBP、MOTP、LSCBP等 5种算法相比,AEMO算法获得的M是最小的;除LBP算法之外,AEMO算法的SD均值是最小的,但N值完全优于LBP算法。
采用文献[14]的 10个随机图基准程序,在 ARPU分别为56、64、75的条件下,相比ESL,AEMO算法对 M 改进的相对平均值分别为−5.4%、−6.1%、−8.7%;对N改进的相对平均值分别为+6.7%、+6.8%、+3.0%;对 SD改进的相对平均值分别为−4.6%、−9.3%、−9.3%;相比LSCBP,AEMO算法对M改进的相对平均值分别为−8.2%、−8.7%、−10.7%;对 N改进的相对平均值分别为+4.5%、+4.7%、+3.2%;对SD改进的相对平均值分别为−4.9%、−6.3%、−8.65%。
6 结束语
本文提出了一个 AEMO算法,该算法考察了待划分就绪运算节点的实际情况,实现动态调整节点的调度次序,而且综合考虑了 DFG划分块数和执行总延迟、划分块之间非I/O边数等多个因素,实验结果表明,与LBP、ELS、CBP、MOTP和LSCBP等5种算法相比较,AEMO算法具有最小的M值,即划分模块数少,这意味着配置次数就少,这是影响计算密集型任务关键循环加速的主要因素之一。AEMO算法对N值做了一定程度的优化,比LBP算法少了很多,并且随着 ARPU面积的增大,相比ELS、CBP、MOTP、LSCBP等算法,AEMO算法所获得的SD均值也是最小的,而且它还可以对α、β、γ进行动态调整,以获得单一目标的优化。
[1]CARDOSO J M P, DINII C D, et al.Compiling for reconf i gurable computing:a survey[J].ACM Computing Surveys, 2010, 42(4):1301-1365.
[2]COMPTON K, HAUCK S.Reconfigurable computing:a survey of systems and software[J].ACM Computing Surveys, 2002, 34(2):171-210.
[3]DASU A, PANCHANATHAN S.Reconfigurable media processing[J].Elsevier’s Parallel Computing, Special Issue on Parallel Computing in Image and Video Processing, 2002, 28(7/8):1111-1139.
[4]CAMPI F, TOMA M, LODI A, et al.A VLIW processor with reconfigurable instruction set for embedded applications[J].IEEE Journal of Solid-State Circuits, 2003, 38(11):1876-1886.
[5]王大伟,窦勇,李思昆.核心循环到粗粒度可重构体系结构的流水化映射[J].计算机学报, 2009, 32(6):1089-1099.WANG D W, DOU Y, LI S K.Loop kernel pipelining mapping onto coarse-grained reconfigurable architectures[J].Chinese Journal of Computers, 2009, 32(6):1089-1099.
[6]于苏东,刘雷波,尹首一等.嵌入式粗粒度可重构处理器的软硬件协同设计流程[J].电子学报, 2009, 37(5):1136-1140.YU S D, LIU L B, YIN S Y, et al.Hardware-software co-design flow for embedded coarse-grained reconfigurable processor[J].Acta Electronica Sinica, 2009, 37(5):1136-1140.
[7]DIMITROULAKOS G, GEORGIOPOULOS S, GALANIS M D, et al.Resource aware mapping on coarse grained reconfigurable arrays[J].Microprocessors and Microsystems, 2009, 33(2):91-105.
[8]LEE G, CHOI K, DUTT N D.Mapping multi-domain applications onto coarse-grained reconfigurable architectures[J].IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2011,30(5):637-650.
[9]GPURNA K M, BHATIA D.Temporal partitioning and scheduling data flow graphs for reconfigurable computers[J].IEEE Transactions on Computers, 1999, 48(6):579-590.
[10]周博, 邱卫东, 谌勇辉等.基于簇的层次敏感的可重构系统任务划分算法[J].计算机辅助设计与图形学学报, 2006, 18 (5):667-673.ZHOU B, QIU W D, CHEN Y H , et al.A level sensitive cluster based partitioning algorithms for reconfigurable systems[J].Journal of Computer Aided Design & Computer Graphics, 2006, 18(5):667-673.
[11]JIANG Y C, WANG J F.Temporal partitioning data flow graphs for dynamically reconfigurable computing[J].IEEE Transactions on Very Large Scale Integration Systems, 2007, 15(12):1351-1361.
[12]潘雪增, 孙康, 陆魁军等.动态可重构系统任务时域划分算法[J].浙江大学学报(工学版), 2007, 41(11):1839-1844.PAN X Z, SUN K, LU K J, et al.Temporal task partitioning algorithm for dynamically reconfigurable systems[J].Journal of Zhejiang University (Engineering Science), 2007, 41(11):1839-1844.
[13]CARDOSO J M P, NETO H C.An enhanced static-list scheduling algorithm for temporal partitioning onto RPU[A].Proceedings of 1999 IFIP International Conference on Very Large Scale Integration[C].Lisbon, 1999.485-496.
[14]陈乃金,江建慧,陈昕等.一种考虑执行延迟最小化和资源约束的改进层划分算法[J].电子学报, 2012, 40(5):1055-1066.CHEN N J, JIANG J H, CHEN X, et al.An improved level partitioning algorithm considering minimum execution delay and resource restraints[J].Acta Electronica Sinica, 2012, 40(5):1055-1066.
