基于随机置换展开与停止集的LT码联合编译码算法

焦健，杨志华，顾术实，周洁，张钦宇

（哈尔滨工业大学 深圳研究生院，广东 深圳 518055）

1 引言

近年来，LT码作为一种能够以任意概率逼近香农极限的无码率纠删码，受到分组通信业务的广泛关注[1]。它将带有检错机制的分组交换信道等效为删除信道，将传统纠删编码的处理对象拓展到了数据分组，形成了一种无需反馈链路、高效可靠的前向纠删机制。尤其是码长较短的LT码(103数量级)，适用于节点运算能力受限的容迟网络场景的信息纠错(如物联网、深空探测等)。LT码的编译码算法的渐近性能取决于输出度分布的选择[2,3]，度的平均值是衡量编码冗余与编译码复杂度的关键参数，目前采用的经典输出度分布是鲁棒孤波分布及其优化解。Luby设计了一种低复杂度的消息传递(BP,belief propagation)译码算法，译码的复杂度与编码Tanner图的关联边数成正比，当输入节点数量较大时，BP译码算法对符合泊松分布输入度分布的译码性能最优[4,5]。但是，LT码的随机编码方式以及生成矩阵的稀疏特性，使其在码长较短时无法保证对输入节点的全选覆盖，需要较大的编码冗余才能保证恢复所有的输入节点。

针对这个问题，通过引入修正的期望可译集(ERS)可得到短码长LT码的离散密度进化度分布[6]，但该分布只能保证恢复出尽量多的原始数据分组，而不是恢复出整个原始文件。Hyytia引入马尔科夫过程进行建模，通过较高复杂度的算法设计，给出了极短码长条件下(小于 100)LT码的最优解[7]。Zhu提出了一种度分布优化算法[8]，该算法给出了中短码长的次优LT码度分布。而Huang等人利用混沌算法和Logistic映射改进短码长LT码的编码算法，在编码冗余较大时(0.37～0.45)获得了性能优化[9,10]。Gong提出了LT码的Tanner图展开PEG(progressive edge-growth)算法[11]，尽可能选择具有最小度数的未被覆盖的信息节点与输出节点相连，并试图获得输入节点的泊松分布，该算法对于构造实用短码长的LT码提供了有益的探索。在LT码译码研究方面，许多研究把 Turbo、LDPC码的似然译码技术引入到喷泉码的译码算法中，以解决BP译码算法效率不高的问题。Sarwate提出了类似最大似然的译码算法[12]，充分利用信道状态信息等软信息设计了似然译码算法。Heo提出了一些改进算法降低了译码复杂度[13]，但实现起来较为困难。Kim提出了Raptor码的渐增高斯译码算法[14]，通过设计类似高斯译码矩阵求逆的方式进行译码，获得译码性能与译码算法复杂度较好的折衷，为喷泉码的改进提供了一种可借鉴的思路。以上分析表明，随机编码方式使得短码长LT码需要较高的编码冗余才能保证接收端能够恢复所有的原始信息。而目前普遍采用的BP译码算法启动门限较高，需要收到绝大部分的编码分组才能进入译码瀑布区。本文综合考虑上述短码长LT码的优化设计问题，提出了基于随机置换展开与停止集的联合编译码算法，限制编码过程中节点的随机连接性，充分利用 BP译码过程的剩余信息，有效地提高了短码长 LT码的编译码性能。

本文第2节针对编码Tanner图，设计了针对短码长LT码的随机置换展开(RPEG, random permute edge-growth)算法，给出了算法的可译码概率与所需的编码冗余理论表达式。第3节针对BP译码算法效率不高的问题，设计了停止集高斯译码(SSGE,stopping set gaussian elimination)算法。第4节针对所设计的联合编译码算法进行了仿真分析和结果讨论。最后给出了本文的结论。

2 基于随机置换展开的编码算法

给定 LT码的输入分组数据向量 S: S={S1,S2,… ,Sk}，输出数据向量D:D ={ D1, D2,… ,Dn,…}和输出度分布生成函数Ω(x):Ω(x) =，Ωi为重量为 i的输出分组在全体输出中的归一化比例，则LT码的编码过程可表示为

其中，G为表征编码关系的k×n阶生成矩阵。根据式(1)及矩阵理论可知，当且仅当矩阵 G行满秩，接收端才可能译码成功，即输入节点全选是其必要条件。

定义随机编码方式的LT码参数(k, n, Ω)，输入节点个数为k，输出编码分组数为n，以概率Ωi产生一个重量为i的输出分组(即Tanner图中与该输出分组连接的边数量为i)，则一个输出分组的平均关联边数量为=Ω'(1)，因此 Tanner图共有nΩ' (1)条连接边。而一个特定输入节点在一次随机编码过程中未被选中的概率为(1- 1 k)，则影响LT码可译码性能的输入节点漏选概率 P可由下式计算

以具有稀疏特性的鲁棒孤波分布(RSD, robust soliton distribution)为例，设不可译概率参数δ，译码算法可靠性参数 c，定义R =(k δ)，则度分布生成函数Ω(x)为[15]

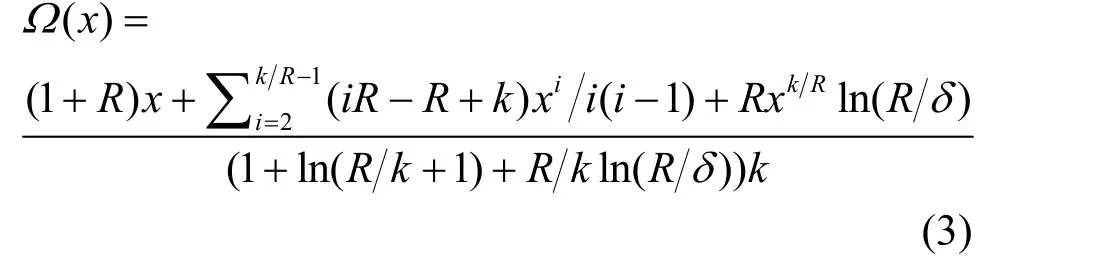
将式(3)代入式(2)可计算出保证 LT码可译码概率达到 10−4时，编码端的输入节点数量与对应的最少编码分组个数，表1给出了码长为1000以下的计算结果(取c=0.03，δ=0.05)。由表1可以看出，对于103及更小码长的LT码，使用随机编码方式的LT码不可避免地需要增加编码冗余以保证译码可靠性。

表1 鲁棒孤波度分布译码失败概率10−4所需编码分组数量

针对此问题，本文提出基于随机置换展开(RPEG)编码算法，该算法通过限制LT码随机编码方式的随机性，提高码字距离，以较小的编码冗余达到输入节点的全选覆盖。设 RSD度分布的重量为Ωw，定义LT编码分组Di,j，其中，i≤N表示编码分组的数量，j表示第j个RPEG的置换展开区间；{Di,j}表示 Di,j中包含的原始分组；在第 j个RPEG置换展开区间的编码向量选择空间为Sj，且累计的原始编码分组个数为Wj，具体算法流程如图1所示。

Tanner图如图2所示，由算法步骤及图2(a)可知，Tanner图的输入节点是近似于均匀分布的，而输出节点度分布仍维持所选取的鲁棒孤波分布，RPEG算法在没有改变度分布和编码复杂度的前提下，提高了码字距离，保证了编码分组对原始信息的随机均匀覆盖，图2(b)直观地体现了其优化效果。Tanner图中小环的存在严重影响LT码的译码性能，本文提出的RPEG编码算法尽力抑制编码过程中小环的产生。但在抑制小环的同时，需要注重保留码字之间的一定相关性，避免BP译码过程提前终止，以保证对完全无环的Tanner图的译码可靠性。

通过小环产生概率的推导给出对此问题的分析。给定随机编码方式的LT码参数(k, n, Ω)，则k×n阶编码生成矩阵G中度为i的列向量生成概率为

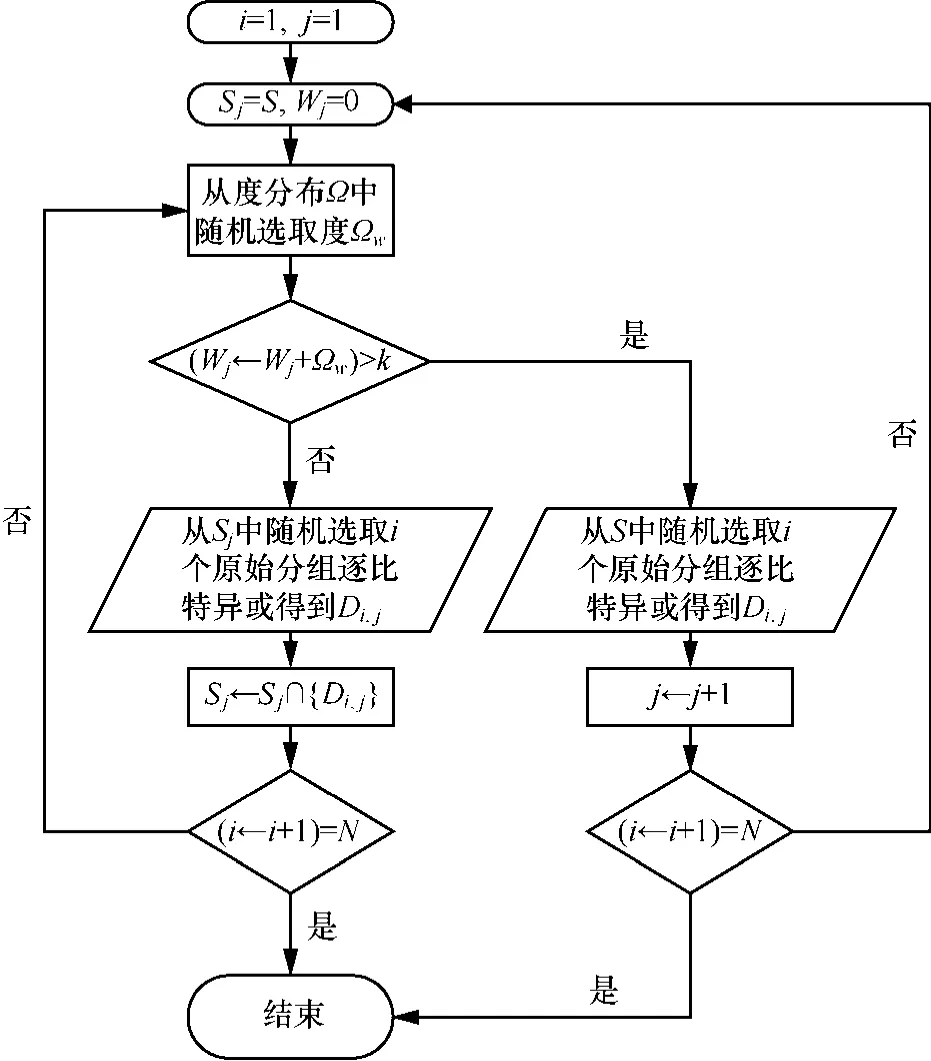
图1 随机置换展开编码算法流程

而生成矩阵G中存在环长为4即存在另一列与该列在2个相同的行位置为1，设该列的度为j，显然有i, j＞1，则这两列具有4环的概率Pgirth4(i,j)为

图2 随机置换展开编码算法的Tanner图

则对于k×n阶编码生成矩阵G存在4环的概率Pgirth4为

由RPEG编码算法可知，构造的k×n阶编码生成矩阵GRPEG近似地分为nΩ'(1)k个随机置换展开区间，通过设置可在同区间内完全避免4环的产生。设α=k Ω'(1)，根据式(6)可近似地推导出RPEG编码的4环生成概率Pgirth4_RPEG为

由式(7)可以看出，控制参数α可以实现性能改进，即通过降低输出节点的平均度'(1)Ω来降低环的生成概率，并且不会对式(2)计算漏选概率产生影响。以编码复杂度为常数的弱鲁棒分布(WRSD)为例，其生成函数为[3]

3 面向随机置换展开编码算法的BP译码算法改进

针对随机置换展开编码的LT码，本文采用具有较低计算复杂度的BP译码算法进行译码。如果想要保证BP算法的译码过程顺利进行，必须满足每一步译码之后译出新的度为 1的分组，否则 BP译码中止。因此，译码过程中每一步的失败概率是衡量BP译码算法的重要性能指标。

定义1 LT码的BP译码状态为(u, r, c)，u为此刻未译码的输入节点数量(u≤k)，r为该时刻BP译码传递波纹算子(即译码缓存中度为 1的包)，c为该状态下缓存中度大于1的分组。则译码器对于一个度为i的输出分组Di进行译码，在该译码状态下能够成功恢复出一个新的输入节点的概率p(i, u)为[2]

在式(9)中，度为i的编码分组Di所连接的输入节点包括:1) 1个输入节点，是第(k−u)次BP译码中即将译出的输入节点；2) 1个输入节点，包含在u个未译码的输入节点集中；3) (i−2)个输入节点，包含在已被译码的(k−u−1)个输入节点集中。结合LT码的度分布Ω，可获得此状态下译码器能够译出一个新的输入节点的概率。

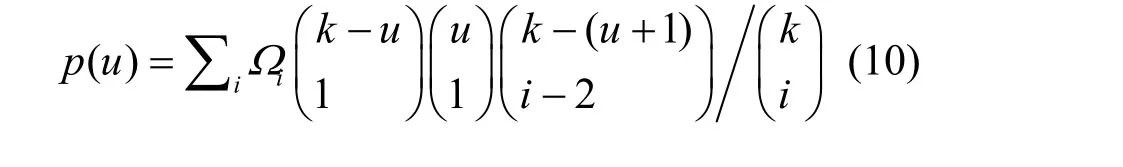
式(10)仅包含了此状态下被译码的编码分组，其所连接的输入节点的一种组成情况。

对于度为i的编码分组Di所连接的另外一种输入节点组成:1) 1个输入节点，在第(k−u)次BP译码时即将被译出的输入节点；2) (i−1)个输入节点，包含在已被译码的(k−u)个输入节点集中，概率为

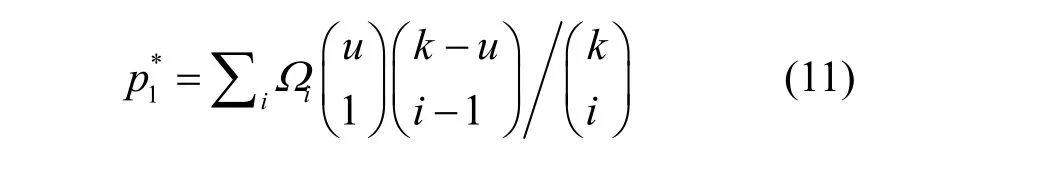
同时，还存在着编码分组Di所连接的第3种输入节点组成，即该编码分组中所有的输入节点都已经在第(k−u)次BP译码之前被译出的情况

联立式(10)～式(12)即可获得 BP译码的状态转移概率pu[15]

给定译码器的状态转移概率pu，可以推出译码器各个状态转移到BP译码停止状态(u＞0, r=0, c＞0)的概率，此概率即为BP译码在每一步译码过程中可能的失败概率。

针对BP译码过程的提前中止问题，本文充分利用BP译码过程中的剩余信息，采用高斯消去(GE,gaussian elimination)译码算法重新启动译码过程，保证译码的顺利完成，该算法既解决了BP译码停止问题，也降低了全局采用GE译码的译码复杂度。

图3 RSD分布随机编码的BP停止集

图4 RSD分布RPEG编码的BP停止集

图5 WRSD分布RPEG编码的BP停止集

定义2 给定编码冗余下，BP译码提前终止时剩余的所有度大于1的编码节点集合称之为停止集H。图3～图5给出了原始分组数量分别100, 300, 500,800, 1000条件下，运行10000次BP译码(迭代20次)在不同编码冗余下的归一化停止集大小。可以看出，1000以下的短码长LT码运用BP译码算法，译码停止集在编码冗余接近0.25之后才逐渐消失，在编码冗余为0.1～0.2区间里，归一化的停止集接近0.2左右，采用停止集高斯译码算法(SSGE)，存在很大的可利用空间。

基于BP译码的停止集，下面给出具体的算法模型，设接收端正确收到的编码分组构成的生成矩阵为G，则流程如图6所示。

图6 停止集高斯译码算法流程

相对于采用全局高斯译码算法，本算法的译码开销与前半段BP译码过程能恢复的原始节点数量有关。由图3可知，随着BP译码能恢复绝大部分的原始节点，译码失败时G中剩余的停止集H较小，所带来后续高斯译码的译码开销相对较小。若归一化停止集比例设为η，对于采用 RSD分布编码的SSGE译码开销为O( nlog(k)+(η k)3)，而采用WRSD分布的 SSGE译码开销为O( n log(+(ηk)3)，对于特定的编码冗余(如0.25)，则增加的译码复杂度几乎可忽略。

4 仿真结果讨论

本文中把译码失败次数占总仿真次数的比例，即译码失败概率(decoding failure rate)作为衡量LT码性能的重要指标，通过仿真对比分析提出的RPEG编码算法，SSGE译码算法以及采用联合编译码算法的性能，表2给出仿真参数配置。

表2 蒙特卡洛仿真参数配置

4.1 RPEG编码方案对于BP译码算法可译码性能的改善

图7给出了RPEG编码方式下RSD和WRSD 2种度分布在原始数据数量为 k=100, 300, 500,800, 1000时，随着编码冗余变化所对应的译码失败概率曲线。结果表明，码长为1000和800的LT码采用RPEG编码算法后，以增加一个可选输入节点缓存空间的代价，只需0.3的编码冗余即可达到10−4的译码失败概率。与表1中所需编码冗余比较，明显提高了103及以下码长的BP译码性能。因此，RPEG编码方案可以充分保证输出编码数据的可解性，对于编译码缓存空间受限和实时性要求较高的可靠传输业务具有广泛的应用前景。

RSD的编码开销为O(nlog(k))，WRSD的编码开销为O(nlog(1/ε))，表3进一步给出了对应码长的RSD与WRSD的平均度，其中，WRSD的平均度由参数ε唯一确定，而RSD的平均度随着输入节点 k的增加以log(k)增加。而图7(a)的WRSD与图5(b)RSD的BP译码性能非常接近，甚至在某些编码冗余点上较 RSD的译码性能稍好，验证了式(7)描述:通过降低LT编码分组的平均度，能增大RPEG编码过程中置换展开的空间，从而降低小环产生的机率，获得BP译码性能的提升。

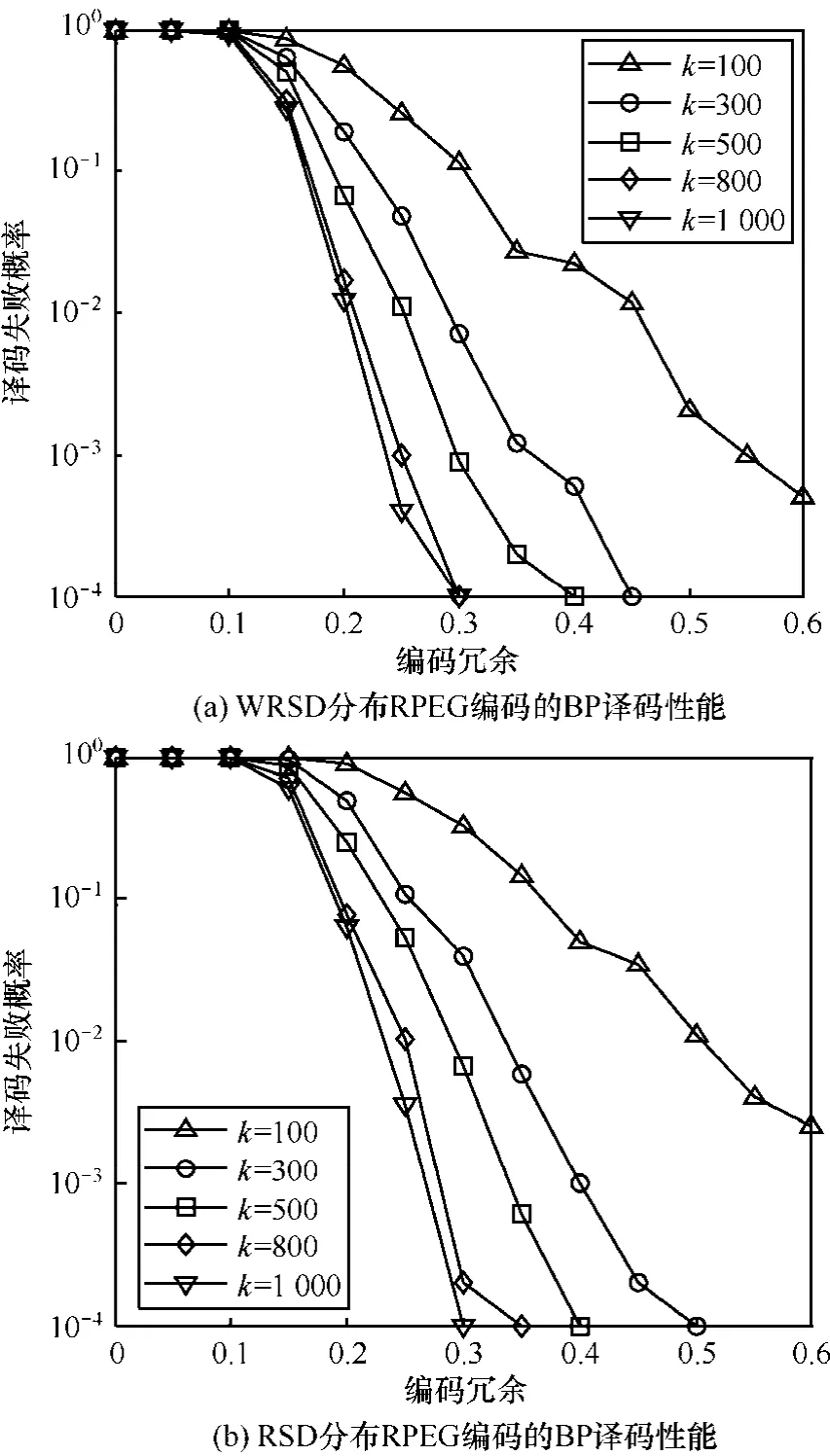
图7 RPEG编码的BP译码性能

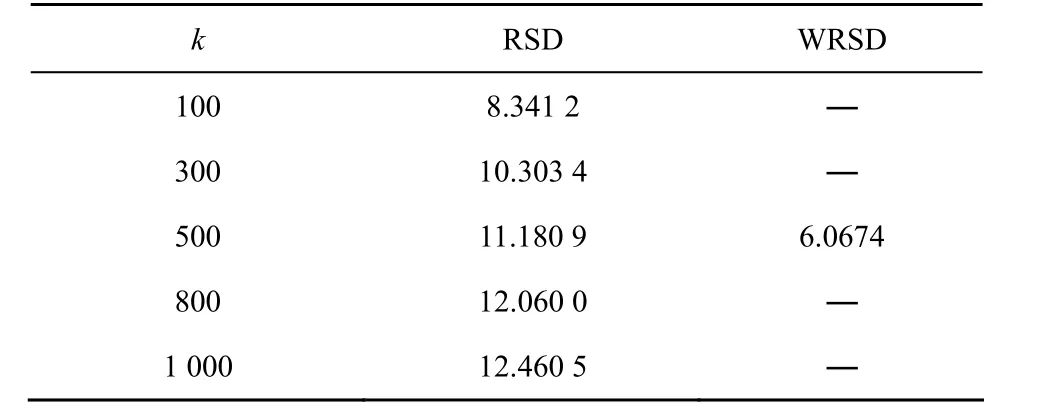
表3 RSD与WRSD不同码长的平均度

4.2 RPEG编码算法在不同信道条件下的译码性能

给定发送端输出n=2k数量的LT编码分组，以随机删除信道的分组丢失率作为信道参数，接收端能接收的分组数量从 k增加到 1.6k，图 8给出了RPEG编码的LT码在不同信道参数条件下(分组丢失率变化)的译码性能。可以看出，在信道逐渐变差时，RPEG算法的编码输出分组仍然能保持LT码接收到一定数量编码分组后，以较高的概率恢复全部原始信息。这是RPEG编码算法与类LDPC编码结构或PEG技术相比，其优势所在。后2种类似固定编码结构的算法在高分组丢失率的环境下，无法应付信道中的突发差错，译码性能急剧下降。而RPEG编码算法具有随机编码特点，在面临信道条件变差时性能上更趋稳定[16,17]。进一步对比图8(a)与图 8(b)可发现，WRSD在分组丢失率大于0.25时，已无法达到10−4的译码失败概率，而相同条件下 RSD可对抗 0.325左右的分组丢失率。这是由于RSD的平均度较高，比WRSD分布通过RPEG编码置换展开的区间更多，因此发生分组丢失时，仍有相当数量的展开区间维持完整以保护译码性能的顽健性。

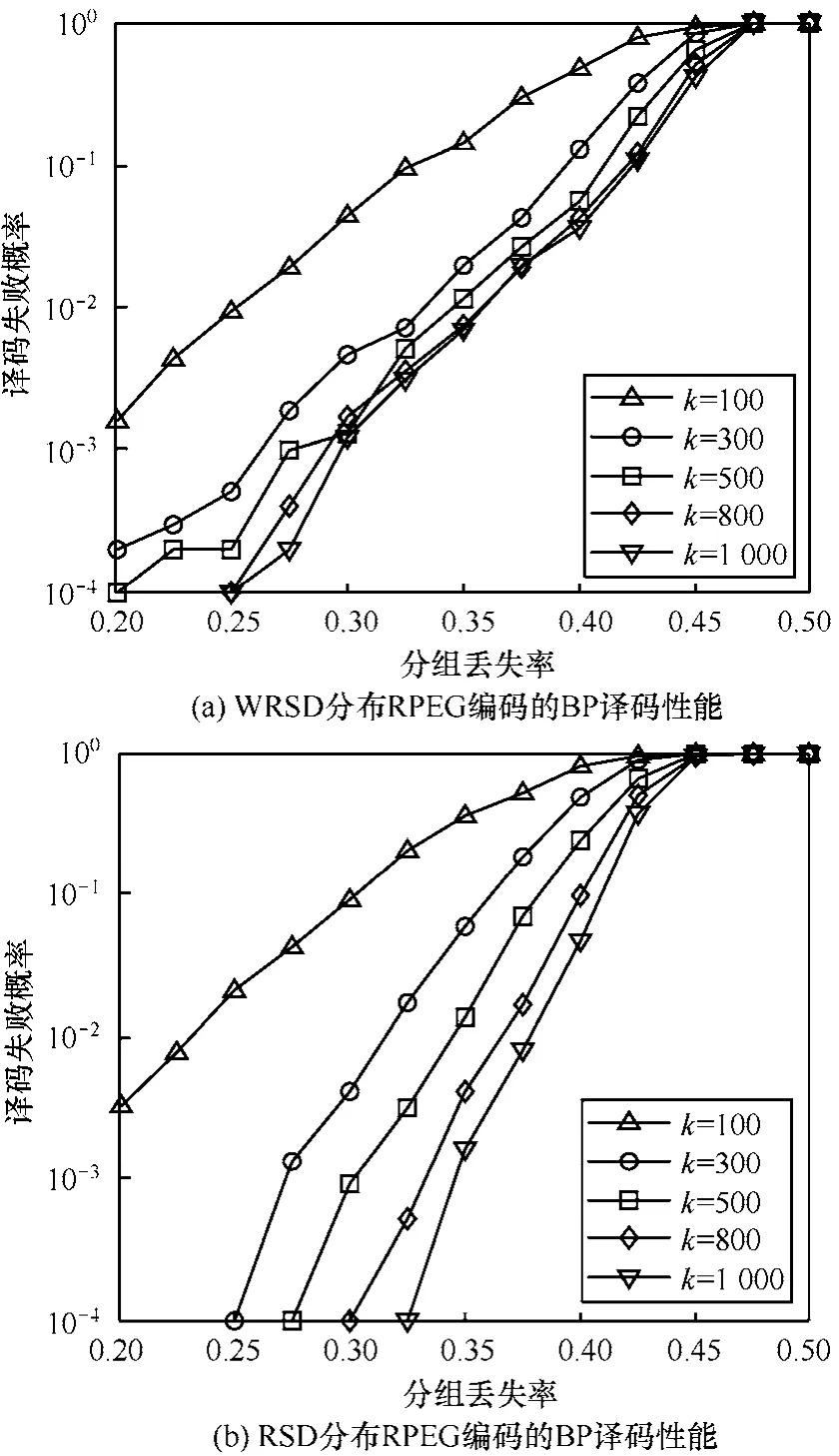
图8 随分组丢失率变化的RPEG编码BP译码性能

4.3 随机编码方式下SSGE译码算法的性能比较

图7对比了在码长k≤1000的LT码采用RSD随机编码方案下，不同译码算法的译码失败概率。从图9(a)可以看出，BP译码算法需要0.5以上的编码冗余，才能达到10−4的译码失败概率。随着码长降低，所需的冗余进一步加大。而图9(b)的GE译码算法，在相同的编码冗余下能达到稍低的译码失败概率，相比于BP算法更接近可译码极限。图9(c)的SSGE译码性能曲线与图9(b)几乎一致，证明第3节给出的SSGE算法在BP译码算法的基础上通过增加有限的译码复杂度，使得LT码的译码性能逼近最大似然译码的性能。

图9 RSD分布随机编码的BP、GE、SSGE的译码性能比较

4.4 RPEG编码算法与 SSGE译码算法的联合编译码性能

在以上实验的基础上，联合采用RPEG编码算法与SSGE译码算法，分析其对短码长LT码性能的改善作用。图10给出了短码长LT码采用RPEG编码与SSGE译码算法后的译码失败概率。对比图10与图7、图9可以看出，联合编译码算法在没有改变度分布的前提下，通过对Tanner图连接边过程的随机性进行部分限制，提高了码字距离，获得对原始信息的随机均匀覆盖，提高了短码长下生成矩阵G的行满秩概率。联合算法随着输入节点的增加迅速地提高了LT码的译码性能，对于800和1000的码长只需要不超过0.1的编码冗余，就能达到10−4的译码成功概率。而对于500和300码长也降低了20%的编码冗余开销，算法的计算复杂度与直接使用GE相比降为O(η3)。

图10 RPEG编码与SSGE译码的联合算法

5 结束语

针对短码长(103以下)LT码设计中，在保证较稳定的译码恢复概率时，需要增加编码冗余的问题，本文设计了RPEG算法以限制编码矩阵Tanner图连接边的部分随机性，使得输入节点变为近似均匀的度分布，提高了码长为103以下短码长喷泉码的可译码性能。在此基础上，充分利用了BP译码算法的剩余信息，设计了基于停止集的SSGE译码算法，实现了在接收编码冗余0.2以上的条件下，以约等于GE译码开销O(η3)的计算复杂度获得最大似然的译码性能。仿真结果表明，在保留LT码无码率特点的情况下，采用上述联合编译码算法，相对于传统的 LT码编译码算法具有较大的性能优势，实现了短码长LT码设计中编码冗余与译码性能之间的折衷。未来将从理论分析角度深入研究LT码字中小环与BP译码的关系，以探明LT码BP可译的充分条件，并进一步提高RPEG算法编码性能。

[1]慕建君,焦晓鹏,曹训志.数字喷泉码及其应用的研究进展与展望[J].电子学报, 2009, 37(7):1571-1577.MU J J, JIAO X P, CAO X Z.A survey of digital fountain code s and its application[J].ACTA Electronica Sinica, 2009, 37(7):1571-1577.

[2]LUBY M.LT codes[A].43rd Annual IEEE Symposium on Foundations of Computer Science[C].Vancouver, BC, Canada, 2002.271-282.

[3]SHOKROLLAHI A.Raptor codes[J].IEEE Transactions on Information Theory, 2006, 52(6):2251-2567.

[4]MACKAY D J.Fountain codes[J].Proceedings of IEEE Communication.2005, 152(6):1062-1068.

[5]SHOKROLLAHI A.New sequences of linear time erasure codes approaching the channel capacity[A].Proceedings of 13th Conference on Applied Algebra, Error Correcting Codes, and Cryptography[C].Springer Verlag,1999.65-76.

[6]ZHU H J, ZHANG C, LU J H.Designing of fountain codes with short code-length[A].IWSDA 2007[C].2007.65-68.

[7]HYYTIA E, TIRRONEN T, VIRTANO J.Optimal degree distribution for LT codes with small message length[A].Infocom 2007[C].2007.2576-2580.

[8]朱宏鹏,张更新,李广侠.卫星数据广播分发系统中的LT的研究[J].通信学报.2010, 31(7):122-128.ZHU H P, ZHANG G X, LI G X.Research of LT code in satellite data broadcasting system[J].Journal on Communications, 2010, 31(7):122-128.

[9]黄诚,易本顺.基于抛物线映射的混沌LT编码算法[J].电子与信息学报.2009, 31(10):2527-2530.HUANG C, YI B S.Chaotic LT encoding algorithm based on parabolic map[J].Journal of Electronics & Information Technology, 2009,31(10):2527-2530.

[10]黄诚,易本顺.喷泉码的 Logistic映射实现[J].北京邮电大学学报,2009, 32 (1):103-106.HUANG C, YI B S.Implementation of fountain codes using Logistic map[J].Journal of Beijing University of Post and Telecommunications,2009, 32 (1):103-106.

[11]龚茂康.中短长度 LT码的展开图构造方法[J].电子与信息学报.2009, 31(4):885-888.GONG M K.Unfolding graphs for constructing of short and moderate-length LT codes[J].Journal of Electronics and Information Technology, 2009, 31(4):885-888.

[12]SARWATE A.Rateless coding with partial CSI at the decoder[A].IEEE Information Theory Workshop[C].2008.378-383.

[13]HEO J, KIM S.Low complexity decoding for raptor codes for hybrid-ARQ systems[J].IEEE Transactions on Consumer Electronics,2008, 54(2):390-395.

[14]KIM S, KO C.Incremental gaussian elimination decoding of raptor codes over BEC[J].IEEE Communication Letters, 2008, 12(4):307-309.

[15]MAATYOUK E, SHOKROLLAHI A.Analysis of the second moment of the LT decoder[A].ISIT2009[C].Seoul, Korea, 2009.2326-2330.

[16]林广荣,林新荣,依娜等.基于 LDPC码的数字喷泉编码[J].电子与信息学报.2008, 30(4):822-825.LIN G R, LIN X R, YI N, et al.Digital fountain base on LDPC code[J].Journal of Electronics and Information Technology, 2008,30(4):822-825.

[17]林广荣,依娜,董明科等.基于停止集的喷泉编码有限长性能估计[J].电子与信息学报, 2008, 30(11):2634-2637.LIN G R, YI N, DONG M K, et al.Finite length analysis of fountain codes based on stopping set[J].Journal of Electronics and Information Technology, 2008, 30(11):2634-2637.