问题驱动下的一节复习课
——基本不等式的章节复习课实录及反思
2013-10-26
●
(龙泉市中等职业学校 浙江龙泉 323700)
问题驱动下的一节复习课
——基本不等式的章节复习课实录及反思
●邹必珍
(龙泉市中等职业学校 浙江龙泉 323700)
章节复习课的常见套路是:知识梳理——例题讲评——方法提炼——习题训练,其优点是:教师可以掌控课堂,容量大,节奏快;其缺点是:对学生限制过多,学习被动,有效性不高.为探讨如何提高章节复习课的有效性,浙江省龙泉市在数学名师的组织与指导下,采取校际合作、课例研讨的形式,围绕“问题驱动下的章节复习课”这个主题进行了听课、评课、改进等一系列的研讨活动,其中不乏精彩的案例,现择其一例,赘述如下,以求教大家.
1 课堂实录
1.1 问题启动,梳理知识,提炼方法
师:请同学们思考:已知x>0,y>0,且2x+8y-xy=0,求xy的最小值.
生1(演板):由2x+8y-xy=0可得


师:你是如何想到的?
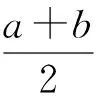
师:回答得很好,抓住了运用基本不等式解题的结构特征:和积形式上的转化.但上式中的最小值能取到吗,此时x,y的值是多少?
生2:当x=16,y=4时取到最小值.
师:在运用基本不等式求最值时一定要考虑等号是否成立.
1.2 学生编题,激活思维,拓展能力
师:下面给大家几分钟的时间,在不改变题目条件的情形下,编出新题,并尝试去解决这些问题.
(学生思考与编题.)
师:下面请大家说说自己编出的题及编题的思路.
生3:我编出的题目是“求x+y的最小值”,我想xy有最小值,x+y可能就在积最小时取到最小值20.
生4:我编出的题目是求“xy的最大值”,既然在限制条件下有最小值,我猜想可能也会有最大值.
生5:我编出的题目是“求x+y的最大值”,我是把积式改为和式,最小值改为最大值.
生6:我编出的题目是“求x+4y的最小值”,因为和式提出2之后就是x+4y,而积式通过配凑系数可以凑成(x+4y)2的形式,我可以上来写吗?
师:当然可以啊!
生6(演板):由已知可得
从而
x+4y≥32,
因此当x=16,y=4时,x+4y取得最小值32.
师:想法真好,能够抓住系数特征,对积的系数进行配凑,并运用基本不等式改编出新题,化积式为和式,写得也很完整.
(笔者敏锐地意识到xy,x+y的最大值不存在,如何处理不存在问题可能比单纯处理最值存在的问题更有价值.)
师:大家用类比、联想、配凑的方法,编出了很多新题,真的很有想法,不错!这些问题都可以求解吗?怎么求解呢?若不能求解,请说明理由.大家不妨动手试试.
生7(演板):由条件可得

从而
x+y-10≥8,
即
x+y≥18,
因此当x=12,y=6时,x+y的最小值为18.
师:能说说你是怎么想到的吗?
生7:要求x+y的最小值,条件中的积式可以化成x+y的形式,但和式不能化成x+y形式,我想不能直接用基本不等式了,先把整个条件写成2个分别只含有x,y的一次式的乘积,尝试后发现可以写成……
师:哦,想法真不错!大家看看有什么需要补充的吗?
生8:开方的时候为什么只取x+y-10≥8而舍去了x+y-10≤-8.由x+y-10≤-8可得x+y≤2,岂不是x+y的最大值为2?
生9:这不可能,最大值怎么可能比最小值小呢?
师:那问题出在哪儿?
生10(演板):我这样解,可以避免这个问题出现:由2x+8y-xy=0可得


……
师:你是怎么想到这样求解的呢?
师:要是把问题改为:求x+3y的最小值呢?


师:方法1的关键是利用常数1,方法2的关键是配凑系数.虽然问题解决了,但是前面的开方为什么不能取负值的问题还没有解决,大家有什么想法吗?
1.3 释疑解惑,揭示本质,贯通联系
生13:题目条件可以变为2x=y(x-8),因为x>0,y>0,所以x>8,故x+y≤2不可能成立.
师:这只是解释了x+y≤2不成立,在解题过程中我们应该怎么叙述,哪位同学可以补充完整?
(学生叙述解题过程.)
师:小小等式左右移,移法不同乾坤大.2x=y(x-8)还能变吗?
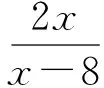
师:如果说前面几位同学对条件的转化是“量变”,你刚才这一小步就促成了“质变”,把等式问题转化成了函数问题,这是什么函数呢?
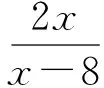
(学生主动要求上来画图.)
师:图像出来了,大家有什么启发?
全体学生:xy,x+y不可能有最大值.
师:同学们,出一道题不容易,类比、联想得到的一些结论不可靠.解决一个问题也不容易,但是要说明一个问题不可解则需要更大的智慧和勇气.
1.4 归纳方法,体悟思想,强基固本
师:请思考下列问题,从知识、方法、易错点等层面梳理本节课的学习.
(1)基本不等式的核心知识是什么?基本方法是什么?
(2)运用基本不等式解题的易错点在哪里?
学生回答,教师边补充、边板书,完成从知识到方法、从单一的知识点到知识网络的构建.
2 课后思考
章节复习课是常见的课型之一,是新课结束之后对章节核心知识的梳理、基本方法的提炼与落实、前后知识的融会贯通.本节课试图通过一个问题及其深化达成这个目的.
2.1 在追问中梳理核心知识,提炼方法
2.2 在释疑解惑中贯通知识间的联系,提升能力
学生具有较强的类比、联想能力,在编题环节,学生通过类比、联想编出了“求xy的最大值”和“求x+y的最大值”这2个没有确定解的问题,教师没有直接告诉学生这2个问题没有解,而是敏锐地捕捉时机围绕“开方之后为什么只取正值?”展开讨论,在学生给出正确解法后还继续追问“合理解释”,催生出了最后的质变“把等式转化成函数”,在函数观点下再审视问题,学生心中的疑问豁然开朗,既解释了为什么不能求解,又实现了函数与(不)等式(方程)之间的转换,让学生在潜移默化中体验这种转化,提升能力.
2.3 在解题过程中引导学生用数学语言表达
“不仅要学会用数学方式思考,还要学会用数学方式表达”,科学、精炼的表达是解题的基本要求.学生1尽管求出了结果,但忽视了等号成立的条件,一句“最小值能取到吗?”让学生感受到了能否取到等号的重要性;学生8在开方时取正去负,虽然其他学生为其补充了理由,教师依然要求学生口述解题过程,对解题过程完整性的要求可见一斑.对问题“求xy的最大值”和“求x+y的最大值”的探究,其本质就是给学生示范怎么去表达数学问题,如何正确表达过程,不能求解如何说明理由.
[1] 施仁智,江建国.让学生在自然的思考过程中催生新想法[J].中学教研(数学),2012(3):21-23.
[2] 柳小平,郭楚明.角色转换 深化理解 感悟本质 有效建构——高三第一轮复习“求点的轨迹方程”教学简录及反思 [J].中学数学,2011(7):59-61.
