一道新定义几何题的“前生、今世、未来”
2013-10-26
●
(台州市教育局教学研究室 浙江台州 318000)
一道新定义几何题的“前生、今世、未来”
●蒋荣清
(台州市教育局教学研究室 浙江台州 318000)
碰到一道好的数学题,看过、做过、反思过之后,犹如品茶的3种境界——得到、得韵、得味.近几年在初中毕业生学业考试中,新定义的试题屡见不鲜,这些题往往让人眼前一亮,颇具匠心.2011年台州市初中毕业生学业考试中一道新定义的几何题,给笔者留下了深刻的印象.

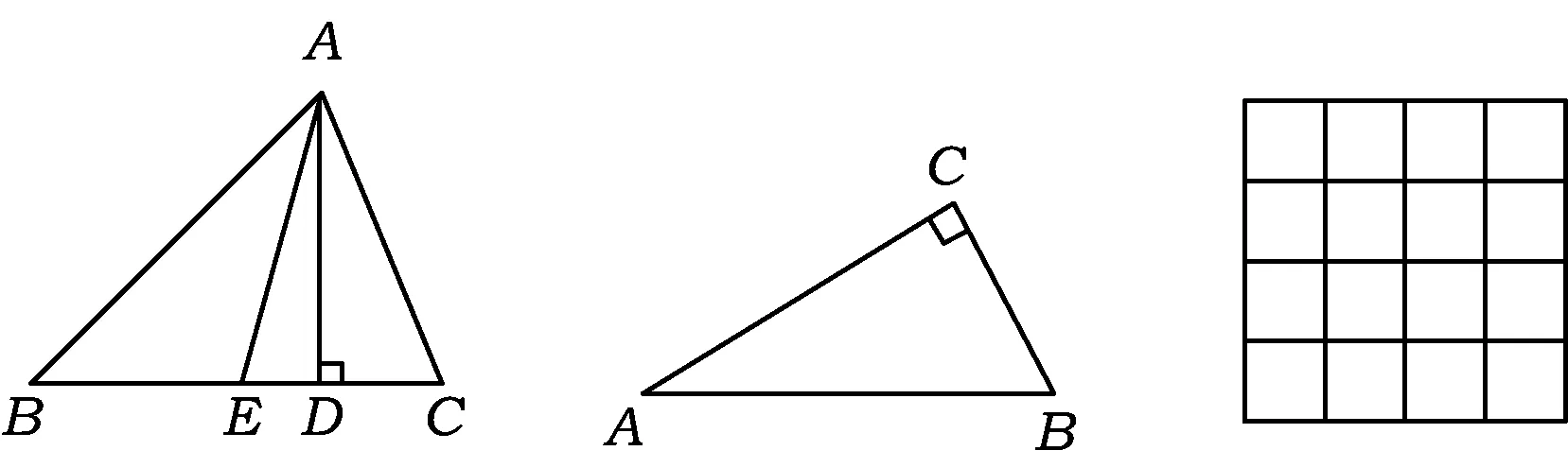
图1 图2 图3
(1)如图2,已知在Rt△ABC中,∠A=30°,求λA,λB.
(2)在每个小正方形边长均为1的4×4方格纸上(如图3),画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且λA=2,面积为2.
(3)判断下列3个命题的真假(真命题打“√”,假命题打“×”):
①若△ABC中λA<1,则△ABC为锐角三角形;
( )
②若△ABC中λA=1,则△ABC为直角三角形;
( )
③若△ABC中λA>1,则△ABC为钝角三角形.
( )
(2011年台州市初中毕业生学业考试数学试题)
1 此题的“前生”
此题的“前生”为2003年安徽省数学中考试题的第24题:

图4
例2如图4,等腰三角形与正三角形的形状有差异,我们把等腰三角形与正三角形的接近程度称为“正度”.在研究“正度”时,应保证相似三角形的“正度”相等.设等腰三角形的底和腰分别为a,b,底角和顶角分别为α,β,要求“正度”的值是非负数.
学生甲认为:可用|a-b|来表示“正度”,|a-b|的值越小,表示等腰三角形越接近正三角形.
学生乙认为:可用式子|α-β|来表示“正度”,|α-β|的值越小,表示等腰三角形越接近正三角形.
探究(1)他们的方案哪个较合理,为什么?
(2)对你认为不够合理的方案,请加以改进(给出式子即可).
(3)请再给出一种衡量“正度”的表达式.
此题构思之妙,让人拍案叫绝!该题给笔者的感受有以下4点:
(1)课改理念到位.新课程改革中一方面要关注学生创新意识和创新能力的培养,关注学生自我学习能力的养成;另一方面既要重视结果性评价,也要重视过程性评价.该题很好地体现了课改理念,值得一提的是,本题在如何考查学生“发现问题和提出问题能力、分析问题和解决问题能力”给出了很好的样板.
第(1)小题要求学生能从已知中发掘出“正度”定义的合理性,即相似三角形“正度”的不变性.这对学生的发现问题能力进行了有效的考查.第(2)小题要求考生对不合理的方案能加以修正,正是对学生分析问题和解决问题能力的很好考查.第(3)小题直接考查学生提出问题的能力.
(2)背景熟悉明了.对于三角形、等腰三角形、正三角形的概念在义务教育数学课程第一、二学段就有介绍,三角形相似则在第三学段出现,因此这样的背景对学生来说是熟悉的.
(3)梯度设置合理.试题解决过程的思维呈线性上升,环环相扣.要解决第(2)小题,需有解决第(1)小题的能力.而第(3)小题更是一个综合的要求,只有透彻理解“正度”的概念,才有可能提出新的“正度”表达方式.
(4)构思可以类比.类比是发现和提出新问题的重要途径.命题也是如此,类比是其常用的法宝.该题给命题者留有很大的创造空间.如三角形类比为四边形、五边形等.接近度适用的范围就很广了,是极限的雏形.等腰三角形与正三角形接近度可类比一般三角形与等腰三角形接近度,正是源于这样的想法,才构造出例1.
2 此题的今世
此题的“十月怀胎”过程有点曲折,差点“流产”,下面慢慢道来.
类比例2,设想命制一个关于一般三角形与等腰三角形接近度这样一个新定义的题.问题的任务具有一定的层次性,设计若干个由浅入深的问题,难度在0.5~0.6之间.各小题之间的联系紧密,问题的设置由易到难,环环相扣,要求学生对这个新概念有不同的认知需求.具体让学生经历阅读理解、计算、作图等一系列操作以及综合判断的过程,从而加深新定义的理解和应用.希望体现对过程与方法、数学思考、创新思维、学习能力的考查.这也是选拔性考试的需要.

图5

(具体解答略.)

三稿决定不出现偏度这个概念,这样有效地避免了对定义的望文生义,产生不必要的纠缠.
四稿对于这个比值作了一个特别的补充,这也是数学定义中经常采用的方法.增加“特别地,当点D,E重合时,规定λA=0”,主要考虑到当点D,E重合时,DE如何算的问题.
至于后面3个问题的设计,是关注学生的层次性,前面问题的解决将为后面的问题提供思路,思维的要求由低到高.其设计思路沿袭了2009年台州市初中毕业生学业考试数学试题第23题的形式.第(1)小题只要能理解这个定义,直接运用定义即可;第(2)小题是定义的逆向运用,对于定义的内涵要有更深层次的理解;第(3)小题要求对前2个小题进行概括和提炼,设计成是非题是为了降低难度,提高得分率,当然对于该小题的信度有微小的影响.
第(2)小题的难度也可调整,如果改变条件让画出的结果不唯一,或者附加另外一些条件都将增加思维的深度和广度.
第(3)小题若题论题,则不到对数学更高层次的解读.在第(3)小题中,3个命题囊括了锐角三角形、直角三角形、钝角三角,并且就用本题定义的比值来判定,更妙的是分类的界点是1,因此从形式上给人以数学美的享受.
第(3)小题更一般的结论如下:
①△ABC为锐角三角形⟺λA,λB,λC的值均属于区间(0,1)(特别地,当λA,λB,λC均为0时,△ABC为正三角形);
②△ABC为直角三角形⟺λA,λB,λC的值恰有一个为1,另2个比值小于1;
③△ABC为钝角三角形⟺λA,λB,λC的值恰有一个大于1,另2个比值小于1.
3 此题的未来
多数学生进入高中后,早已忘却初中阶段的试题.其实例1与高中教材中的圆锥曲线有相似之处.因为圆锥曲线分成椭圆、抛物线、双曲线,以离心率e与1的大小进行分类:椭圆的离心率0
从上述对一个题目编制过程的反思,对于新定义型试题的命制,所呈现的素材不能随意捏造,要符合数学内部系统的规范性、科学性、严谨性.问题设置也要符合学生的认知规律,只有充分考虑到以上各种因素,才能使这类试题既有助于推进命题技术的进步,又能为实施素质教育和培养创新能力带来新的导向.
