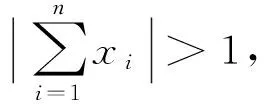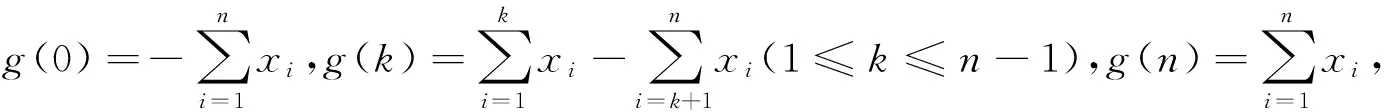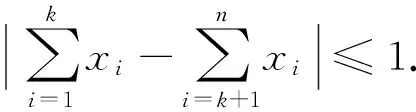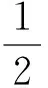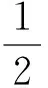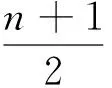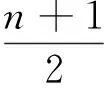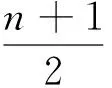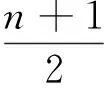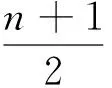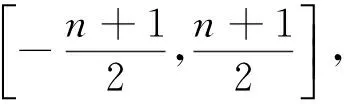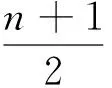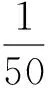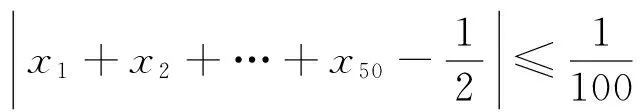一类不等式竞赛题的统一证明

●

(富阳中学 浙江富阳 311400)

一类不等式竞赛题的统一证明

●夏松明

(富阳中学 浙江富阳 311400)

若有一个人每次最多只能跳5米远，有一条河，河宽6米，此人想通过一系列的跳跃，从河的一边跳到另一边，则某个时刻，他一定落入河中.

上面的现象可引申为一个数学命题:数轴上有一区间[a,b](或(a,b))和一点集A={x1,x2,…}，满足x1

在数学竞赛中常出现与此命题相关的不等式证明问题.

(第5届中国西部数学奥林匹克竞赛试题)

|g(k+1)-g(k)|=2|xk+1|≤2，

(2012年全国高中数学联赛加试试题)

(第38届国际数学奥林匹克竞赛试题)

证明先给出一个引理：交换x1,x2,…,xn相邻2个数的位置可以得到其任何重排列y1,y2,…,yn.事实上，先考虑yn在x1,x2,…,xn中的位置，不断地交换2个相邻位置把yn往后面调整，直到yn调到最后一个数，依次类推，再考虑yn-1在x1,x2,…,xn的位置，不断地交换2个相邻位置把yn-1往后面调整，直到yn-1调到倒数第2个数.引理证毕，下证本题.

|y1+2y2+…+nyn+yn+2yn-1+…+ny1|=(n+1)|y1+y2+…+yn|=n+1,

交换2个相邻的数，即(yk,yk+1)→(yk+1,yk)，有

|y1+…+kyk+(k+1)yk+1+…+nyn|→|y1+…+kyk+1+(k+1)yk+…+nyn|,

又

|yk+1-yk|≤|yk+1|+|yk|≤n+1，

每次交换后，计算式的差距不超过n+1.由引理知，通过有限次交换，我们可以从y1+2y2+…+nyn到达yn+2yn-1+…+ny1，则其中必有一个交换，使得相对应的排列y1′,y2′,…，yn′有

因此，y1′,y2′,…yn′即为所求.

下面考虑交换2个相邻位置如下(为了节省篇幅，下面书写中，有时一下子交换多次)：

x1,…,x50,x51,…,x100↔x1,…,x49,x51,x50,x52,…,x100↔x1,…,x48,x51,x49,x52,x50,…,x100↔x1,…,x47,x51,x48,x52,x49,x53,x50,x54,…,x100↔…↔x51,x52,…,x100,x1,x2,…,x50.

[1] 单墫，熊斌.多功能题典：高中数学竞赛[M].上海：华东师范大学出版社，2013.