数学思维的5个品质——以2013年中考典题的破解为例

●

(晋州市实验中学 河北晋州 052260)

数学思维的5个品质
——以2013年中考典题的破解为例

●苑建广

(晋州市实验中学 河北晋州 052260)

数学与思维犹如一对夫妻，共同演绎着千古不朽的神话.“数学是思维的体操”，数学活动的核心是思维活动，数学的存在和发展离不开思维，都要通过思维来表现.反过来，数学又是思维的工具.在探索、研究和应用数学的过程中，思维品质也在发生着量和质的变化，并因此标志了数学修养之深浅.本文对数学思维品质的5个方面进行剖析，并附例以2013年中考典题.望各位同仁窥斑见豹，体味数学思维的无穷魅力.

1 思维的深刻性

思维的深刻性是指在分析和解决问题的过程中，能够透过表面现象认识和把握问题的实质及其相互关系，揭示规律，追根溯源，或将已有方法和结论拓展、变换、推广，得到更深刻的结果，谓之“思维的洞察力和穿透力”.思维的深刻性是一切思维品质的基础，主要表现为以下几个方面：

(1)对数学概念理解透彻，形成科学合理的概念域和概念系；对数学事实掌握清楚，形成科学合理的命题域和命题系.头脑中内化的数学知识是系统化和网络化的，犹如一棵倒挂的树：各知识点在这个网络中处于一定位置，知识点之间呈现出可推理的结构关系，并因此蕴含了思维方法和策略.

(2)具备良好的数学交流能力和符号意识，可以自如地将其他语言等价翻译为数学语言，发现或抽象出数学模型，实现横向或纵向数学化.

(3)能自觉运用分析、比较、抽象、概括等思维操作，发现形异质同的数学对象之间的内在联系.

(4)即使解决问题的条件不是明确给定的，也能不受表面现象的困扰，从表象中挖掘隐含条件，为解决问题作出适当的铺垫.

(5)在解决具体的问题后，能主动自觉地去寻找具有普遍意义的方法、模式，将思想、方法、结论等概括、迁移、推广到一般情境中去.

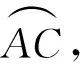
(2013年山东省烟台市数学中考试题)

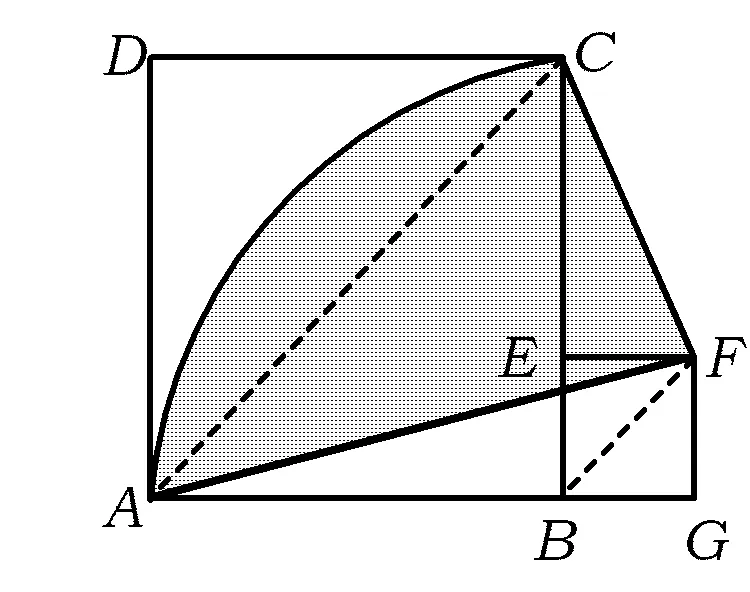
图1

分析通常采用割补法，化非标准图形为标准图形，按“S阴=S扇形BAC+S正方形EFGB+S△CEF-S△AGF”求解.设正方形EFGB的边长为a，则

CE=4-a，AG=4+a，

于是

这个结果正好是扇形BAC的面积！那么，图中阴影面积是否能转化成扇形BAC的面积呢？容易想到联结BF,AC，易证BF∥AC，可见△ACB与△ACF是“同底等高”的，面积也相等，于是S阴=S扇形BAC，思路被大大优化.从中可知，阴影部分的面积与点E在线段BC上的位置(即正方形EFGB的大小)无关，是定值4π.继续思考，还可发现：

变式1如图2，把“点E在BC上”变为“点E在BC的延长线上”时，亦可得阴影部分的面积为4π.

图2 图3 图4

变式2如图3，当四边形ABCD和四边形EFGB均为平行四边形，且2个平行四边形相似，点E在射线BC上运动时，阴影部分的面积为平行四边形ABCD面积的一半.

变式3如图4，当四边形ABCD和四边形EFGB均为等腰梯形，且2个等腰梯形相似，点E在射线BC上运动时，阴影部分的面积等于△ABC的面积.

变式4如图5，当△ABC∽△EDB,点E在射线BC上运动时，阴影部分的面积等于△ABC的面积.

这也是此类图形的本质所在.

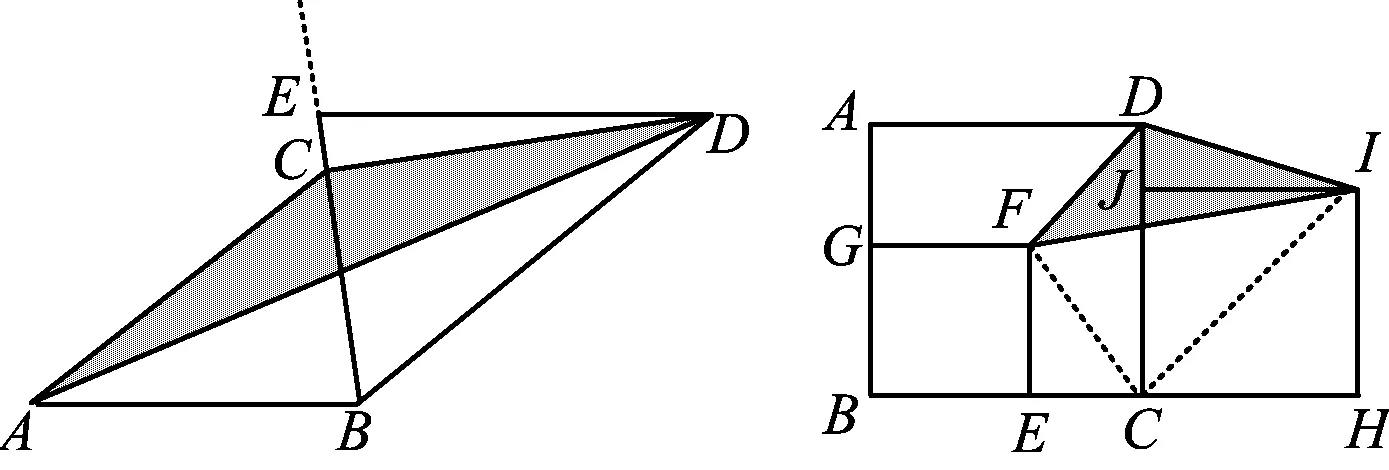
图5 图6

变式5如图6，有3个正方形ABCD，BEFG和CHIJ，其中正方形ABCD的边长是a，正方形BEFG的边长是b，当点J在射线CD上运动时，阴影部分的面积等于△CDF的面积,值为a2-ab.

继续梳理上述问题的辩证关系，按照“从特例到一般”的顺序，层层设问，不断触及问题的本质，就能设计出一系列非常优秀的探究性问题.

溯本穷源悟真知.在数学学习中，善于透过现象看本质，有利于实现对数学概念和命题的深刻理解.

2 思维的灵活性

思维的灵活性是指因题制宜，活用有关知识多角度寻求问题解决途径的能力，谓之“思维的发散力和变通力”.主要表现为以下几个方面：

(1)思维起点灵活.善于全面地看问题，能从与题目相关的各种角度和方向去考虑问题.

(2)心理转向容易.从正向思维转为反向思维，特别是对概念正反关系的认识、公式的正反运用、定理与逆定理的灵活使用、解题中分析法与综合法交替使用时表现自如.

(3)思维转换迅速.可以不受先前解题方法的影响，克服思维定势的消极作用及自我心理限制，遇机而变，及时调整思路、方法、技巧，不拘一格、有的放矢地解决问题.

(4)思维过程中善于转化.可以很容易地化生为熟，把几个部分看成一个整体，或把一个整体分成几个部分，也就是聚零为整，化整为零.

(5)概括、迁移能力强.运用规律熟练，善于组合分析，思维有弹性、能跳跃，既能注意把握事物的整体，又不忽视重要的细节，能够从多层面上捕捉有效信息，广泛地对比、联想，在研究问题本身的同时，拓展到相关问题.

图7

例2从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图7所示的零件，则这个零件的表面积为______．

(2013年山东省枣庄市数学中考试题)

分析整体观察图形，利用“平移”实现对问题解决过程的优化，把求“表面积”的问题转化成求“从上、下、左、右、前、后6个方向看到的视图面积之和”的问题，极易得到这个零件的表面积为6×(2×2)=24.此时，视图成为一种解题的工具，只要是从毛坯的一角，挖去一个(任意)长方体，则其表面积均为24，是不变的.解法的趣味性和灵活性都很强.

3 思维的独创性

思维的独创性是指思维的结果相对于(自己)已有的认识成果来说，具有独特性和新颖性，是最难得的思维品质，谓之“思维的发现力和创造力”.主要表现为以下几个方面：

(1)从事数学活动时，能对数学对象进行独立的思考，善于发现、提出、分析、解决问题，勇于创新，敢于突破常规的思考方法和解题模式，大胆提出新见解和采用新方法

(2)能从与众不同的全新角度观察问题，能在貌似平常的信息中发现不寻常之所在，从而发现隐含的特殊联系，产生与他人不同的思路和结论.

(3)富于联想.在解题时主动联系数学的不同分支、其他学科以及生活实际，以至思维跳跃，经常产生有别于常规的、正统的、创造性的想法.

例3某数学活动小组在作三角形拓展图形，研究其性质时，经历了如下过程：

(1)操作发现：

在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图8所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，联结MD和ME，则下列结论正确的是______.

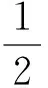
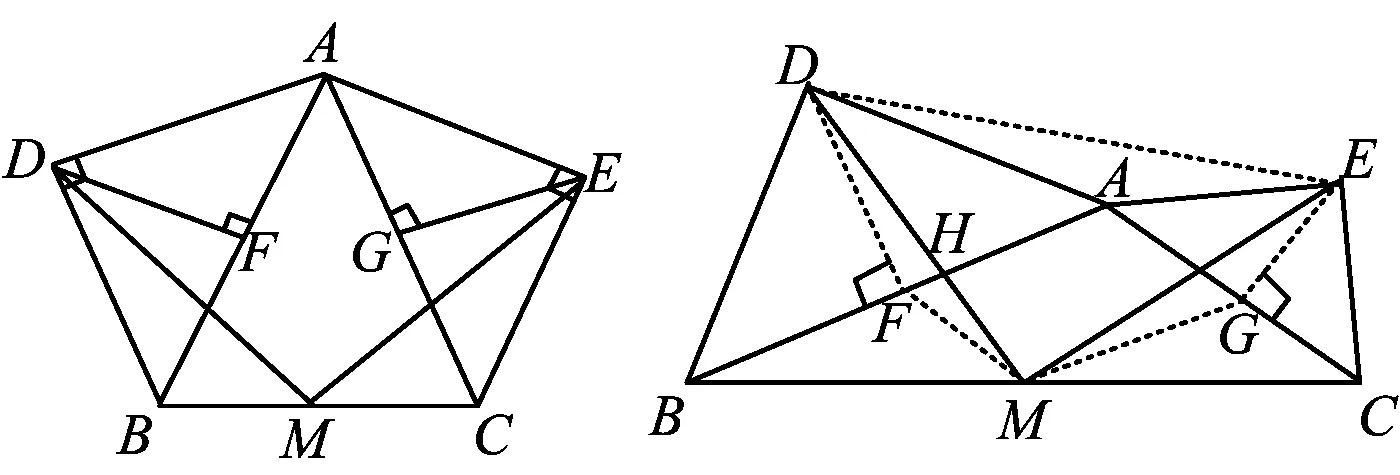
图8 图9

(2)数学思考：

在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图9所示，M是BC的中点，联结MD和ME，则MD和ME具有怎样的数量关系和位置关系？请给出证明过程.

(3)类比探索：

在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图10所示，M是BC的中点，联结MD和ME，试判断△MED的形状．

(2013年江西省南昌市数学中考试题)

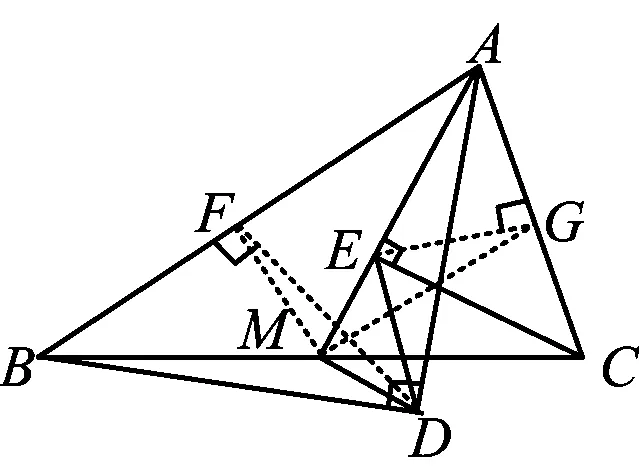
图10

分析常规思路自然是按部就班，依次完成题目设问，且通常是分别对MD和ME的数量关系和位置关系予以说明.但是，显然图8是图9的一种特殊情形，而图9与图10又属于并列情形，题目本身呈现出“从特例推向一般”、“从一种情形(图9中向△ABC的外侧作等腰直角三角形)向另一种情形(图10中向△ABC的内侧作等腰直角三角形)拓展”的命题模式.参透了这一点，便能作如下处理：

欲证“△DME是等腰直角三角形”，若能证出“∠MDE=∠MED=45°”，则问题得以突破.

如图9，取AB,AC的中点F,G，联结DF,FM,EG,GM,DE. 易知∠FDA=∠GEA=45°，于是转为证

∠ADE=∠FDM，∠AED=∠GEM.

设AB=2a,AC=2b，易得

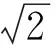
于是

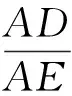
又易证 ∠DAE= 270°-∠BAC=

(180°-∠BAC)+90°=

∠AFM+∠AFD=∠DFM,

于是

△DAE∽△DFM,

故

∠ADE=∠FDM，

同理可证

∠AED=∠GEM.

到此，思路被打通.将其条件强化，则第(2)小题自然得证.

将之迁移到图10中，易知∠FDA=∠GEA=45°，于是转为证

∠ADE=∠FDM，∠AED=∠GEM.

仍设AB=2a,AC=2b，可得

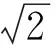
于是

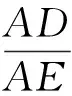
又易证 ∠DAE= (∠DAB+∠EAC)-∠BAC=

90°-∠BAC=90°-∠MFB=

∠DFM，

于是

△DAE∽△DFM，

故

∠ADE=∠FDM，

同理可证

∠AED=∠GEM.

到此，思路再次被打通.

如此处理，显然超出了命题人所料，是极具创新味道的.正是善于查“平凡中之异象，平静中之波澜”，才成就了创新解法.由于特殊情形往往存有无关宏旨的枝节或表面现象，容易掩盖问题的实质，而一般情形则更能明确地表达问题的本质.因此，有时面对一般化的问题可能更容易求解.就此，希尔伯特有言：“在解决一个数学问题时，如果我们没有获得成功，原因常常在于我们没有认识到更一般的观点，即眼下要解决的问题不过是一连串有关问题的一个环节.”

4 思维的批判性

思维的批判性是指在思维活动中独立思考，善于提出疑问，敢于发表不同的看法，严格客观地评价思维的结果和精细地检查思维过程的品质，谓之“思维的诊断力和甄别力”.主要表现为以下几个方面：

(1)不会不经思考地附和他人的意见，能坚持自己的合理看法，善于发现问题，明辨是非，不迷信书本和专家，敢于向教师提出质疑;

(2)能够比较不同对象之间的差异和相似性，辨析容易混淆的概念与形式，对数学对象进行合理分类;

(3)能评估信息资源的可靠性，判断从一个结论导出另一个结论的充分性，因而发现解题过程或结论中的错误;

(4)能在有多种合情思路的情况下，对各种解题思路、方法、策略进行比较，选择更为合理的方案，从而找出最佳的方法或结论;

(5)在解题时能对全过程进行监控，经常回头审视自己的解题过程，进行有意识的自我调节，在自我检查中修正论证的过程和结论．

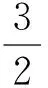
(2013年福建省龙岩市数学中考试题)

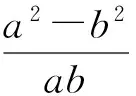
题目难度较大.良好的“数感”固然是重要的，但不断地对猜想所得进行检验和修正，以决定继续进行下去，还是另觅他径，更显重要.思维批判的对象不仅是他人，更是自己.善于自我监控解答过程，“思必有的、有据、有序”，而不是瞎碰乱试，就可在一定程度上避免更多失误，省时省力.

5 思维的敏捷性

思维的敏捷性是指智力活动的速度，在处理问题和解决问题的过程中，能够适应迫切的情况来积极地思考，并迅速地作出判断，谓之“思维的自动化和果断力”.主要表现为以下几个方面：

(1)能够较快且正确地完成对题目信息的理解;

(2)能够自觉地运用简便方法，对数字进行快速运算，且“感觉良好”;

(3)能够迅速地判别出题目的模式，从而缩短解题时间;

(4)能对最近做过的题目有清晰的记忆，迅速反应出解题过程及结果;

(5)能够迅速判断，像电脑或机器一样自动、果断地执行，在时间紧迫的情况下作出继续下去或是放弃进行的决策.

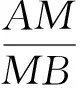
请根据以上结论，解答下列问题：

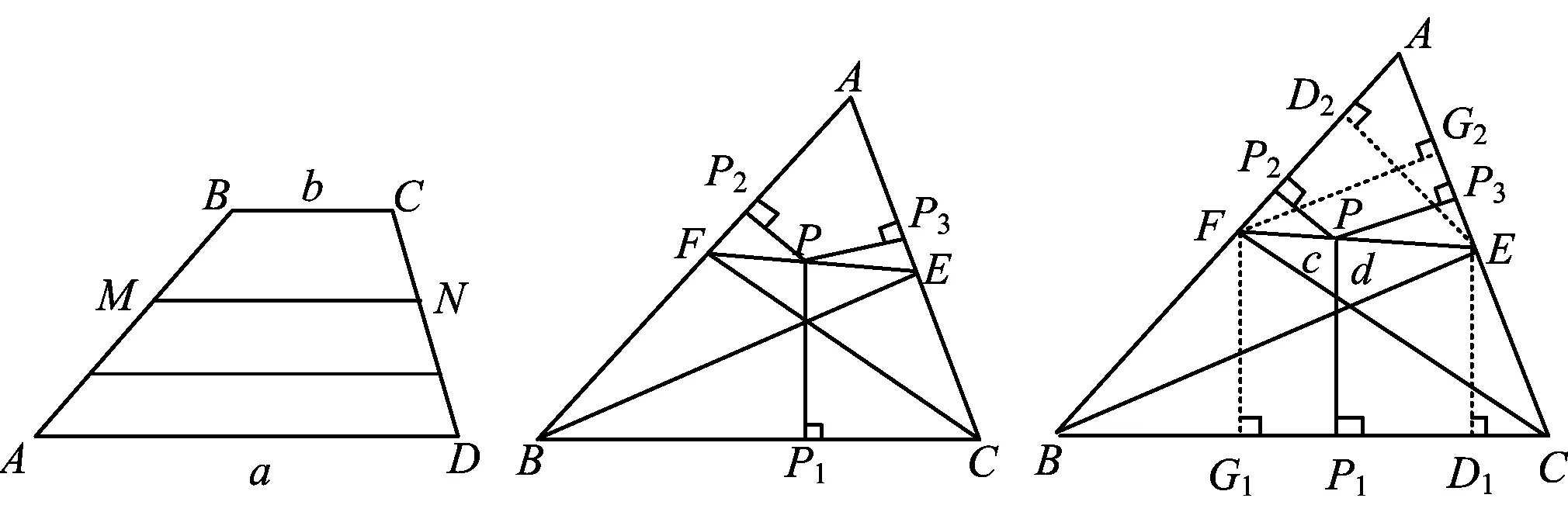
图11 图12 图13

如图12和图13，BE,CF是△ABC的2条角平分线，过EF上一点P分别作△ABC三边的垂线段PP1,PP2,PP3，交BC于点P1，交AB于点P2，交AC于点P3.

(1)若点P为线段EF的中点，如图12，求证：PP1=PP2+PP3；

(2)若点P在线段EF上任意位置时，如图13，试探究PP1,PP2,PP3的数量关系，并给出证明.

(2013年四川省乐山市数学中考试题)

分析题目给出了一个新命题(几何模型)，思维的重点应放在运用新命题解决新问题上.如何“引经据典”，快速完成向模型的化归，有意识地把新知识、新模型移植转用到新对象上是解决问题的关键.

运用观察、测量、比较、计算等手段可以“合情”地猜想第(1)小题中之结论可以迁移到第(2)小题中.因此这里我们直接面对第(2)小题，待之证明结束后，将条件强化，则第(1)小题自然得证.结合题设和待证结论，对比图形构成特点，容易想到如图13所示的辅助线.设PF=c，PE=d，在梯形EFG1D1中，易得

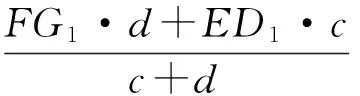
又三角形可以看作退化的梯形(上底为0)，在△FED2和△EFG2中，易得

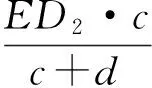
而ED1=ED2,FG1=FG2,故

PP1=PP2+PP3.

实际上，我们虽然分述了数学思维的5个品质，并分别附例诠释，但是这些品质之间并不是相互分离和隔裂的.恰恰相反，它们是相互渗透、联系和制约的统一体.深刻性是所有思维品质的基础，在其支撑下进行发展，避免思维定势的负面影响，灵活处理，才能产生独创性见解.加上周密地思虑、批判性地认知和合理地自我监控与调节思维过程，就能形成全面准确的判断，揭示数学本质和规律.而只有实现了深刻的理解、灵活而富有创造性地思考以及批判性地审问，才能达到心领神会、融会贯通，从而生发出真正的敏捷性，全面提升思维品质，享受数学思维的无限乐趣.

对数学思维的研究永远是没有止境的.本文仅仅是在专家理论研究的基础上补例诠释，为中学数学教学提供借鉴.不妥之处，诚请不吝赐教.

[1] 中华人民共和国教育部制定.全日制义务教育数学课程标准[M].北京:北京师范大学出版社，2011.

[2] 鲍建生，周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009.

[3] 章建跃.数学教育心理学[M].北京:北京师范大学出版社,2006.

[4] 苑建广.管窥数学思维的若干策略[J].数理化学习:初中版，2012(12):1-9.

[5] 苑建广.信息转化——问题解决的核心策略[J].中国数学教育:初中版，2012(3):45-48.

[6] 苑建广.精心雕琢命题方式切实考查数学能力——2011年中考数学特色题归类赏析[J].教育实践与研究:B版，2011(11):7-12.