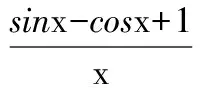三角函数的图像与性质

● (学军中学 浙江杭州 310012)

三角函数的图像与性质

●叶燕忠(学军中学 浙江杭州 310012)

1 命题趋势

近几年高考对三角函数部分的考查，在内容、题量、分值3个方面均保持稳定，难度适中，重点考查考生的演绎推理能力、计算能力和综合应用知识解决问题的能力.在复习时要注意基础知识的理解和落实.

2 典例剖析

题型1已知图像求表达式

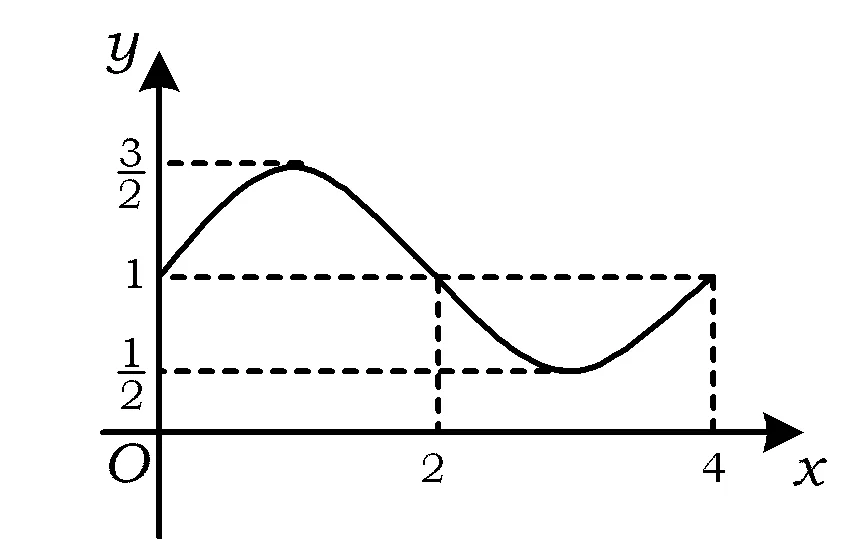
图1

例1函数f(x)=Asin(ωx+φ)+B的图像如图1所示，则S=f(0)+f(1)+f(3)+…+f(2 011)的值是______.

观察f(n)的规律得

f(1)+f(2)+f(3)+f(4)=4，

从而

S= 2 008+f(2 009)+f(2 010)+f(2 012)=

2 008+f(1)+f(2)+f(3)=2 011.

评注本题考查了函数的表达式和周期性，在写出函数表达式的情况下，f(0),f(1),f(2),…,f(2 011)的取值呈周期性.

题型2三角函数图像的变换

例2直线y=5与曲线C:y=msinx+n(m>0),x∈[0,2π]交于点A，B，直线y=-1与曲线C交于点C，D，且|AB|=|CD|，则

( )

A.n=2,m>3 B.n=2,m=3

C.n=3,m>2 D.n,m的值均不确定

答案A.

分析本题重点考查函数的图像、最值等三角函数的核心内容，可从“有交点”的角度入手，求得函数最大值为m+n.图像与y=5有交点，只需满足

函数最小值为m-n，图像与y=-1有交点，只需满足-m+n<-1，即

由式(1)，式(2)得m>3.故选A.

另一方面，需要思考如何保证“|AB|=|CD|”这一条件.由对称性，要使2条直线l1:y=a,l2:y=b被y=msinx截得的线段相等，必须保证l1与l2关于x轴对称，即a+b=0.由y=msinx图像向上或向下平移得到y=msinx+n的图像，直线l1与l2在相同的平移下，得到直线y=a+n和y=b+n这2条直线分别对应y=5与y=-1，因此a+b+2n=4，解得n=2.

题型3三角函数的单调性

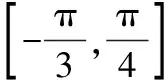
答案0<ω≤2.

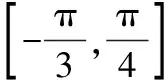
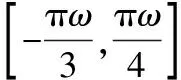
评注本题属基本题，主要考查y=sinωx的单调性，尤其注意ω的正负对单调性的影响.

例4函数f(x)=Msin(ωx+φ)(ω>0)在区间[a,b]上是增函数，且f(a)=-M，f(b)=M,则函数g(x)=Mcos(ωx+φ)在[a,b]上

( )

A.是增函数 B.是减函数

C.可取最大值MD.可取最小值-M

答案C.

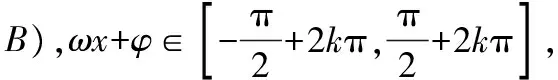
分析2此题可由特殊值法求解，取M=ω=1，φ=0易得选项C正确.

题型4三角函数的最值

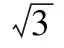
分析化简表达式,得

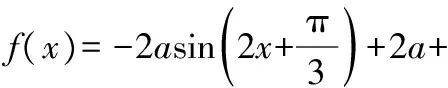
y=-2at+2a+b,

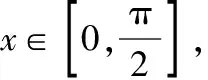
当a>0时，y=-2at+2a+b为减函数，即

解得

a=2,b=-5.

当a<0时，y=-2at+2a+b为增函数，即

解得

a=-2,b=1.

题型5三角函数的周期性、对称性

( )

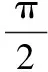
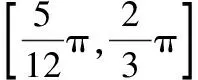
D.f(x)的最大值为A

答案C.

分析形如f(x)=Asin(ωx+φ)的图像特点为“在对称轴处函数值取最大或最小，在对称中心处函数值为0”.

由T=π得ω=2，即

f(x)=Asin(2x+φ)，

又

从而

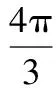
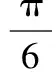
故选C.

题型6三角函数与解三角形

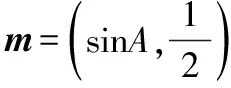
(1)求角A；

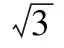
分析(1)由m,n共线，得

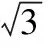
化简得

从而

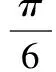
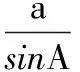
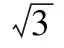
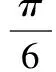
3 精题集萃

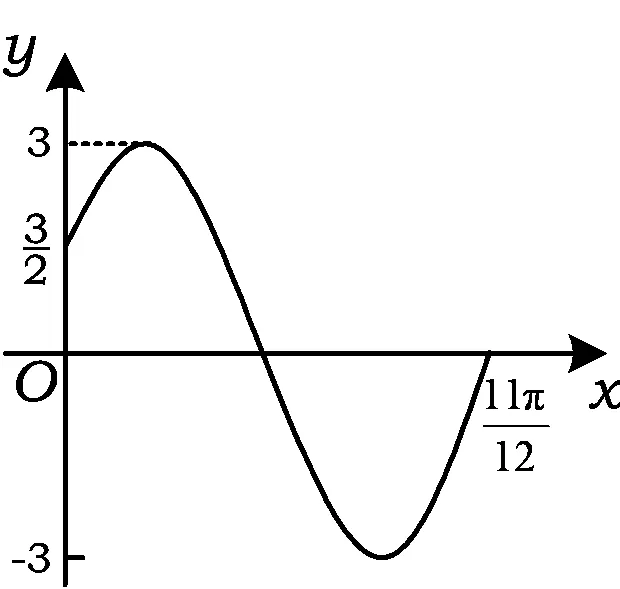
图2

( )

( )

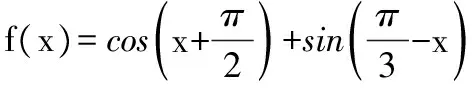
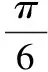
A.sinxB.-sinxC.1 D.tanx

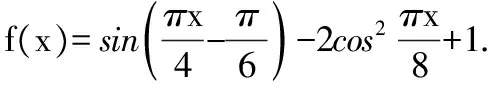
(1)求f(x)的最小正周期;

6.函数f(x)=ax+cosx，x∈[0,π],若f(x)≤1+sinx,求a的取值范围.

参考答案

2.C 3．A

6.易知当x=0时，不等式成立;当x∈(0,π]时，分离变量得