概率与统计问题的高考走势
2013-10-26衢州市第二中学浙江衢州324000
● (衢州市第二中学 浙江衢州 324000)
概率与统计问题的高考走势
●杨樟松(衢州市第二中学 浙江衢州 324000)
纵观全国和各省、市近几年的数学高考题,笔者发现新课程标准实施以后,高考加强了对数学应用问题的考查.概率与统计不仅是现代公民应具备的最基本的数学知识,而且与实际的联系非常密切,对学生解决非确定性数学问题的能力进行有针对性的考查,同时又是大学概率论与统计学的基础,起到了承上启下的作用.新课程强调数学的基础性、现实性,重视素质教育与高考的兼容性,概率统计的教学内容恰好是一个很好的载体,已成为高考的热点之一.
1 考点回顾
概率是研究随机现象规律的学科,统计是研究如何合理收集、整理、分析数据的学科.统计的主要内容有:抽样方法、用样本估计总体、正态分布;概率的主要内容有:古典概型的概率、互斥事件有一个发生的概率、对立事件的概率、独立事件同时发生的概率、独立重复试验的概率,以及取有限个值的离散型随机变量的分布列、均值、方差、两点分布、二项分布、超几何分布等.
高考对这部分内容的考查往往注重联系实际、贴近生活.文科重点考查古典概型的概率及样本的数字特征、频率分布直方图;理科则重点考查以相应的概率知识为基础的有关离散型随机变量分布列、均值、方差的知识.
2 命题走势
文科要求相对较低,以小题的形式出现的可能性较大.概率部分主要考查以古典概型为主的概率,统计则主要考查抽样方法、由频率分布直方图计算频率及样本的数字特征.理科除了2011年以小题的形式出现以外,其余年份都是以解答题并设计多个小题的形式出现,重点考查离散型随机变量的分布列、均值、期望、方差等.通常以考生熟悉的生活背景为载体,以排列组合和概率知识为工具,考查对概率事件的识别与概率的计算.
3 典例剖析
例1袋中共有6个除了颜色外完全相同的球,其中1个红球、2个白球和3个黑球.从袋中取2个球,这2个球的颜色为一黑一白的概率等于
( )
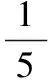
(2012年安徽省数学高考文科试题)
分析由于每个球被取到的可能性相等,且基本事件的总数是有限的,可知该题属于古典概型,因此可以采用列举法求解.

评注解决古典概型问题的关键是要明确:①基本事件是什么?②试验是否等可能?③基本事件总数是什么?④事件中包含多少个基本事件?

(1)甲获胜的概率;
(2)投篮结束时甲的投球次数ξ的分布列与期望.
(2012年重庆市数学高考理科试题)
分析因为甲、乙2人投篮是相互独立的,所以应利用相互独立事件同时发生概率的方法解决.
解设Ak,Bk分别表示甲、乙在第k次投篮投中,则

(1)记“甲获胜”为事件C,由互斥事件有一个发生的概率与相互独立事件同时发生的概率计算公式知

(2)ξ的所有可能取值为1,2,3.由独立性知
综上所知,ξ的分布列如表1所示.

表1 ξ的分布列
从而

评注本题主要考查互斥事件概率的求解、离散型随机变量的分布列与期望,关键是确定变量的取值,理解变量取值的含义.同时,要注意在解决概率问题时要规范解答,有必要的文字叙述,不能只有数字和符号.
例3假设甲、乙2种品牌的同类产品在某地区市场上销售量相等,为了解它们的寿命,现从这2种品牌的产品中分别随机抽取100个进行测试,结果统计如图1和图2所示.
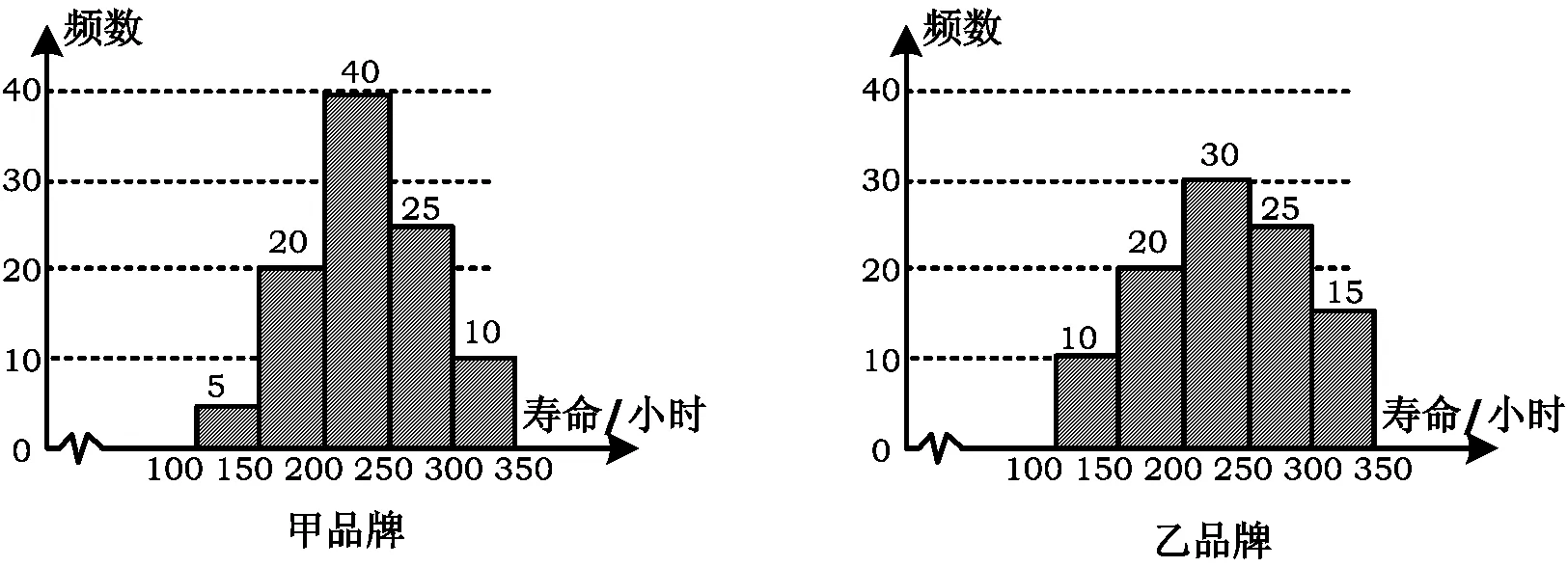
图1 图2
(1)估计甲品牌产品寿命小于200小时的概率;
(2)这2种品牌产品中,某个产品已经使用了200个小时,试估计该产品是甲品牌的概率.
(2012年陕西省数学高考文科试题)
分析问题(1)先从频数分布图中得到甲产品寿命小于300小时的个数,与总数相比求出概率.问题(2)先求出已使用了200小时的产品总数,再找到甲品牌的个数,二者相比即可得到结论.

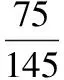
评注本题主要考查读频率分布直方图的能力和利用统计图获取信息的能力,用样本的频率分布估计总体分布的思想,关键在于能读否懂频率分布直方图.
例4袋中有大小均匀的3个红球和6个白球,现从中有放回地摸球,每次摸一个,有3次摸到红球即停止.
(1)求恰好摸5次停止的概率;
(2)记5次之内(含5次)摸到红球的次数为ξ,求ξ的分布列与期望.
分析由于本题是“有放回”地摸球,因此可以用独立重复试验求概率的方法求解.



随机变量ξ的分布列如表2所示.
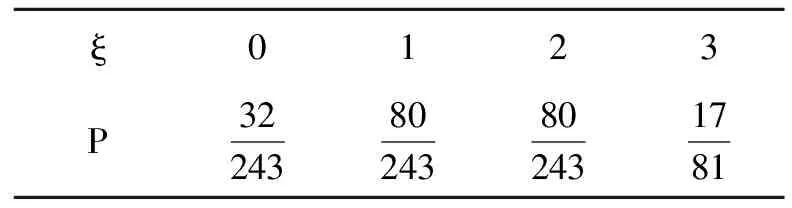
表2 ξ的分布列
从而数学期望为
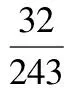
评注在解决摸球、摸奖等古典概型问题时,要特别注意分清“有放回”与“无放回”、“有序”与“无序”等条件的影响.
例5甲、乙2位同学参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,绘制成茎叶图如下:

甲乙9875842180035539025
(1)指出学生乙成绩的中位数,并说明它在乙组数据中的含义;
(2)现要从中选派一人参加数学竞赛,从平均成绩和方差的角度来考虑,你认为派哪位学生参加更合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的3次数学竞赛进行预测,记这3次成绩中高于80分的次数为ξ,求ξ的分布列与期望.
分析由于学生甲在今后的3次数学竞赛中分数是否高于80分的事件每次相互独立,因此成绩中高于80分的次数为ξ服从二项分布,故可以采用二项分布求概率的方法求解.
解(1)学生乙成绩的中位数为84,它是这组数据中最中间位置的一个数或最中间位置2个数的平均数,中位数可能在所给的数据中,也可能不在所给数据中.
(2)派甲参加比较合适,理由如下:
其中,Structurei,t表示旅游产业结构升级,Convergi,t表示文化与旅游产业融合;Mediatori,t表示中介变量,包括文化与旅游消费需求(Demandi,t)、技术创新(Techi,t)、文化与旅游业协同集聚(Clusteri,t);Controlsi,t表示控制变量,包括市场化水平(Marketi,t)、人力资本(Labori,t)、政府支出(Governi,t)、贸易开放(Openi,t);α、β、γ、φ为系数向量,εi,t为随机误差项。
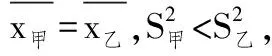
所以甲成绩比较稳定,派甲参加比较合适.
(3)记“甲在一次数学竞赛中成绩高于80分”为事件A,则
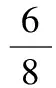
依题意,得
从而
因此ξ的分布列如表3所示.
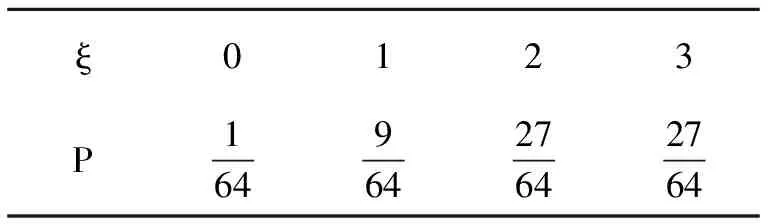
表3 ξ的分布列
从而

或
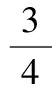
评注本题主要考查了读茎叶图的能力、二项分布的概念.判断一个随机变量是否服从二项分布,关键是:(1)独立性,即在一次实验中,事情发生与不发生二者必居其一;(2)重复性,即实验独立重复地进行了n次.
4 精题集萃
1.一个坛子里有编号为1,2,…,12的12个大小相同的球,其中1到6号球是红球,其余的是黑球.若从中任取2个球,则取到的都是红球且至少有1个球的号码是偶数的概率是
( )
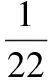
2.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一件发生的概率是
( )

3.投掷2颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n-mi)为实数的概率为
( )

4.由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差等于1,则这组数据为________.
(2012年广东省数学高考文科试题)
5.在4张卡片上分别写有数字2,3,4,5,将它们混合,然后再任意排成一行,则得到的4位数能被2或5整除的概率是______.
7.乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.在甲、乙的一局比赛中,甲先发球.
(1)求开始第4次发球时,甲、乙的比分为1∶2的概率;
(2)ξ表示开始第4次发球时乙的得分,求ξ的期望.
(2012年全国数学高考大纲卷理科试题)
(1)求n的值.
(2)现从甲、乙2个盒子各随机抽取1个小球,抽得红球的得分为其标号数;抽得黑球,若标号数为奇数,则得分为1,若标号数为偶数,则得分为0.设被抽取的2个小球得分之和为ξ,求ξ的数学期望.
参考答案
7.解记Ai表示事件:第1次和第2次这2次发球,甲共得i分,i=0,1,2;
A表示事件:第3次发球,甲得1分;
B表示事件:开始第4次发球时,甲、乙的比分为1∶2.
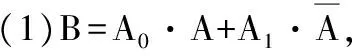
0.16×0.4+0.48×(1-0.4)=
0.352.
(2)P(A2)=0.62=0.36,ξ的可能取值为0,1,2,3,则
P(ξ=0)=P(A2·A)=P(A2)P(A)=0.36×0.4=0.144,
P(ξ=2)=P(B)=0.352,

P(ξ=1)=1-P(ξ=0)-P(ξ=2)-P(ξ=3)=0.408,
故
Eξ=1.400.




故

