一个函数问题的多种解法研究

●

(徐州市第三十五中学 江苏徐州 221003)

一个函数问题的多种解法研究

●鹿存伟

(徐州市第三十五中学 江苏徐州 221003)

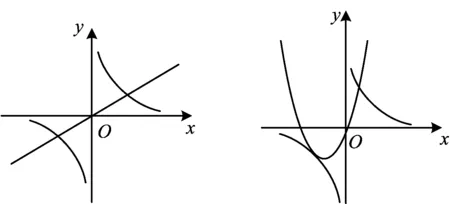
图1 图2

解得

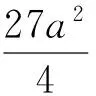
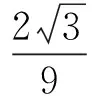
解后反思所给2个函数都是基本初等函数，可以直接作出它们的图像，研究图像何时有2个不同的公共点，并寻求参数a满足的关系式，从而求解出参数a的取值范围．由于函数g(x)的解析式中含有参数，需讨论其图像的各种可能性．

图3 图4

(1)当a=0时，如图3，符合题意.

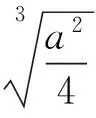
从而

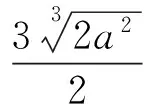
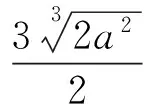
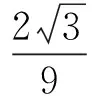
解后反思根据函数与方程的关系，把条件转化为另2个基本初等函数的图像有2个不同的公共点的问题，根据这2个函数的图像来求解．转化后，其中一个函数是一次函数，其图像是一条直线，在分析2个图像的公共点时，利用直线的优势，一目了然，便于得到各种可能性及寻求参数a满足的关系式，使问题得解．

图5 图6

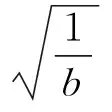
(2)当a≠0时，设函数h(x)=ax3+bx2-1，则

h′(x)=3ax2+2bx=x(3ax+2b).

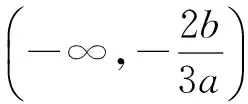
即

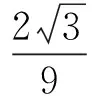
即

解后反思根据函数与方程的关系，把2个函数图像的公共点问题转化为一个函数的图像与x轴的公共点问题．利用导数研究该函数的单调性和极值，然后根据其图像，寻求参数满足的关系式，结合b∈(0,1)求解．求解过程中注意对参数进行分类讨论．

图7

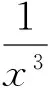
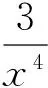
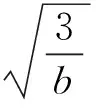
极小值为

解后反思根据函数与方程的关系及参变分离法，把2个函数图像的公共点问题转化为一个函数的图像和直线y=a的公共点问题．利用导数研究该函数的单调性和极值，由于实施了参变分离，其单调性简单明了，无需分类，然后根据其图像，易得参数满足的关系，结合b∈(0,1)求解．