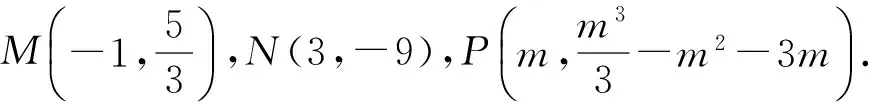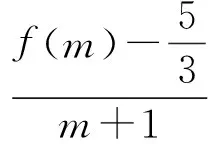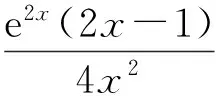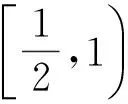例谈导数综合题中数形结合的应用
2013-10-26
●
(杭州市外国语学校 浙江杭州 310023)
例谈导数综合题中数形结合的应用
●张传鹏
(杭州市外国语学校 浙江杭州 310023)
纵观近几年全国各地区的数学高考,每年都有导数试题,且有一道大题考查利用导数研究函数的极值、单调区间、实际应用或证明不等式,尤其是试题中含有参数需要分类讨论时,使得本已抽象的问题更加复杂化.许多学生在学习和解答时,十分茫然,不知从何下手.其实在解决此类问题时,若能将抽象化为直观,并时刻给学生渗透“数形结合思想”,则问题可以变得更简单明了.
(2009年福建省数学高考理科试题)
解法1f′(x)=x2-2x-3=(x-3)(x+1),
得函数f(x)的单调递增区间为(-∞,-1)和(3,+∞),单调递减区间为(-1,3),因此
从而直线MP的方程为

联立
得
x3-3x2-(m2-4m+4)x-m2+4m=0,
线段MP与曲线f(x)均有异于M,P的公共点,等价于上述方程在(-1,m)上有根,即函数
g(x)=x3-3x2-(m2-4m+4)x-m2+4m
在(-1,m)上有零点.因为g(x)为三次函数,所以g(x)至多有3个零点,2个极值点,又g(-1)=g(m)=0,因此g(x)在(-1,m)上有零点等价于g(x)在(-1,m)上恰有一个极大值点和一个极小值点,即
g′(x)=3x2-6x-m2+4m-4=0
在(-1,m)上有2个不相等的实数根,即
解得
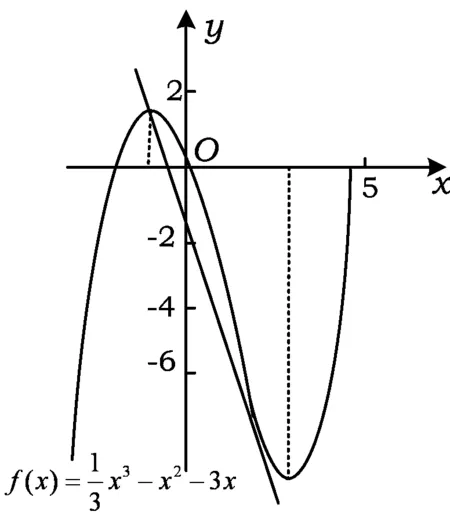
2 图1 又因为-1 解得m=2,因此满足题设条件的t的最小值为2. 评注本题给出了2种解法:解法1通过分析把问题转化为“当方程3x2-6x-m2+4m-4=0在(-1,m)上有2个不相等的实数根时求实数m的取值范围”,容易找到思路,但计算量大.证法2则巧妙地利用函数图像,通过分析知道当线段MP与曲线f(x)相切时,t取到最小值,使得问题简单明了,且计算量小,学生容易理解. 例2已知函数f(x)=(k2-klnx)ex(k为非零常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.当b>0时,若f(x)≥(1+a)x-exlnx+b在定义域上恒成立,求(a+1)b的最大值. 解法1f(x)≥(1+a)x-exlnx+b⟺ex-(a+1)x-b≥0,令h(x)=ex-(a+1)x-b≥0,则 h′(x)=ex-(a+1). 当a+1<1时,h′(x)>0,从而y=h(x)在x∈R+上单调递增,因此 h(x)>h(0)=1-b≥0, 即0 当a+1=1时,h′(x)>0,从而y=h(x)在x∈R+上单调递增,因此 h(x)>h(0)=1-b≥0, 即b≤1,此时(a+1)b的最大值为1. 当a+1>1时,由h′(x)>0⟺x>ln(a+1),h′(x)<0⟺x h(x)min=(a+1)-(a+1)ln(a+1)-b≥0, 即 b≤(a+1)-(a+1)ln(a+1), 从而 (a+1)b≤(a+1)2-(a+1)2ln(a+1)(其中a+1>1). 令a+1=t(t>1),设F(t)=t2-t2lnt(t>1),则 F′(t)=t(1-2lnt), 从而 解法2基本不等式法. 由f(x)≥(1+a)x-exlnx+b⟺ex-(a+1)x-b≥0,得 从而 因此 解法3数形结合法. f(x)≥(1+a)x-exlnx+b⟺ex-(a+1)x-b≥0,即ex≥(a+1)x+b在定义域上恒成立,则 a+1≥0. 当a+1=0时,(a+1)b=0. 当a+1>0时,如图2所示,设曲线y=ex,y=(a+1)x+b,2条曲线切点为P(x0,ex0),则 从而(a+1)b=ex0(ex0-x0ex0)=e2x0(1-x0), 图2 则 因此 评注本题给出了3种解法:解法1通过讨论求出(a+1)b的最大值,比较繁琐,学生不易想到,且运算量较大;解法2则巧妙地利用了基本不等式,再借助于导数,求出(a+1)b的最大值;解法3巧妙利用了2个函数图像相切的位置关系,求出了(a+1)b的最大值,思路简洁,学生容易理解. 例3设函数f(x)=x2-xlnx+2, (1)求f(x)的单调区间; 解(1)令g(x)=f′(x)=2x-lnx-1(x>0),则 故f(x)的单调递增区间是(0,+∞). F′(x)<0; 当x∈(1,+∞)时,G(x)>0,从而 F′(x)>0, 故 图3 解得 若要有2个交点,则必有k>1,故 数形结合思想,其实质是将抽象的数学语言与直观的图像结合起来,也就是对题目中的条件和结论既分析其代数含义又挖掘其几何背景,在代数与几何的结合上寻找解题思路.最常用的是“以形助数”的解题方法,其实质就是对图形性质的研究,使要解决的数的问题转化为形的讨论,实现“由一种代数形式转化为几何形式”的数学化归.从上面的探讨可以看出,在导函数的教学过程中,除了要加强数学基础知识的学习,还要学会用数形结合思想的方法来研究问题,从而提高学生的创新能力和实践能力. (本文系全国教育科学“十二五”规划2011 年度教育部重点课题“高中数学有效教学课例研究”(课题批准号:DHA110240)的阶段性成果.)