港口船舶牵引机械强度及稳定性分析

韩 龙， 钱 怡

(江南大学机械工程学院，江苏无锡214122)

船舶牵引机械是中大型港口常用的港口设备，其作用在于拉动货船沿岸边平行移动，便于装卸货物。由于该机械属悬臂细长结构，其强度、刚度和稳定性决定牵引机械的工作可靠性和安全性，在结构设计时，必须分析满载时结构的强度、刚度和稳定性。因此，正确的设计过程是给出结构的初步设计方案→运用有限元软件ANSYS Workbench仿真平台建立船舶牵引机械的整体结构有限元模型，并对其进行静力分析→获取结构在静载作用下的应力变形分布→对整体结构进行稳定性分析→根据分析结果，改进设计方案并进行优化。

文中在静力分析的基础上，对牵引机械进行稳定性求解，同时参照相关起重机设计规范，对于机构的初步设计方案进行合理性评估。

1 船舶牵引机械有限元模型的建立

1.1 牵引机械三维实体模型

船舶牵引机械的金属结构主要包括塔顶、起重臂架、平衡臂、滑轮组、绞车以及回转支承等组成。其中起重臂架上弦杆为φ168×12规格的无缝钢管，下弦杆为两根180×180×14的方管，腹杆为φ63×9规格的无缝钢管，拉索为φ25钢缆。根据设计意图及尺寸在PRO/E里建立船舶牵引机械初步的三维实体模型，如图1所示。

图1 牵引机械三维实体模型Fig.1 3D solid model of boat-haulage machine

1.2 牵引机械的有限元模型

1.2.1 建模原则及模型简化 根据起重机设计规范的规定，建立起重机结构几何模型过程中，忽略结构阻尼，不考虑非线性关系和过渡圆角［1］。为使有限元建模更加合理，结构模型化时重点关注了以下几点:模型能全面准确地反映整机结构特点;模型受力与实际结构在工作时的外载荷相同;模型的边界条件处理与牵引机械实际工作时的外部约束和部件间的衔接情况保持一致。牵引机械在有限元建模时，根据实际情况进行必要简化［2］。

1)回转支承简化:由于回转支承等实体部件相对结构整体而言几何尺寸较小，刚度大，质量集中，且实体部分局部不易失稳，在整机结构稳定性分析时将回转支承等实体部件采用质量等效处理［3］。

2)起重臂简化:起重臂根部通过销轴与回转支承相连，由于起重臂根部锁紧装置的作用，因而回转支承对起重臂的作用可用固定支座描述。起重臂与二根拉索的连接及拉索与塔顶的连接，均按固定铰支座处理［4］。

3)牵引机械附件简化:滑轮、绞车等附件由于相对整体结构而言几何尺寸小，质量集中，对整体结构进行静力和稳定性分析时，将附件等实体部件均采用等效刚体质量处理，其所受载荷以集中力方式加载于其与臂架的连接件之上。根据圣维南原理，这种处理仅影响附件作用点附近的局部应力大小及分布，对结构整体应力变化及分布无大的影响［5］。对于等截面部件，自重均按长度方向的均布载荷处理。

1.2.2 单元选择 牵引机械起重臂架实体部分采用三维实体单元SOLID186，而拉索则采用LINK180单元。由于Workbench平台不支持自主定义单元类型，通过Workbench平台中的DM模块建立线体模型并赋予截面特征参数，并在Mechanical模块中插入Command命令以实现对拉索的模拟。附件质量以Point Mass附加于臂架相关位置模拟。

1.3 边界条件的确定与载荷处理

鉴于工作时起重臂根部固定，该处设为固定约束，即线位移 Ux=0，Uy=0，Uz=0;角位移ROTx=0，ROTy=0，ROTz=0。塔顶以等效刚体质量处理，采用固定耦合的方式表示与之相连的拉索。

牵引机械所受载荷主要为自重、牵引载荷及风载荷等。为保证设计计算的可靠性与合理性，牵引机械的计算载荷选用最不利工况时的载荷组合:自重为分布力;牵引载荷以厂家提供数值施加;风载以分布力的形式作用于塔机侧面，其数值一般按六级风压设定，计算风压 Pw2=250 Pa［6］。

1.4 有限元模型的建立

将PRO/E中建立的三维实体模型通过相关接口导入到ANSYS Workbench平台，根据现行规范及上述处理建立有限元模型。按杆件材料规格型号和不同的截面划分单元网格。结构材料特性如表1所示。

表1 材料特性Tab.1 Material properties

起重臂的网格划分以六面体单元为主，辅以一定数量四面体及楔形单元。杆件之间连接定义为Bonded接触以模拟焊接，销钉件和与之相连部件之间的连接定义为Frictionless接触。结构阻尼忽略不计，最终得到整机有限元模型如图2所示(滑轮、绞车等部件均已按前文所述简化原则作等效处理)，共2 125 295节点，372 435单元。

图2 结构有限元模型Fig.2 Finite element model of the structure

2 船舶牵引机械强度分析

由经典力学理论可知，结构的静力学方程［7］

其中:［K］为刚度矩阵;{x}为位移矢量;{F}为力矢量。

由弹性力学给出应变位移关系及物理关系可得

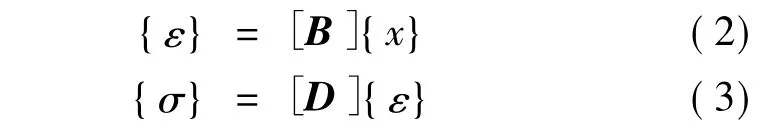
式中:［B］为应变矩阵;［D］为弹性矩阵。

通过式(1)求得结构位移，由式(2)，(3)获得相应的应力σ和应变ε数值。

设备的最大设计水平牵引载荷为20 kN，牵引缆绳与水平方向最大夹角为53°。通过对有限元模型求解，结构应力变形分布情况如图3，4所示(44倍率)。

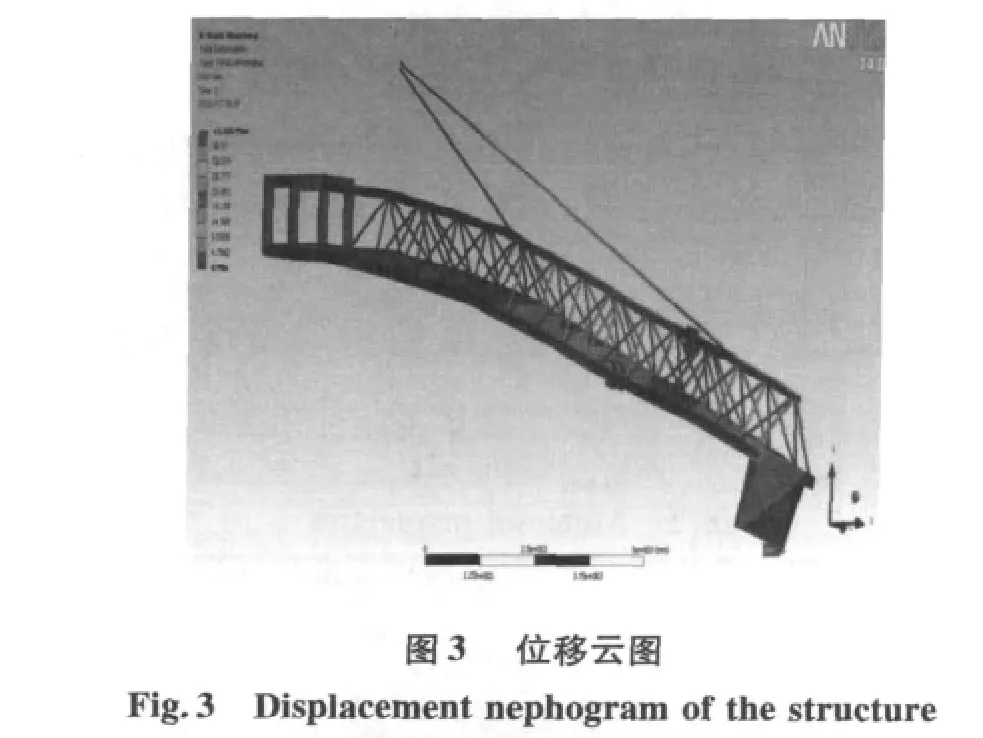
由图3，4可知，牵引机械的最大位移出现在起重臂的端部，竖向最大位移为32.36 mm，总体最大位移为43.166 mm。牵引机械的变形主要来自牵引荷载，由于横向风载作用，机身同时伴随横向弯曲，另外因牵引载荷中存在横向分力，起重臂截面略有扭转变形。

整机最大应力出现在起重臂根部附近，即与回转支承衔接处，Von Mises最大等效应力为179.27 MPa。此外，拉索吊点附近及牵引载荷一侧的下弦杆上，也有较大应力分布。

分析结果表明，最大应力值小于材料许用拉应力［σ］=345 MPa和许用压应力［σ］=510 MPa。最大变形小于《起重机设计手册》所规定的刚度要求，即吊臂悬臂挠度f≤4L/1 000。其中L为起重臂轴向尺寸，本结构设计值L=22.04 m，可见初步设计方案满足结构强度和刚度要求。

3 船舶牵引机械稳定性分析

结构的失稳破坏一般可分为平衡状态分枝型失稳和极值点失稳两种，当载荷达到一定数值时结构发生平衡状态分枝型失稳，失稳的临界载荷可以通过分枝平衡状态的分析进行计算。ANSYS程序提供了特征值屈曲和非线性屈曲两种分析方法，按照起重机设计规范，文中选择特征值屈曲对牵引机进行稳定性分析［8］。

线性屈曲分析基于经典的特征值问题，为了引出特征值问题，首先求解线弹性前屈曲载荷状态的载荷-位移关系:

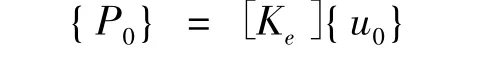
即给定{P0}，求解上式中的位移{u0}，同时可得应力{σ}。

假设前屈曲位移很小，在任意状态下({P}，{u}，{σ})增量平衡方程由下式给出:

式中:［Ke］为弹性刚度矩阵;［KG(σ)］为某应力状态{σ}下计算的几何刚度矩阵。几何刚度矩阵表示结构在变形状态下的刚度变化，与施加的荷载有直接关系。任意构件受压力时，刚度有减小倾向;反之，受拉力时，刚度有增大倾向。对三维实体单元几何刚度矩阵

其中

式中，Ni为第 i节点的形函数［9］。

假设前屈曲行为是一个外加载荷{P0}的线性函数

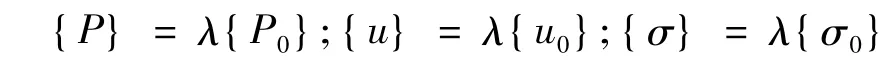
则可得

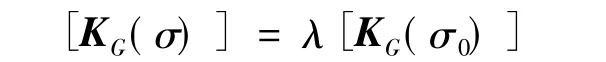
而式(4)变为

在不稳定开始时(屈曲载荷Pcr)，{ΔP}=0，存在非零位移增量{Δu}，故此时增量平衡方程变为

上述关系代表经典特征值问题，若结构处于不稳定状态，平衡方程必有特殊解，即

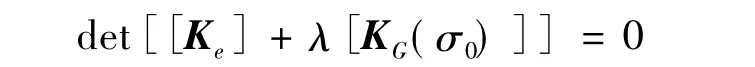
在n自由度的有限元模型中，上述方程产生λ(特征值)的n阶多项式，特征向量{Δu}n表示屈曲时叠加到系统上的变形，由计算出的λ最小值给定弹性临界载荷{Pcr}=λ{P0}。

依据上述原理，在静力分析的基础上，将相关数据传递到线性屈曲模块(Linear Buckling)，设置提取一阶屈曲模态并求解。屈曲变形结果如图5(2.2×109倍率)所示，载荷系数为26.366，实际载荷值34.3 kN，小于临界载荷值904.3 kN，牵引机械满足稳定性要求。

图5 屈曲变形Fig.5 Buckling deformation of boat-haulage machine

4 结语

基于三维建模软件PRO/E及有限软件ANSYS Workbench平台的无缝协同建模，高效率的建立了牵引机械的有限元模型，并对牵引机械的变形、各部分的应力及结构稳定性进行了全面分析，直观得到机械的应力和变形分布及失稳位置，验证了初步设计方案的合理性，也为机械的进一步优化打下了基础，充分体现了这种分析思路在现代设计中的重要价值。

［1］《起重机设计手册》编写组.起重机设计手册［M］.北京:机械工业出版社，1980.

［2］陈玮璋，顾迪民.起重机械金属结构［M］.北京:人民交通出版社，1985:7-56，216-240.

［3］杨长骥.起重机械［M］.北京:机械工业出版社，1982:1-11，42-59，371-376.

［4］于兰峰.塔式起重机结构刚性及动态优化研究［D］.成都:西南交通大学，2007.

［5］王仿，高顶.塔式起重机整体结构的有限元分析［J］.煤矿机械，2009，30(2):43-46.

WANG Fang，GAO Ding.Static finite element analysis of whole structure of tower crane［J］.Coalmine Machinery，2009，30(2):43-46.(in Chinese)

［6］张青，刘青峰，王玉玲，等.基于三维实体模型的塔式起重机钢结构设计［J］.起重运输机械，2006(7):27-29.

ZHANG Qing，LIU Qing-feng，WANG Yu-ling，et al.Design of tower crane steel structure based on 3D solid model［J］.Hoisting and Conveying Machinery，2006(7):27-29.(in Chinese)

［7］蒲广义.ANSYS Workbench 12基础教程与实例详解［M］.北京:中国水利水电出版社，2010:65-70，178-193.

［8］郑夕健，谢正义，张国忠.基于ANSYS的塔式起重机结构稳定性分析［J］.建筑机械，2007(11):76-78.

ZHEN Xi-jian，XIE Zheng-yi，ZHANG Guo-zhong.The stability of the tower crane based on ANSYS［J］.Construction Machinery，2007(11):76-78.(in Chinese)

［9］Peter Kohnke.ANSYS Inc Theory［M］.Canonsburg:ANSYS Inc.，2011:68-74.