室温下不同偏压与掺杂浓度对非对称量子阱隧穿系数的影响
2013-08-16赵瑞娟安盼龙许丽萍
赵瑞娟, 安盼龙, 许丽萍, 杨 艳
(1.中北大学电子测试技术国家重点实验室,山西太原030051;2.中北大学仪器科学与动态测试教育部重点实验室,山西 太原030051;3.中北大学理学院,山西 太原030051)
近十几年,国内外关于对称双势垒共振隧穿结构的研究已经比较成熟,报道较多[1-4],但两个及以上多个非对称势垒的研究,实验和理论较少。理论预测非对称多势垒构成的不同阱宽、垒宽的共振隧穿,理论上可导致更大的隧穿电流和峰谷比,具有设计高频量子器件等优势[5]。非对称双势阱三势垒结构,起初阱中电子的量子化能级并没有对齐,当电场方向由窄阱指向宽阱,错开的两阱的量子化能级可以处于同一高度,形成量子隧道,构成比双势垒对称结构更大的隧穿电流;而当电场反向时,两个量子阱量子化能级高度差增大,此时隧穿电流小到可以忽略不计,由此可以设计效果很好的非对称量子器件、量子开关等[6]。
1 建立基本模型
选用GaAs为势阱材料,势垒材料选用匹配AlxGa1-xAs,x=0.3,T=300 K,B 为势垒,W 为势阱。B1、B2、B3分别为 5 nm、6 nm、10 nm,W1、W2分别为4 nm、9 nm。
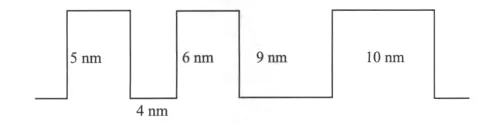
图1 非对称三势垒模型Fig.1 Asymmetric three-barrier model
2 理论推导
量子隧穿问题实际为求解一维定态薛定谔方程[7-10],下面使用传递矩阵方法求解。
多势垒结构图简化分为3个区,选z方向为纵向且垂直势垒。
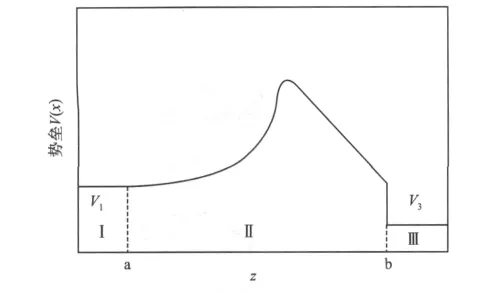
图2 任意非对称势垒曲线Fig.2 Curve of arbitrary shape barrier
则多势垒结构中电子满足薛定谔方程
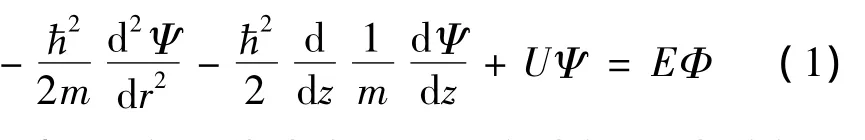
式(1)中,m和U代表有效质量和势能,E为总能。令波函数Ψ为
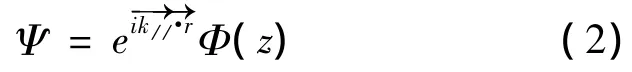
式(1)代入式(2)可得
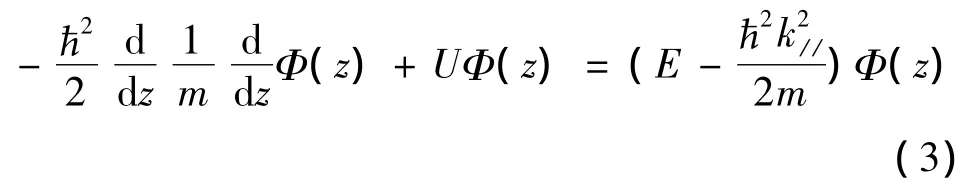
式(3)中,电子横向动能E//为

电子的总能量
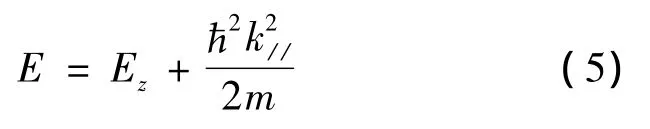
据电子总能量守恒,有
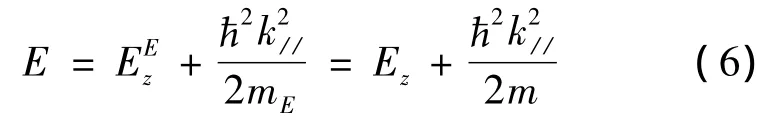
式(6)中 mE分别为发射区电子质量、总动能。
式(6)代入式(3)得

设1、2、3区的波函数Φ(z)分别为:
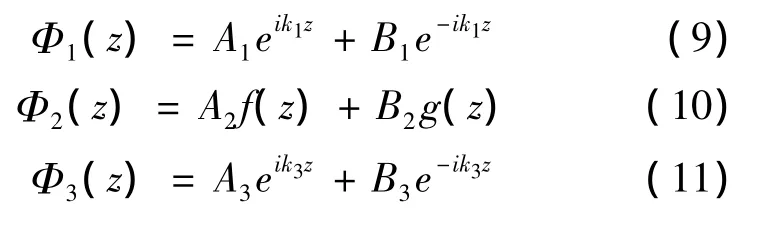
以上式中
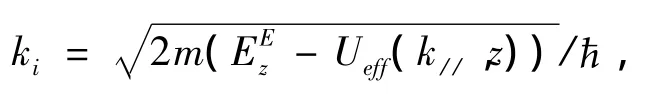
Ai和Bi分别为入射波振幅和反射波的振幅;m、EEz分别为电子有效质量、能量,Ueff(k//,z)=Vi为势垒高度。设势垒高度、宽度分别为V0、Lb,势阱宽度为LW,则透射系数Tn为
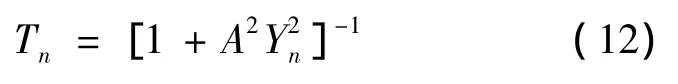
式(12)中
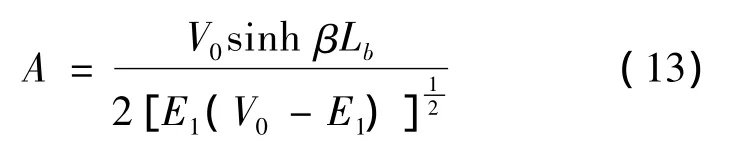
Yn为迭代函数。波函数及导数边界连续,可得Ai+1,Bi+1与Ai和Bi有
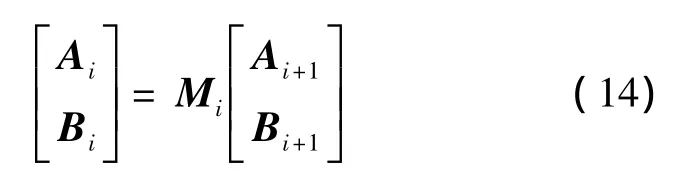
式(14)中
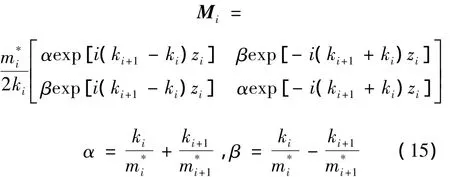
显然,式(12)为递推公式,可求得
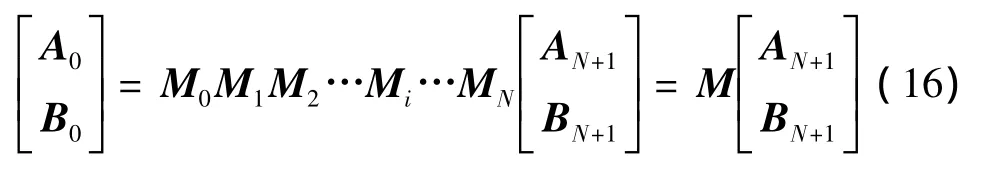
N+1个2×2矩阵乘积得M=M0M1…Mi…MN为传递矩阵。这样,就可以得到穿过任意势垒UX的透射系数近似值为
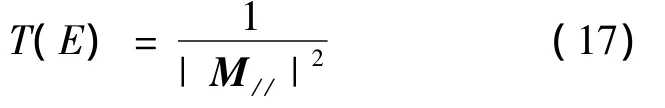
任意势垒的隧穿实际仍为解决单势垒的隧穿问题。
3 室温条件不同偏压浓度下所对应的不同隧穿系数曲线图
以下给出外加偏压1~4 V,掺杂浓度为(1017~1020)/cm3所对应的不同隧穿系数模拟曲线图。
3.1 外加偏压1 V,掺杂浓度为(1017~1020)/cm3
如图3所示。
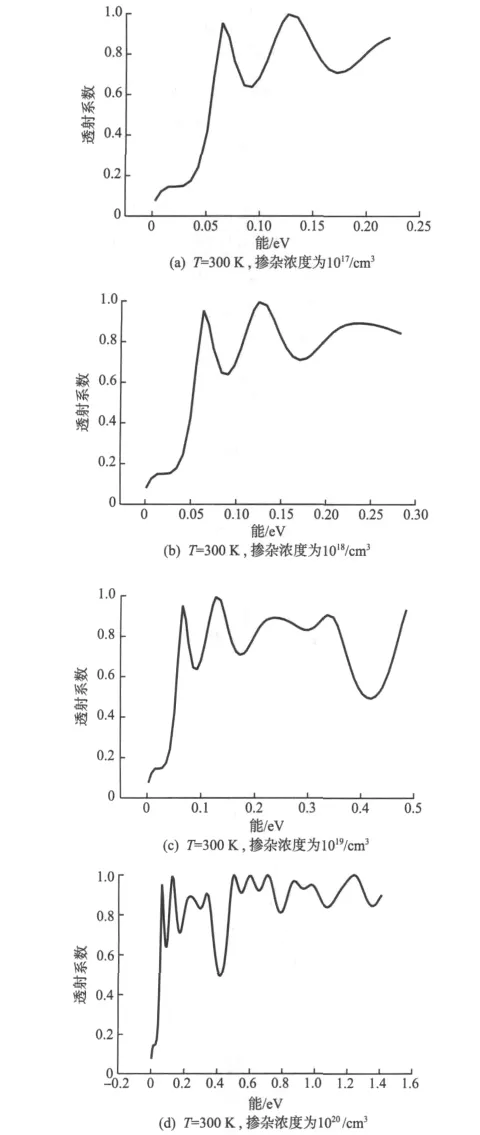
图3 T=300 K,偏压为1 V时,不同掺杂浓度对透射系数的影响曲线Fig.3 T=300 K,Bias is equal to 1 V,Transmission coefficient curves with different doping
3.2 外加偏压2 V,掺杂浓度为(1017~1020)/cm3
如图4所示。
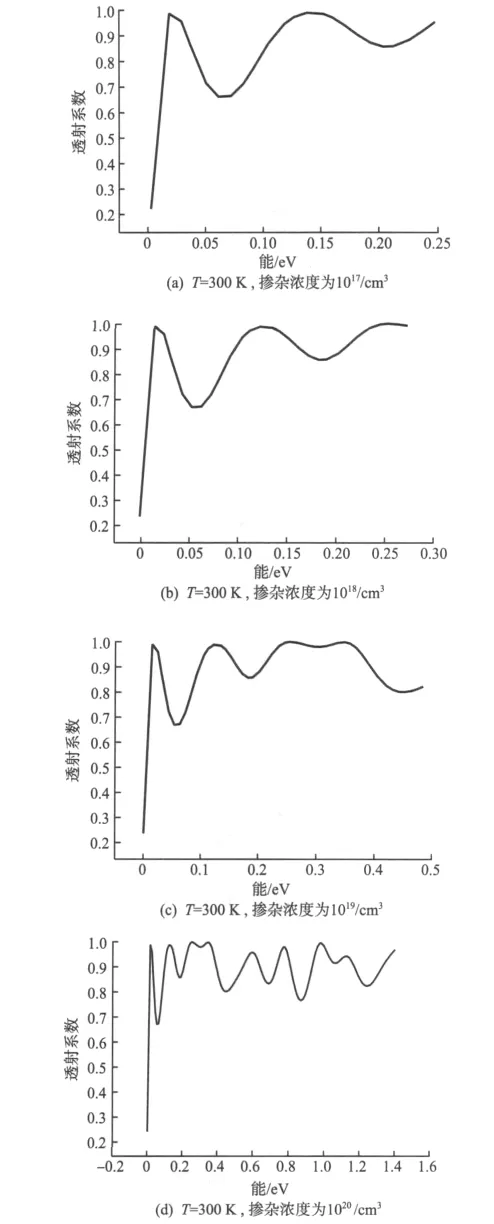
图4 T=300 K,偏压为2 V时,不同掺杂浓度对透射系数的影响曲线Fig.4 T=300 K,Bias is equal to 2 V,Transmission coefficient curves with different doping
3.3 外加偏压3 V,掺杂浓度为(1017~1020)/cm3
如图5所示。
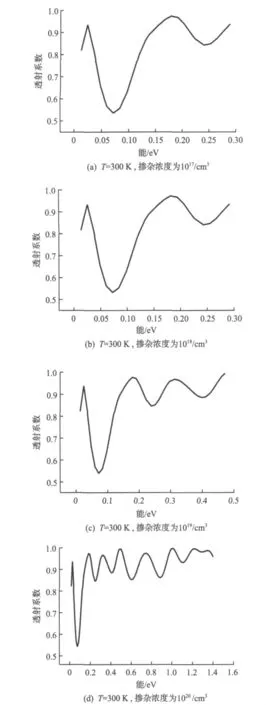
图5 T=300 K,偏压为3 V时,不同掺杂浓度对透射系数的影响曲线Fig.5 T=300 K,Bias is equal to 3 V,Transmission coefficient curves with different doping
3.4 外加偏压4 V,掺杂浓度为(1017~1020)/cm3
如图6所示。
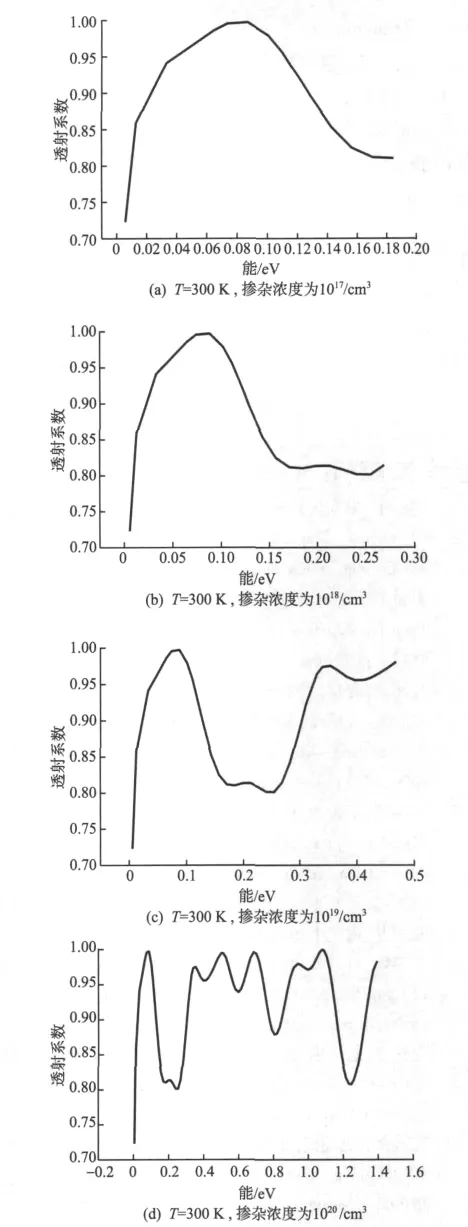
图6 T=300 K,偏压为4 V时,不同掺杂浓度对透射系数的影响曲线Fig.6 T = 300 K, Biasis equalto 4 V,Transmission coefficient curves with different doping
4 模拟结果分析
以上通过对1~4 V外加偏压下,半导体材料发射区和集电区掺杂浓度分别为1017~1020/cm3的T—E(Transmission coefficient—Energy)曲线比较。偏压小于3 V,掺杂浓度小于1020/cm3时,T—E曲线峰谷比较好;任何偏压下一旦掺杂浓度大于1020/cm3时,T—E曲线失真明显。可见制造量子器件时掺杂浓度不是越大越好,掺杂浓度控制在1018/cm3和1019/cm3两个值较合适。
5 结语
据以上模拟,针对器件室温保持不变,加置不同偏压(1~4 V偏压),不同掺杂浓度(1017~1020/cm3)下非对称纳结构量子阱透射系数的研究,发现偏压3 V以下,由于掺杂浓度所造成的半导体器件内建电场形成的影响较小[7-11],适合隧穿条件。具体的量子器件需要的掺杂浓度、温度,以及偏压条件,必须考虑内建电场对其产生的影响而对隧穿过程进行调制。得到了内建电场变化实际,从侧面反映了非平衡载流子对掺杂浓度的影响。平衡条件下载流子由于材料自身特点受到外界电场、磁场、温度、极化、压电诸多因素的影响[12],在其内部发生了随机动态漂移,材料表面形成诸多因素的空间电荷,内建电场随之形成,会使材料的非平衡态又逐渐趋于相对稳定的动态平衡态,材料的费米能级在能级图上也会达到新的平衡高度。
[1]虞丽生.半导体异质结物理[M].北京:科学出版社 ,2006:112-147.
[2]XU Li-ping.The resonant tunneling in Si1-xGex/Si superlattices[J].Solid State Phenomena,2006,42:2721.
[3]XU Li-ping,WEN Ting-dun,YANG Xiao-feng.Mesopiezoresistive effects in double-barrier resonant tunneling structures[J].Appl Phys Lett,2008,92:043-508.
[4]Jogai B,WANG K L.Dependence of tnuneling current on structural variations of superiattice devices[J].Appl Phys Lett,1985,46(2):167-168.
[5]杜磊,庄弈琪.纳米电子学[M].北京:电子工业出版社,2004.
[6]安盼龙,许丽萍,温银萍.Zn1-xCdxSe/ZnS量子阱材料的共振遂穿特性研究[J].红外,2009,30(3):35-38.AN Pan-long,XU Li-ping,WEN Yin-ping.Study on resonant tunneling effects in Zn1-xCdxSe/ZnS quantum well[J].Infrared,2009,30(3):35-38.(in Chinese)
[7]赵瑞娟,安盼龙,许丽萍,等.不同偏压温度下非对称三势垒透射系数的模拟计算[J].半导体光电,2012,33(4):540-543.ZHAO Rui-juan,AN Pan-long,XU Li-ping,et al.Simulations on asymmetric three-barrier transmission coefficients under different bias and temperatures[J].Semiconductor Optoelectronics,2012,33(4):540-543.(in Chinese)
[8]王辉.静压对Ⅲ—Ⅴ族量子阱共振隧穿的影响[D].太原:中北大学,2007.
[9]安盼龙.内建电场对纳结构半导体材料功函数调制研究[D].太原:中北大学,2009.
[10]李春雷,肖景林.势垒的非对称性对隧穿几率的影响[J].内蒙古民族大学学报,2006,21(3):253-256.LI Chun-lei,XIAO Jing-lin.The effect of asymmetric barriers on tunneling probability[J].Journal of Inner Mongolia University for Nationalities,2006,21(3):253-256.(in Chinese)
[11]安盼龙,赵瑞娟,许丽萍.内建电场对纳构半导体功函数的调制[J].武汉工程大学学报,2011,33(4):50-53.AN Pan-long,ZHAO Rui-juan,XU Li-ping.Modulation on work function of nano semiconductor materialby builtin electric field[J].J Wuhan Inst Tech,2011,33(4):50-53.(in Chinese)
[12]安盼龙,赵瑞娟.小偏压下阱中阱结构的量子隧穿特性及其实现[J].量子电子学报,2011,28(5):629-634.AN Pan-long,ZHAO Rui-juan.Quantum tunneling properties and realization in low-biased well of wells structures[J].Chinese Journal of Quantum Electronics,2011,28(5):629-634.(in Chinese)
