基于中间均衡直方图的红外图像非均匀性校正

康长青，张其林，郑 毅，刘雨潇

(湖北文理学院数学与计算机科学学院，湖北襄阳441053)

1 引言

红外焦平面阵列的像元响应不一致引起的非均匀性问题［1］，已经严重影响红外探测器的成像性能，因此在实际应用中必须进行非均匀性校正。目前已有的校正算法主要有参考源校正法［2］和场景校正法［3－9］两大类。前一类算法的主要缺点是需要中断系统的正常工作，不便于实时校正。而后一类算法直接利用场景信息，不需要参考辐射源，不影响系统的正常工作，已成为目前研究的主要方向。由于大多数场景校正算法需要一段较长时间的场景变化，因而存在运算量大，收敛速度慢，校正性能不高的缺点。

文献［3］提出的基于恒定统计约束的校正算法和文献［4］提出的基于神经网络的校正算法，由于计算量小，存储代价低，得到了广泛的关注。针对这两种方法存在着鬼影(ghosting artifact)问题，文献［5］和［6］分别提出了运动阈值去鬼影和时域统计去鬼影的恒定统计改进算法，但是存在着受场景随机噪声影响的不足。文献［7］和文献［8］分别提出了自适应学习率和门限自适应学习率的神经网络改进算法，然而仅在一定程度上只是减缓了鬼影的出现，并不能有效地消除鬼影。针对以上算法的不足，本文将场景校正的算法思想，运用到单幅图像的行或列上，提出基于中间直方图均衡非均匀性校正算法，来达到消除鬼影的目的。

2 中间均衡直方图

在非均匀性校正算法研究中，可以将红外焦平面像元响应近似为线性模型，即:

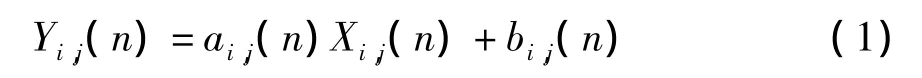
其中，Yi，j(n)是带有非均匀性的成像器输出图像;Xi，j(n)是真实的输入图像;ai，j(n)和 bi，j(n)是(i，j)像元响应的增益和偏置系数。非均匀性校正算法的目标是从 Yi，j(n)中求解 ai，j(n)和 Xi，j(n)。

为了校正不同红外相机间的增益偏差，通过对比同一场景不同图像，文献［10］提出了中间直方图的均衡算法。

设H0，H1分别是两幅灰度图像U0，U1的累积直方图，为了映射一幅所需的直方图，若采用直接平均的均衡化方法(如H=(H0+H1)/2)可能会增加背景噪声的对比度而降低有用信号的对比度，因此文献［10］提出了中间直方图均衡算法(原理如图1所示)，其直方图变化公式如下:

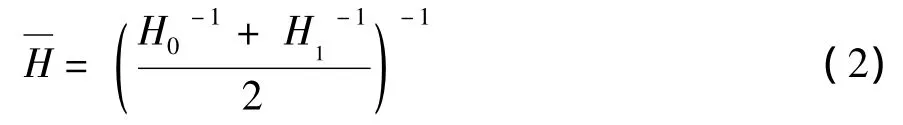
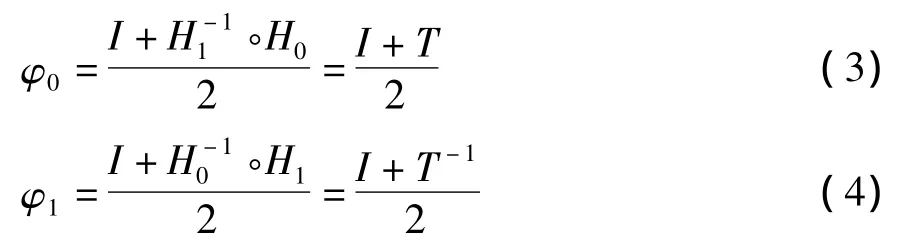
其中，H=((I+T/2))－1。H=((I+T－1/2))－1。H，

01I为恒等映射，从以上公式可知，映射T将U0的直方图映射为H1，φ0和φ1的具体求解参考文献［10］。

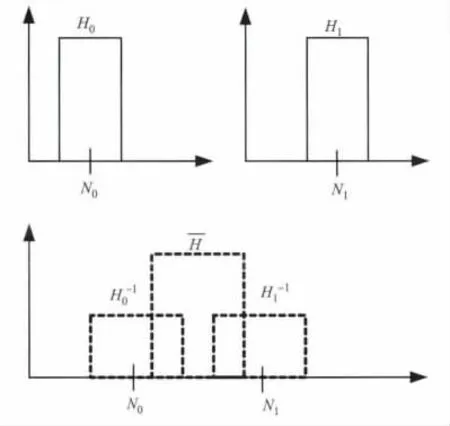
图1 中间均衡直方图原理

3 基于中间直方图的非均匀校正

目前基于统计的非均匀性校正算法一般在场景变化中采用每个传感器像素的时序直方图进行直接平均的方式。从文献［10］可知，中间直方图能够取得比直接平均更好的均衡效果，因此将场景校正的算法思想，运用到单幅图像的行或列上。由于单幅图像的一列(或一行)包含了足够的直方图信息，加上连续成像，两个相邻列的变化非常小，因此可以将这两列的直方图看作近似相等。本文算法采用将图像中每一列的直方图，运用中间直方图算法映射到相邻的两行，得到算法的处理流程如下:

(1)设长宽为N×M的8位灰度图像U(x，y)，计算图像每一列ci的累积直方图Hi:

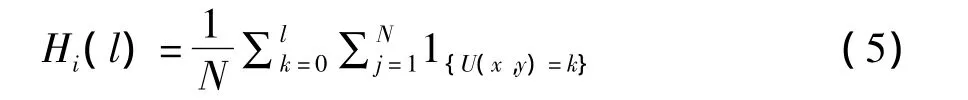
(2)计算ci的局部中间直方图:

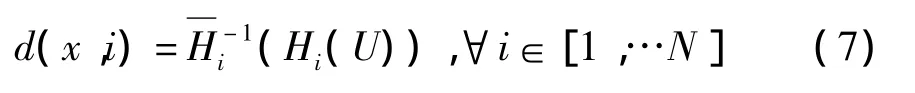
标准偏差σ的选择，可以从一个小的参数开始逐渐增加，直到处理的图像Uσ达到较好的视觉质量为止，即:

4 实验结果与讨论

为了验证本文提出算法的非均匀性校正能力，并与文献［11］提出的总变差(TV)校正算法进行对比，利用带有未制冷IRFPA探测器的Thermal CAM P65红外相机，关闭“Noise Reduction”和“Shutter Period”选项，获取一系列非均匀条纹的源图像(raw images)，在Windows XP下，利用MATLAB软件进行仿真实验。

图2给出了算法的实验效果图。从图2(a)可以看出，原始图像含有竖状条纹噪声和其他随机噪声。图2(b)是经过TV算法处理后的效果图，从中可以看出部分条纹未能有效的去除，且算法过度平滑，造成了阶梯效应，影响了图像的主观视觉质量。图2(c)是本文算法的处理效果图，可以看出，算法校正了原始图像中的绝大部分条纹噪声，没有造成图像细节特征的模糊，图像的细节特征得到较好的保护，主观图像质量较高。

图2 算法效果图

采用行列均值作为算法的评价指标，得到图2的三个处理图像的像素均值(Pixel Mean)分别如图3和图4所示，从图中可以看出，TV算法和原始图像的均值较为接近，由于条纹噪声的影响，均值都较大，而本文算法的行列均值都小于原始图像和TV算法，取得了较好的校正效果。

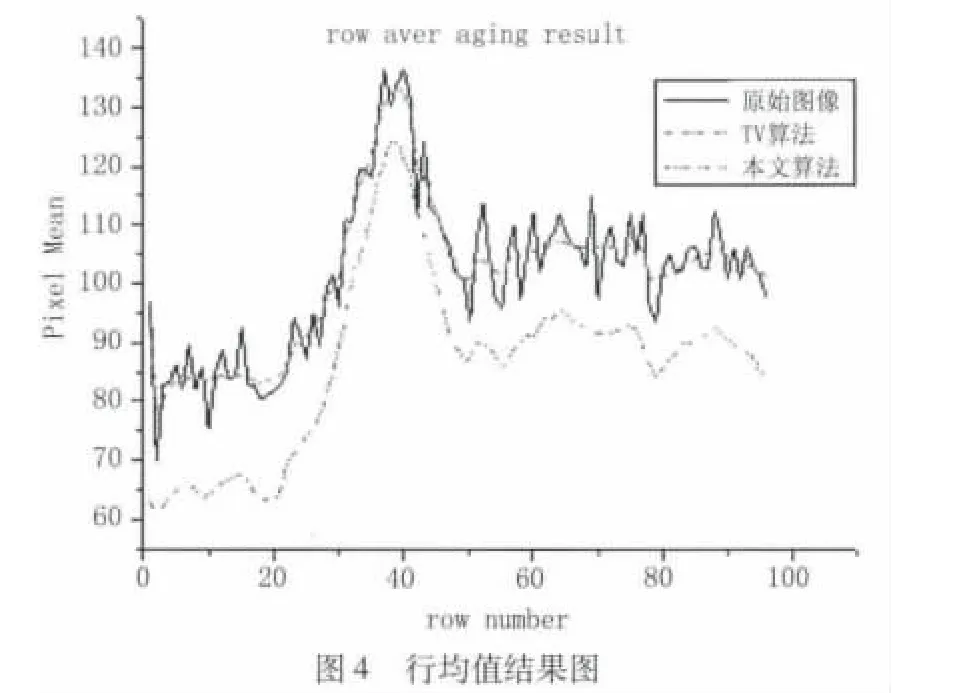
对于行状非均匀性噪声，本文算法仍然可以取得和上面类型的效果。由于本文算法在单幅图像上进行，避免了“鬼影”和参数校正随时间漂移;并且从主观视觉质量和均值来看，算法的校正能力优于TV算法。

5 结束语

本文提出了一种针对单幅红外图像的非均匀性校正模型，建立了图像各列中间均衡直方图算法来替代原始列的直方图数的校正策略。实验表明，算法简单快捷，易于工程实现，不仅避免已有算法的鬼影和参数时间漂移问题，而且具有较好的图像视觉质量。算法的不足之处在于仅针对行列状条纹噪声，没有对其他噪声进行集成处理，这将是作者下一步的努力方向。

［1］ Milton A F，Barone F R，Kruer M R.Influence of nonuniformity on infrared focal plane array performance［J］.Optical Engineering，1985，24(5):855 －862.

［2］ Friedenberg A，Goldbatt I.Nonuniformity two-point linear correction errors in infrared focal plane arrays［J］.Optical Engineering，1998，37(4):1251 －1253.

［3］ Harris J G，Chiang Y.Nonuniformity correction of infrared image sequences using the constant statistics constraint［J］.IEEE Trans. ImageProcess，1999，8(8):1148－1151.

［4］ Scribner D A，Sarkady K A，Kruer M R，et al.Adaptive retina-likepreprocessing forimagingdetectorarrays［J］//Proc.of IEEE Int.Conf.on Neural Networks，1993，3:1955 －1960.

［5］ Harris J G，Chiang Y.Minimizing the ghosting artifact in scene-based nonuniformity correction［C］//Proc of SPIE，1998，3377:106 －113.

［6］ Rossi A，Diani M，Corsini G.Temporal statistics de-ghosting for adaptive non-uniformity correction in infrared focal plane arrays［J］.IET Electron.Lett.，2010，46(5):348－349.

［7］ Vera E，Torres S.Ghosting reduction in adaptive nonuniformity correction of infrared focal-plane array image sequences［C］//Proc.of IEEE Int.Conf.Image Process，2003，3:II－1001 －4.

［8］ Hardie RC，BaxleyF，Brys B，et al.Scene-based nonuniformity correction with reduced ghosting using a gated LMS algorithm［J］.Opt.Express，2009，17(17):14918 －14933.

［9］ Ji Eryou，Gu Guohua，Chen Qian，et al.Dual channel constant statistic NUC algorithm of separate band［J］.Laser＆ Infrared，2011，41(4):474 －478(in Chinese)季尔优，顾国华，陈钱，等.双通道分频段恒定统计非均匀性校正算法［J］.激光与红外，2011，41(4):474 －478.

［10］ Delon J.Midway image equalization［J］.Journal of Mathematical Imaging and Vision，2004，21(2):119 －134.

［11］ Gilboa G，Sochen N，Zeevi Y Y.Texture preserving variational denoising using an adaptive fidelity term［C］//Proc.of VLSM，2003:137 －144.