基于二维经验模态分解的高光谱影像去噪方法

厉 祥，王文波

(武汉科技大学理学院，湖北武汉430065)

1 引言

高光谱遥感影像具有很高的空间分辨率，而且可以为图像中的每个像元提供高达数百个波段的光谱信息，包括可见光、红外和紫外等区域。因此，高光谱遥感图像具有图谱合一的特点，该特点使得很多在常规遥感中不能识别的地物，在高光谱遥感图像中可以得到有效的识别［1］。当前，高光谱遥感图像在军事监测、大气和农业监控等多个领域都得到了越来越广泛的应用［2－4］。高光谱图像在获得和传输过程中，由于受到大气、电磁辐射等较多复杂因素的干扰，会产生大量的噪声，从而降低图像数据的可靠性、影响图像的后继分析处理，因此对高光谱遥感图像进行去噪对于光谱影像的后续处理非常有必要［5］。

小波分析由于其良好的时频分析特性在高光谱图像去噪中得到了大量的应用［5－7］，但利用小波变换对高光谱图像进行去噪时需要预先给定小波基和分解层数［8］。相同条件下，采用不同的小波基函数和分解层数，对去噪结果影响很大，这给利用小波变换进行高光谱图像去噪带来了很大的不便［9］。近年来，经验模态分解(empirical mode decomposition，EMD)算法被逐渐应用到了遥感图像的去噪中，取得了很好的去噪效果［10－11］。EMD是一种新颖的多尺度时频分析方法，该方法将信号分解成有限个固有模态函数(intrinsic mode function)与一个趋势函数之和，特别适合非线性、非稳态信号的处理［12］。EMD分解不需要预先给定基底和分解层数，在分解过程中其根据信号自身的特性，自适应地通过迭代产生基地并确定最优分解层数，在一定程度上克服了小波变换的不足。研究表明，对于非线性和非稳态信号，EMD分解比小波分解具有更好的空间和频率特性［12－13］。

一维经验模态分解优良的分解特性可以拓展到对二维图像信号的分解中［14］，本文将二维经验模态分解(bidimensional bemd)应用到高光谱图像的去噪中，充分考虑高光谱图像所具有的谱间强相关性和图谱合一的特点，提出了一种基于二维经验模态分解的高光谱图像去噪方法。该方法中首先利用二维经验模态分解对高光谱各波段图像分别进行分解;然后根据含噪声较大的波段与含噪声较小的波段间的波长对应关系，对含噪声较小的波段的固有模态函数系数进行相应的加权求和;以加权求和后的imf系数代替噪声较大的波段的imf系数;最后对处理后的各层imf系数进行累加求和得到去噪后的高光谱图像。通过AVIRIS实验数据对该算法的有效性进行了验证，实验结果表明:与经典的高光谱图像去噪算法相比，本文方法能更有效地去处高光谱图像中的噪声，并能更好地保留图像的细节信息。

2 二维经验模态分解

二维经验模态分解(BEMD)可以将高光谱图像分解成频率从高到低的有限个二维固有模态函数(BIMF)和一个余项(R)。BEMD具体的分解方法如下［14］:

1)数据初始化，令 Ires=f，Ir=f，其中 f为待分解图像，Ir表示余项;

2)求Ires的所有极大值点集和极小值点集;

3)分别对极大值点和极小值点进行曲面插值，得到图像的上、下包络面，根据上下包络面求出图像的均值EM;

4)抽取细节，令Ires=Ires－EM;

5)重复步骤2－4，直到 Ires是一个固有模态函数;

6)令 Ir=Ir－Ires，Ires=Ir;

7)重复步骤2－6，直到达到分解层数或Ir的极值点个数少于2。

经过第K层BEMD分解后，原始图像可以被表示为:

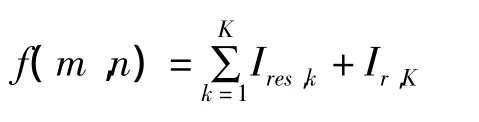
其中，Ires，k是第k个二维固有模态函数;Ir，K是经过K层分解后的趋势图像。在BEMD的分解算法中，极值点选取、包络曲面的插值算法和内蕴模式函数BIMF的筛选终止条件是算法的核心内容。考虑到高光谱遥感图像尺寸较大且极值点很多，本文中采用8－邻域极值选取的方法来抽取图像的极值点;采用Delaunay三角剖分的方法进行包络曲面插值;采用标准差判断条件作为筛选过程停止的标准。

3 高光谱影像特征分析

高光谱遥感图像数据是一种三维图像数据，其数据由二维图像加一维光谱信息构成。二维图像用来展现地表被拍摄物体的空间信息特征，而一维光谱信息则用来描述图像中每一像元处的光谱特征，从而实现遥感数据空间信息与光谱信息的有机融合［1］。由文献［15］可知，高光谱图像中每个波段噪声的方差随着光谱波长的变化而变化，有些波段会含有较大的噪声，而有些波段所含的噪声则较小，并且某些波段的噪声会非常小，几乎可以认为其不含噪声。由于高光谱数据具有密切的谱间相关性，因此各波段的图像经二维经验模态分解后其高频固有模态函数的系数具有相似的轮廓曲线，而且如果两幅图像的波段越接近，则其高频固有模态函数间的系数也将会越接近。因此在对含噪声较大的波段进行去噪时，可以利用含噪声较小波段的高频固有模态函数系数进行辅助去噪，此即为本文去噪的主要的思想。

图1 海洋油膜高光谱图像Fig.1 Hyper-spectral image of oil spill

图1是一幅海洋溢油油膜区的高光谱影像，油膜区影像信息主要包括油膜和海水面，以及以条带噪声为主的多种噪声。通过分析不同频率的高光谱影像的光谱曲线(图2所示)，可以看出光谱曲线因噪声的影响而呈现不规则锯齿状分布，有些波段噪声较大，而有些则噪声较小，甚至有些波段可以认为没有噪声是纯信号［15］。高光谱图像经二维经验模态分解后，噪声基本都集中在高频bimf中，因此根据不同波段间的波长对应关系，利用含噪声较小波段的高频bimf系数代替含噪声较大波段的高频bimf系数，可以有效去除高光谱图像中含噪波段的噪声。

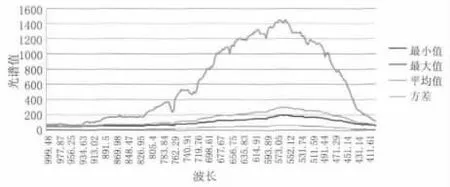
图2 海洋油膜高光谱图像频谱信息Fig.2 Spectrum information of hyper－spectral image of oil spill

4 基于二维经验模态分解的高光谱图像权系数去噪法

由于高光谱图像具有明显的谱间相关性［6，15］，图像波段相邻越近，其二维经验模态变换的高频bimf系数幅值大小亦越接近，本文提出的权系数去噪法即是通过受噪声污染小的波段的高频系数辅助噪声污染大的波段进行去噪，权重值通过不同谱间波段相邻距离的远近(即谱间相似性的大小)进行相应的确定。

通过二维经验模态分解可以获得图像的一组bimf系数和一个余项系数。首先，分别对参考图像(噪声较小的波段图像)和噪声图像(噪声较大的波段图像)进行BEMD分解，得到不同频率的bimf系数和余项系数，其中余项系数包含了该波段的大部分能量，保持余项系数不变，也就能够保持该波段中大部分光谱信息不变。而高频的bimf系数表示信号的奇异信息，对含噪声小的波段图像(参考图像)而言，高频系数反映该波段图像的轮廓信息;对噪声图像而言，高频系数既包含该波段的轮廓信息，又包含噪声信号。因此对相邻近的参考波段的高频bimf系数进行加权求和，不仅可以得到含噪波段的高频系数的近似值，还可以恢复被噪声破坏的轮廓信息，从而有效地去除含噪较大的波段的噪声，并较好地保留图像的细节信息。

设λn为波段n的波长，参考波段I0、IN位于点(l，k)的 bimf系数分别为和。则新的高频bimf系数的计算公式为:

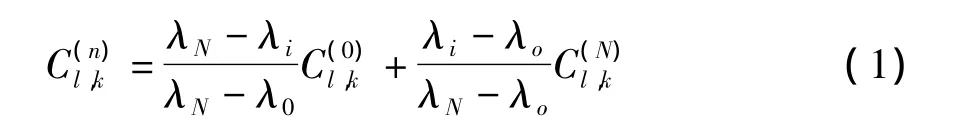
基于二维经验模态分解的高光谱图像权重系数去噪方法具体实现如下:

(1)假设待去噪的高光谱遥感图像为:In，n=1，2，…，N;

(2)对各波段图像 In，(n=1，2，…，N)进行二维经验模态分解;

(3)对n=1，2，…，N －1的各波段图像计算其新的高频bimf系数，

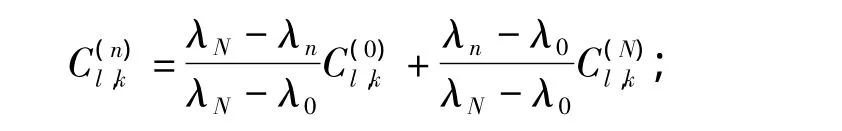
(4)当 n=1，2，…，N －1，用新计算的高频 bimf系数代替In的原始系数，再进行二维经验模态分解逆变换，得到重构后的去噪图像。

5 实验分析

实验数据采用美国喷气实验室通过红外成像光谱仪所获取的高光谱影像，波长范围在460～760 nm之间共有224个波段。选取 Jasper，Altitude和Lunar Lake三幅高光谱影像中的52～64波段的数据进行实验，截取图像大小为512×512，利用含噪声较少的52和64波段影像作为参考数据，对53～63波段的图像添加方差为40的白噪声作为噪声图像。

实验中才用信噪比和均方误差比较不同算法的去噪效果。信噪比可以较好衡量去噪后图像与原图像之间的相似程度。第n波段高光谱图像去噪后的信噪比为:

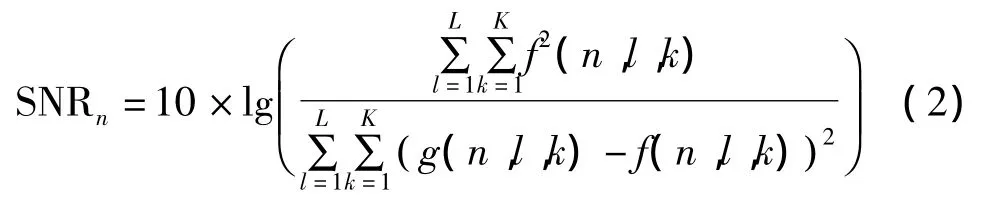
去噪后图像的均方误差定义为:

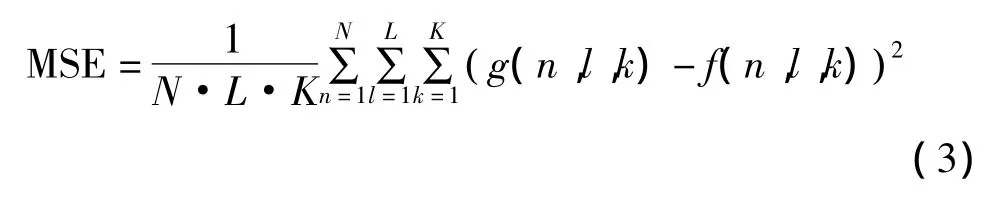
在以上两式中，f( n，l，k)表示第 n波段原始图像在点(l，k)处的像素值;g( n，l，k)表示去噪后图像在点(l，k)的像素值;L和K分别表示高光谱图像的长、宽;N表示高光谱图像总的波段数。

本文实验在matlab2011b环境下进行，对所选取的高光谱图像分别利小波域BayesShrink去噪法以及本文方法进行去噪，在利用小波进行去噪时所选用的小波基为db8，分解层数取为7。不同方法去噪后的去噪后图像的信噪比和均方误差如表1所示。从表1可以看出，本文方法去噪后的高光谱(油膜)图像数据具有较高的信噪比，且重构信号的均方差较小。与小波域BayesShrink去噪方法相比，信噪比平均提高约5.920，均方误差平均降低约4.104。实验结果表明本文方法与基于小波的去噪算法相比，能够更有效地滤除图像中的噪声，而且能够更好地保留边缘和纹理等细节信息。

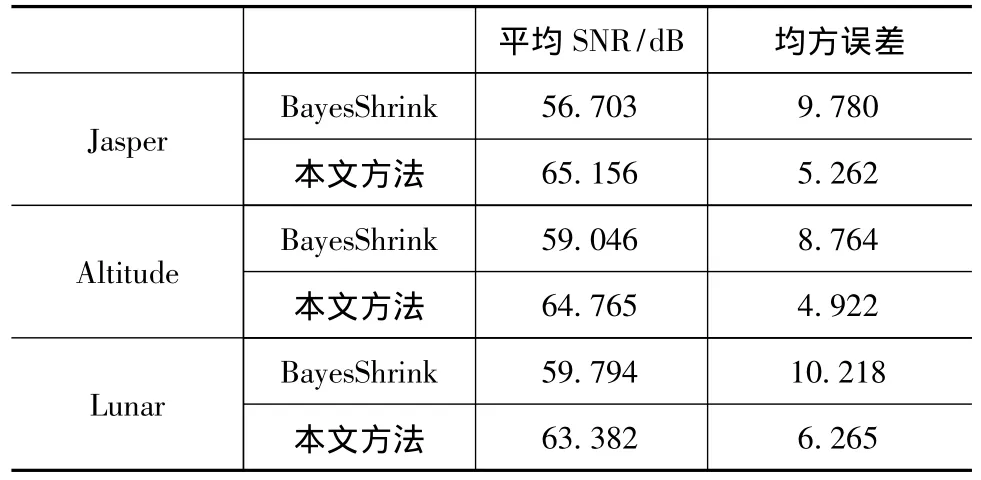
表1 不同方法去噪后的信噪比(SNR)和均方误差(MSE)

图3 第61波段高光谱影像去噪结果比较

图3分别列出了三个数据61波段的原始图像数据、噪声图像、小波BayesShrink方法去噪后图像以及本文方法去噪后图像。从视觉效果看，小波去噪算法和本文方法都能较好地抑制噪声，但小波域BayesShrink方法去噪后图像中有部分噪声斑点不能去除，去噪后图像的部分细节被模糊。本文方法对高光谱图像条带状噪声和斑点噪声都能够较好地去除，而且与小波去噪算法相比，去噪后图像具有更好的清晰度，表明本文方法在有效去除噪声的同时也较好地保留了图像中目标轮廓特征的细节信息，更有利于高光谱图像的分割、边缘提取和分类判别等后期处理。

6 结论

本文提出了一种基于二维经验模态分解和光谱特性的高光谱图像噪声消除方法。首先利用BEMD对高光谱图像进行精细分解，使噪声和信号能够更好地分离;然后利用高光谱图像的谱间相关性，采用高频bimf系数加权的方法构造去噪后波段图像高频系数，按照波段间的距离对权值进行赋值，防止单一波段的光谱信息被过多引入，同时保证在去除噪声的过程中能够较好地保持图像边缘、纹理等细节信息。

实验结果证明，基于二维经验模态分解的高光谱图像权系数去噪方法较之小波去噪方法法降噪效果有较好的提高，能够更为有效地提高图像质量，改善图像的视觉效果，为高光谱图像的进一步分析和处理提供更为可靠和有效的前期准备。

［1］ Tong Qingxi，Zhang Bin，Zheng Lanfen.Multidisciplinary applications of hyperspectral remote sensing［M］.Beijing:Electronic Industry Press，2006:6 －25.(in chinese)童庆禧，张兵，郑兰芬.高光谱遥感的多学科应用［M］.北京:电子工业出版社，2006:6－25.

［2］ Zhu Rongguang，Ma Benxue，Gao Zhenjiang，et al.Research progress in nondestructive detection of livestock product quality based on hyperspectral imaging［J］.Laser＆ Infrared，2011，41(10):1067 －1071.(in chinese)朱荣光，马本学，高振江，等.畜产品品质的高光谱图像无损检测研究进展［J］.激光与红外，2011，41(10):1067－1071.

［3］ Gao Xuhui，Qi Meng.Anomaly detection based on 3D texture segmentation for hyperspectral image［J］.Laser＆ Infrared，2012，42(5):561 －566.(in chinese)高旭辉，祁蒙.基于三维纹理分割的高光谱图像异常检测［J］.激光与红外，2012，42(5):561 －566.

［4］ Liu Yangchuan，Bayanheshig，Cui Jicheng，et al.Lossless compression of hyperspectral image based on prediction and JPEG2000［J］.Laser ＆ Infrared，2012，42(4):452 －457.(in Chinese)刘仰川，巴音贺希格，崔继承，等.基于预测与JPEG2000的高光谱图像无损压缩方法［J］.激光与红外，2012，42(4):452 －457.

［5］ Suen Lei，Gu Defeng，Luo Jianshu.Hyperspectral imagery denoising method based on wavelets［J］.Spectroscopy and Spectral Analysis，2009，29(7):1954 －1957.(in chinese)孙蕾，谷德峰，罗建书.高光谱遥感图像的小波去噪方法［J］.光谱学与光谱分析，2009，29(7):1954 －1957.

［6］ CHEN G，QIAN S E.Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage［J］.IEEE Transactions on Geoscience and Remote Sensing，2011，49(3):973 － 980.

［7］ Sun Lei.Wavelet construction theory and its applications in hyperspectral remote sensing image denoising and compression［D］.Changsha:National university of defense technology，2010.(in Chinese)孙蕾.小波构造理论及其在高光谱遥感图像去噪与压缩中的应用［D］.长沙:国防科学技术大学，2010.

［8］ Chen Xiaoxi，Wang Yanjie，Liu Lian.Deep study on wavelet threshold method for image noise removing［J］.Laser＆ Infrared，2012，42(1):105 －110.(in Chinese)陈晓曦，王延杰，刘恋.小波阈值去噪法的深入研究［J］.激光与红外，2012，42(1):105 －110.

［9］ Olufemi A，Vladimir A，Auroop R.Empirical mode decomposition technique with conditional mutual information for denoising operational sensor data［J］.IEEE Sensors Journal，2011，11(10):2565 －2575.

［10］ HAN Chunming，HUA Dong G，CHANG Lin，et al.A novel method to reduce speckle in SAR images［J］.International Journal of Remote Sensing，2002，23:5095 －5101.

［11］ Y Kopsinis，S Mclaughli.Development of EMD-based denoising methods inspired by wavelet thresholding［J］.IEEE Transactions on Signal Processing，2009，57(4):1351－1362.

［12］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proc.of the Royal Society of London，1998，A454:903 －995.

［13］ Wu Jun，Zhang Yufeng.The differences analysis on filtering properties of empirical mode decomposition and wavelet decomposition［J］.Journal of Yunnan University(Natural Sciences Edition)，2012，34(3):285 －290.(in Chinese)吴俊，张榆峰.经验模态分解和小波分解滤波特性的比较研究［J］.云南大学学报，2012，34(3):285 －290.

［14］ Zheng Youzhi，Qin zheng.Medical image fusion algorithm based on bidimensional empirical mode decomposition［J］.Journal of Software，2009，20(5):1096 － 1105.(in Chinese)郑有志，覃征.基于二维经验模态分解的医学图像融合算法［J］.软件学报，2009，20(5):1096 －1105.

［15］ Othman H，Qian S N.Noise reduction of hyperspectral imagery using hybrid spatial-spectralderivative-domain wavelet shrinkage［J］.IEEE Trans.on Geoscience and Remote Sensing，2006，44(2):397 －408.