灰色关联决策方法评价及优选复杂井型研究

2013-10-25安雷，思娜

石油地质与工程 2013年4期

安雷，思娜

（1.中国石化国际石油勘探开发有限公司，北京 100083；2.中国石化石油工程技术研究院）

随着石油工业的发展，压裂井、水平井和分支井等越来越多的复杂井型应用于各种复杂油气藏，不同井型直接影响油气田最终的经济效益。最优井型的选择应该在满足油藏、钻井、完井等条件下，对技术指标和经济指标进行综合评价［1］。选择最优井型必须进行多目标评价，但是到目前为止，对于不同井型的评价都仅限于初始产能值或钻井成本等单一的技术或经济指标［2－5］的对比，考虑不够全面，优选出的井型有时并不是最优，影响油层的有效开采。

本文基于等效井径理论，建立压降分布和井筒流动的耦合模型，基于灰色关联方案综合考虑多个评价指标，对不同井型进行评价及优选。

1 多指标综合评价模型

1.1 技术指标评价模型

1.1.1 初始产能值

本文采用半解析方法求解初始产能值。求解思路是沿井身轨迹将井筒分成若干段，基于等效井径模型，对每一段的压降分布模型和井筒流动模型耦合求解，可求得初始产能值。

以常规水平井为例。假设一常规水平井，将水平段分成n个小段，第i小段长为Li，距油层底部距离为Zw［i］，中心坐标为（x［i］，y［i］）如图1所示。

将每一水平微元段等效成一口直井，稳态时等效井径模型［6］为：

图1 水平井微元水平段示意图

其中：h——油层厚度，cm；kh——水平渗透率，10－3μm2；kv——垂直渗透率，10－3μm2；rw，i——第i水平微元段井筒半径，cm；L——水平段长度，cm；Skin——表皮系数，无因次。

运用势的叠加理论，对每口直井进行压降叠加，示意图如图2。

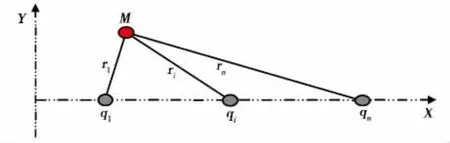
图2 水平井微元水平段压降叠加原理示意图

取各等效井井壁处的势整理后得压降分布模型：

其中：μ——原油粘度，mPa·s；B——体积系数，无因次；re——供给半径，cm；qj——第j水平微元段产量，m3／s。

中心坐标为（x［i］，y［i］）的第i微元段的井筒流动压降可以表示为［7］：

其中：ρ——流体密度，kg／m3；qws，j第j 微元段井筒壁面流入流量，m3／s；ft——水平井筒跟端摩擦系数，无因次；D——井筒直径，cm。

根据耦合压降分布模型与井筒流动模型，可得：

迭代求解上述方程组，QH＝q1＋q2＋q3＋…＋qn可求得常规水平井的初始产能值。

1.1.2 累计产油量

基于已有的生产数据，分别用阿普斯（Arps）模型、修正的胡氏模型（XH模型）及俞启泰模型（YII模型）进行拟合回归，可得三种不同的产能递减模型。针对目前以“残差平方和”作为判别依据可能会出现矛盾判别的问题，本文运用灰色关联因素分析的方法优选产能递减模型。将不同模型的动态预测数据与实际生产数据做灰色关联分析，关联度最大的预测数据为拟合结果最好，及相对应的产能递减模型为最优。

1.2 经济指标评价模型

1.2.1 钻井成本

钻井成本是指在一定时期内完钻一定数量进尺的井所支出的各种生产费用的总和。按照原石油部制定的《钻井工程成本核算和管理方法》的规定，钻井成本可主要分为以下七方面的内容［8］：新区临时工程成本；钻前工程费用；钻井工程成本；录井测试作业成本；固井工程成本；施工管理费用；完井试油工程成本。各部分可按照与时间的相关性，运用胡月亭［9］方法分别求解。

1.2.2 净现值

净现值［10］是指在基准收益率或给定折现率条件下，投资方案在寿命期内各年净现金流量值现值的代数和。

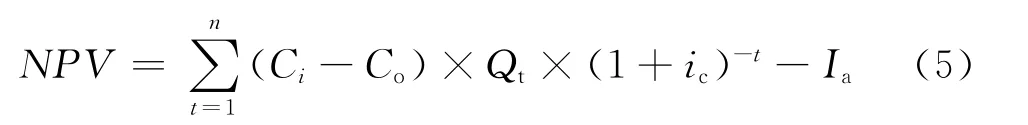
其中：t——时间，年；n——评价年限，年；Ci——油价，元／吨；Co——经营成本，元／吨；Qt——t时刻的产油量，吨／年；ic——基准收益率，无因次；Ia——投资，元。

净现值大于零，表明项目的获利能力超过了基准收益率或设定折现率的获利水平。一般来说，NPV≥0的项目是可以接受的。

2.2.3 动态投资回收期

动态投资回收期［10］是指在基准收益率或一定折现率下，投资项目用其投产后的净收益现值回收全部投资现值所需的时间，一般以“年”为单位。

将计算所得的动态投资回收期Tc与国家规定的投资回收期T′c相比较，若Tc≤T′c，项目可行；若Tc＞T′c，项目不可行。

2 实例计算与分析

以尼日利亚某油田的钻井资料为依据，采用本文所提出的方法对常规直井、压裂直井、常规斜井、常规水平井、压裂水平井、反向双分支水平井和均向三分支水平井进行评价和优选。基本参数见表1、表2、表3。

2.1 建立综合评价模型

2.1.1 计算初始产能值

基于等效井径理论，耦合求解压降分布模型和井筒流动模型，可求得不同井型的理论初始产能值，考虑理论计算结果的偏差，用产能修正系数（本文统一取为1.2）对理论值进行修正，计算结果见表4。

2.1.2 计算累积产油量

本文选择目前较具有代表性的Arps指数递减模型、Arps双曲递减模型、XH递减模型和YII递减模型进行计算。结合现场实际生产数据，采用灰色关联因素分析方法计算不同递减模型的关联度，结果如表5所示。

由表5可以看出，Arps双曲递减模型关联度最大，即Arps双曲递减模型预测结果与实际生产数据拟合最好。用Arps双曲递减模型预测不同井型在10年评价期内的累计产油量，计算结果如表6。

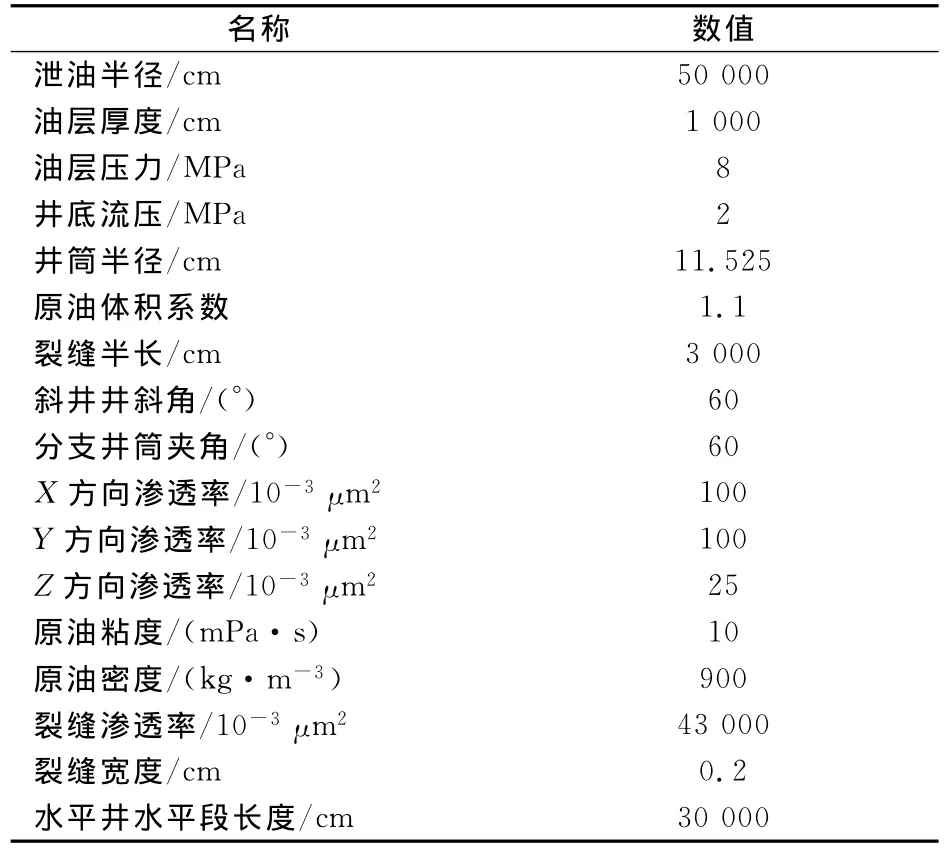
表1 地层、原油及井筒基本参数

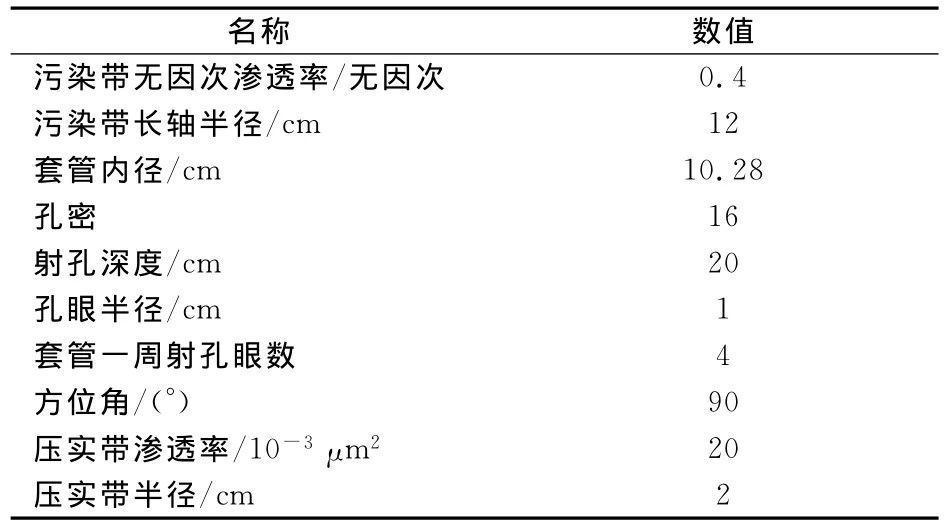
表2 射孔完井基本参数

表3 不同井型钻井经济参数

表4 理论及修正初始产能值计算结果

表5 产能递减模型关联度计算结果

表6 不同井型累计产油量计算结果

2.1.3 计算其它评价参数

结合表6所示不同井型在10年评价期内的累计产油量和表3所示不同井型钻井经济参数，运用公式（5）、（6），可求得不同井型的净现值和动态投资回收期，结果如表7。

表7 不同井型评价指标计算结果

2.2 综合评价模型分析

利用灰色关联方案决策方法，取不同井型的不同评价指标值组成比较序列，取每个评价指标的最优值组成理想井型，取理想井型各指标构成参考数列，结果如表8所示。根据表8中所求得的不同井型各评价指标计算结果，可得不同井型的灰色关联系数，见表9。基于层次分析理论，对不同评价指标赋标度值，计算不同指标的权值，如表10所示。

结合计算所得的灰色关联系数和各评价指标权值，运用公式可求得不同井型的关联度值，见表11。

由表9和表11可以看出，在该储层条件下，当只考虑初始产能值、累计产油量或净现值时，钻压裂水平井效果最优；当只考虑钻井成本时，钻常规直井效果最优；当只考虑动态投资回收期时，钻常规水平井效果最优；而当综合考虑初始产能值、累计产油量、净现值、钻井成本、动态投资回收期等多个评价指标时，钻压裂水平井可获得最优效果，其次是常规水平井，而钻常规斜井效果最差。故多目标评价方法的评价结果与单目标评价结果是不一样的，本文所提出的方法考虑更加全面、合理。