平台运动精度对ART算法图像重建质量影响的模拟

王艳飞，李公平，潘小东，方登富

（兰州大学 核科学与技术学院，兰州 730000）

工业计算机断层成像技术（Industrial Computed Tomography）是20世纪80年代发展起来的先进无损检测技术［1］。它能直观、清晰地显示试件内部图像，不受材料种类、形状结构等因素影响，被广泛用于国防、航空、航天等多个领域。

目前广泛使用的是锥束X射线系统，它在扫描速度、图像分辨力和辐射利用率等方面远远领先于平行束和扇束CT系统。传统锥束CT系统一般采用两种运动方式：一种是物体随平台运动，射线源－探测器系统保持不动；另一种是物体与平台系统保持不动，射线源－探测器系统运动。试件转动主要是指扫描平台的运动。扫描平台运动系统主要包括转台、伺服驱动器、伺服电机和多轴控制器，简称平台系统。扫描平台系统硬件制作加工时存在一定的精度误差。这种系统误差不可避免地对CT成像系统的成像质量造成一定的影响。笔者主要用计算机模拟的方法探究扫描平台系统精度误差对X射线锥束CT图像重建质量的影响趋势和规律。

1 模拟方法

1.1 锥束CT成像系统

锥束CT成像系统主要由X射线源系统、扫描工作平台系统、探测器系统和计算机系统四部分构成，如图1所示，X射线成像遵循Beer定律［2］。系统物理过程如下：X射线源发出锥束X射线，经过物体吸收衰减，穿过物体后到达探测器，被探测器探测产生电信号并转化为数字信号读出，由计算机系统接收后根据一定算法计算出物体的衰减系数分布。

1.2 ART图像重建算法

图1 锥束CT成像系统

ART算法首先将试件离散成n×n个方格，并假定每个方格中像素值是常数，fi代表第i个像素内的像素值。N＝n×n为像素总数。Pi为第i条射线的投影数。图像重建归结为解下列线性方程组：式中：M为投影总数；Wij为权因子，表示第i条射线穿过第j个像素所占权重。

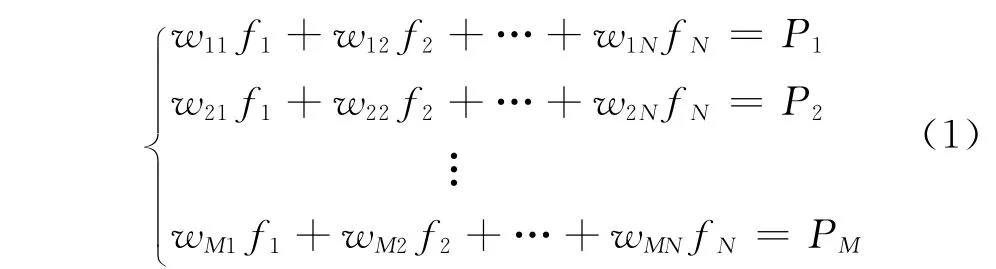
ART算法的基本思路是：先假设一初始图像向量F0，根据F0求一次近似图像F1，再根据F1求二次近似图像F2……直到满足给定精度。过程中可选择合适的松弛因子来加速算法的收敛速度［3］。

2 结果及讨论

采用VC＋＋6.0编写程序，仿真锥束CT扫描及图像重建过程。系统参数设定如下［4］：X射线源为理想点光源，能量单一；射线源最大锥角9.6°；扫描轨迹为半圆；射线源到平台及平台到探测器距离相等，均为780mm［5］；探测器阵列128×128，像元尺寸0.512mm；三维重建试件阵列128×128×128，重建体素尺寸0.256mm；扫描间隔为1°［5］；投影数为180［5］；松弛参数设定为0.25［5］。用 MATLAB7.0构造 Shepp－Logan头部模型［6－7］，该头部模型由十个椭球组成，参数见表1。其中：N0为迭代次数；x0，y0，z0为椭球的中心坐标；a，b，c分别为X，Y，Z 方向的半轴长；φ，γ，θ分别为椭球绕X，Y，Z轴逆时针旋转的角度；ρ为椭球密度，用来模拟人体断层组织对X射线的衰减系数。该模型下沿X，Y，Z轴的切面图见图2。

采用相似系数和均方差来评价数据结果：

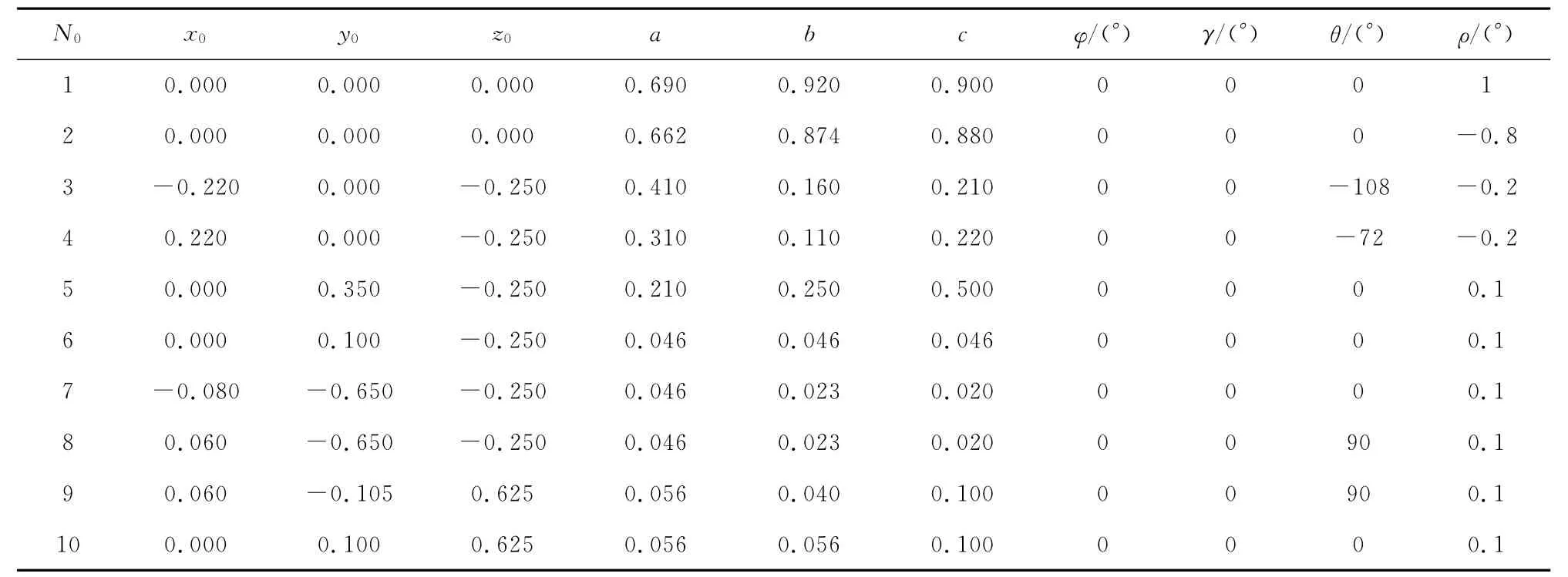
表1 头部模型参数

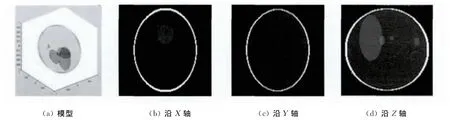
图2 Shepp－logan三维模型及其沿X，Y，Z轴的切面图

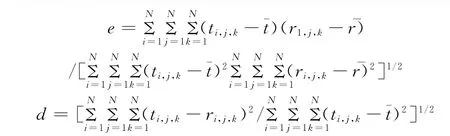
式中 ：ti，j，k，ri，j，k分别为测试模型和重建模型中第i层、j行、k列的体素密度为测试模型密度平均值，为重建模型的密度平均值；e为图像的相似系数，表示重建所得图像与原始图像模型之间的相似程度，其值越大，表示其重建图像质量越好；d为归一化均方根距离测量值，表示重建后图像真实再现测试模型图像的情况，其值越小表示其重建图像质量越好。

平台精度对图像重建的影响，主要取决于平台的运动方式：平动、转动及升降运动。程序中，平台采用PLANT＆MILL公司生产的ART330，系统精度如表2所示。采用单因素变量法和极值法观察平台精度对模拟成像质量的影响。

表2 ART330平台参数

2.1 轴向精度对图像重建的影响

由表2可知，轴向精度为2μm，即上下升降运动中，平台精度误差为±2μm，以0.5μm为间隔，观察轴向精度对图像重建的影响，结果如图3所示。其中，精度为0是指在理想状态下的模拟值，即理想值，由理想值得到的曲线称为理想曲线。由图3（a）可看出，随着迭代次数的增加，重建图像的相似系数越来越大；除理想曲线外的其它曲线间隔不明显；理想曲线与其它曲线间隔较大；其中的小图为第8次迭代的相似系数值，可看出，轴向精度不为0的曲线间差异不大，近似相等，这些曲线与理想曲线差值较大。图3（b）显示重建图像的均方差，从图中可看出，随迭代次数的增加，均方差越来越小；精度不为0的曲线均方差之间差异不大，近似相等；理想曲线的均方差与前者有明显的不同；小图中第8次迭代的均方值与相似系数的第8次迭代的结果一致。总结可知，精度不为0时各曲线间相似系数和均方值的差异不大，认为相等，可将其与理想曲线间的关系设为参数，在程序中进行修正。

2.2 水平轴精度对图像重建的影响

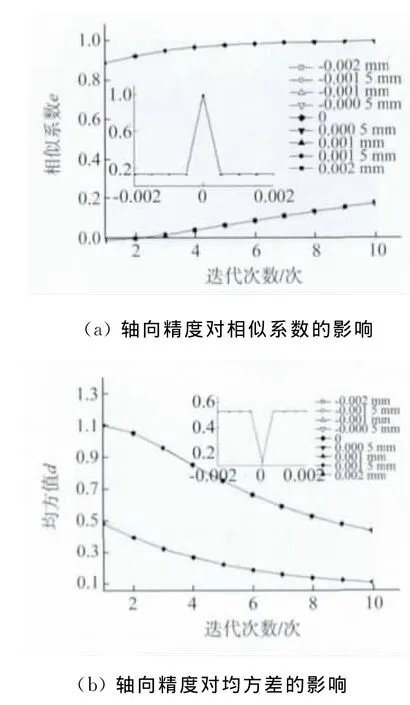
图3 轴向精度对重建图像的影响

图4 不同水平轴运动精度时的图像重建的相似系数与均方值

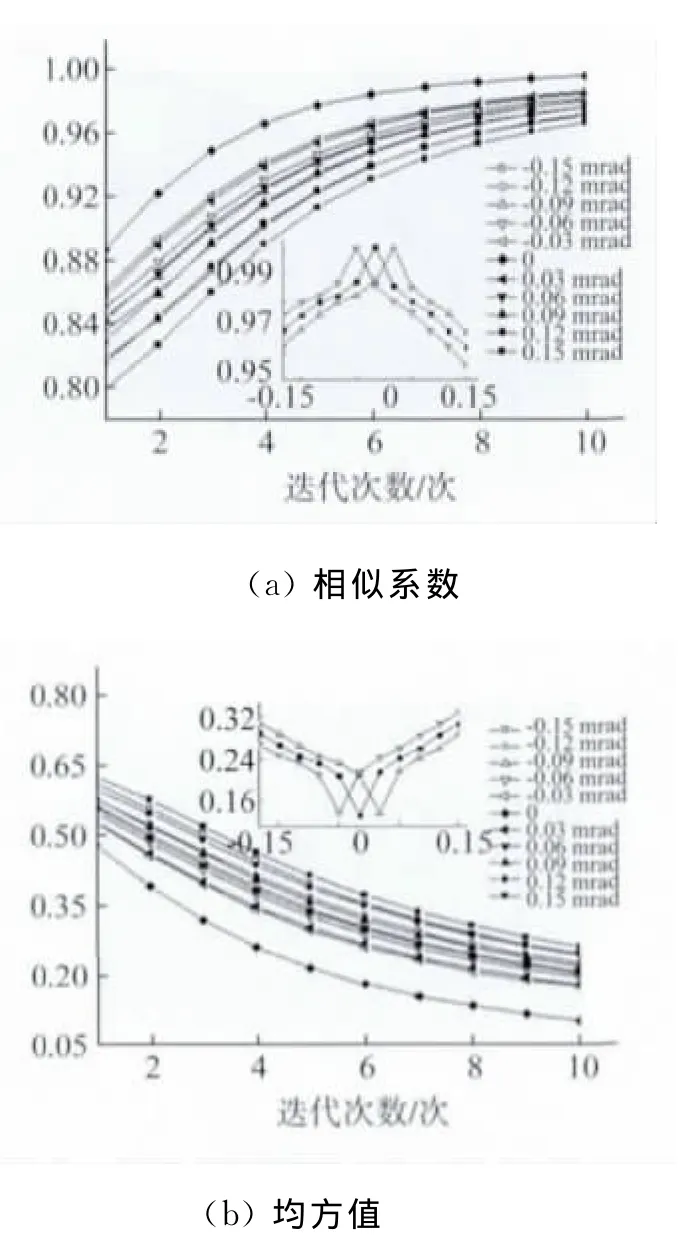
图5 不同转动精度时的图像重建的相似系数与均方值

从表2中得知，水平轴精度为8μm，即沿X轴移动时的精度为±8μm。设沿X轴正方向为正，反之为负，取间隔1μm，观察不同水平轴精度对重建图像的影响，结果如图4所示。水平轴精度为0的曲线设为理想曲线。图4（a）所示，水平轴精度不为0，与理想曲线相似系数差值很小，小图显示第8次迭代的结果。由曲线可知，水平轴精度造成的相似系数的误差在0.02%之内，差值较小，可以忽略不计。由图4（b）中可知，水平轴运动精度的均方值与精度为0时差异不大，小图显示第8次迭代的相似系数值，其最大的误差在0.2%之内。综合相似系数可知，水平轴运动精度对图像重建的影响较小，可忽略不计。

2.3 转动精度对图像重建的影响

转动过程中的精度分为两种：一种是定位精度，一种是重复精度。由表2可得知，重复转动的定位精度为0.15mrad，以0.3mrad为间隔观察不同程度的转动精度对图像重建的影响，重复率取29.1μrad，结果如图5所示。重复精度是在定位精度的基础上进行累积的。转动精度为0的曲线设为理想曲线。图5表示不同转动精度对图像重建的影响程度不同，理想曲线相似系数最大，其他精度则以0为中点向两边递减，且不对称；小图显示了第8次迭代的结果，并加入重复率的影响，这里，重复率是在定位精度的基础上进行累加的。可知，重复率影响图像的位置，使其左移（重复率为负）或右移（重复率为正），对重建图像的精度影响不大，可增加迭代次数进行修正。由图5分析可知，由于转动精度改变了射线的倾角，使其与体素的交点发生变化，影响有效长度的测量，进而影响了重建体素的密度分布，而且转动精度对重建图像的影响与物体形状、密度分布，放置方式等诸多因素有关，影响较大而又难以消除，无法在程序中进行修正。

2.4 水平面倾角对图像重建的影响

程序中假设水平面绝对水平，但这在实际试验过程中很难保证。在这里探讨水平面存在一定的倾角时对试验结果的影响。由表2知，取倾斜角为24.25μrad，从0°开始，以20°为间隔，观察不同角度的倾角对图像重建的影响。如图6（a）和（b）表示在没有倾斜的情况下，物体转动一定角度所产生的图像重建的相似系数和均方值；图7（a）和（b）表示存在倾斜角24.25μrad时，物体转动一定角度所产生的图像重建的相似系数和均方值；图8（a）和（b）表示倾斜角为24.25μrad的重建图形与无倾角时的重建图形的相似系数和均方值的差值，小图表示第8次迭代的结果。由图可知，在0°～100°时，相似系数和均方值的差值保持在0附近，误差值相对较小，可忽略不计，在100°～180°之间，相似系数和均方值差值变化剧烈，推测这与物体的形状、密度分布、放置方式有关，且无规律可循。

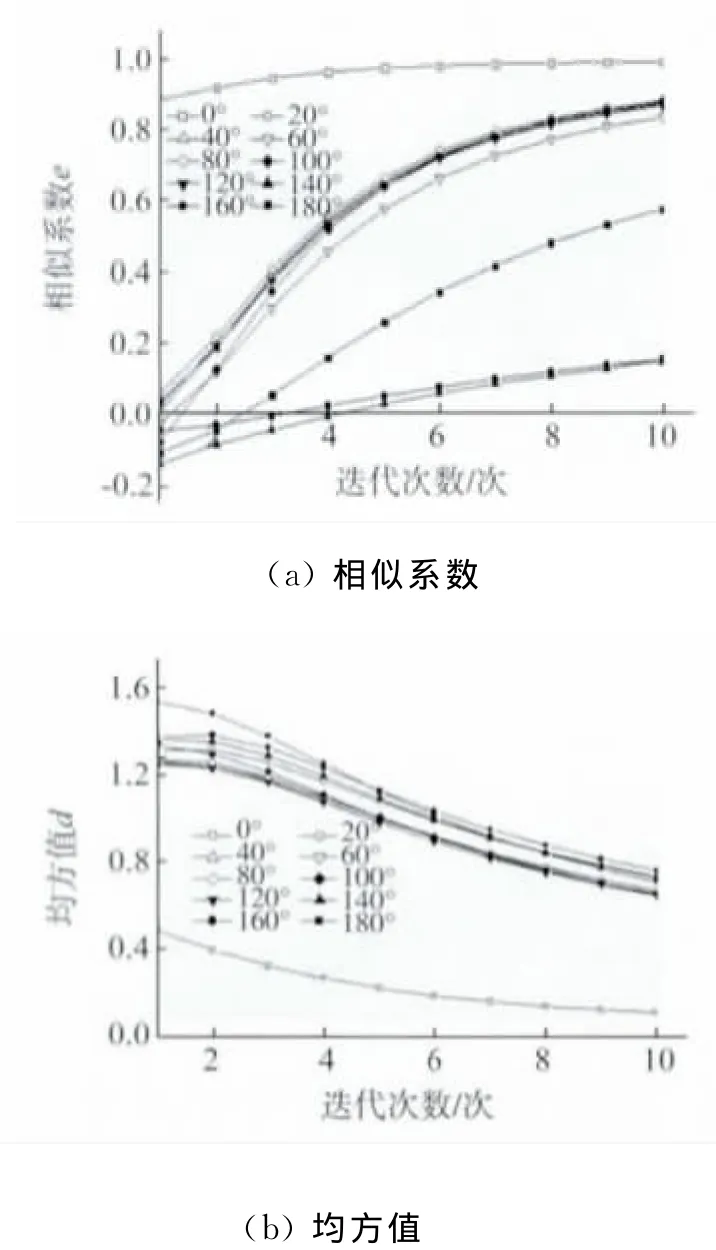
图6 无倾角时重建图像的相似系数与均方值

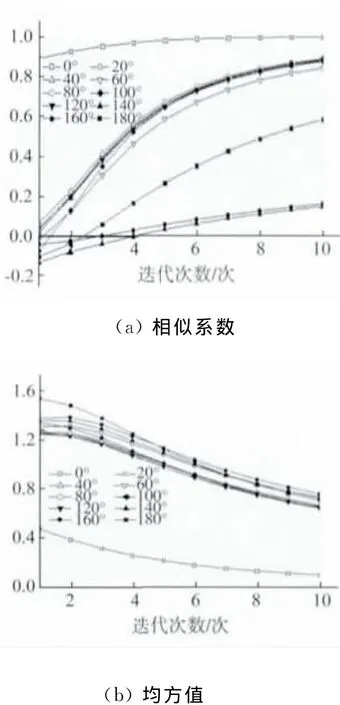
图7 倾斜角24.25μrad时 图像重建的相似系数与均方值

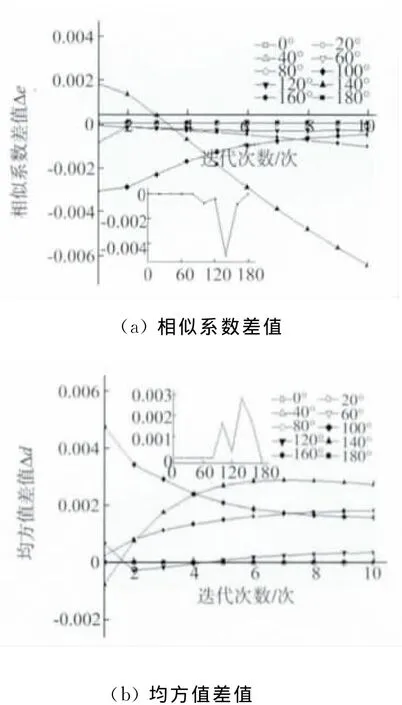
图8 倾斜角24.25μrad和无倾斜角时图像重建的相似系数与均方值的差值

3 结语

平台精度误差对图像重建具有较大影响。一般而言，轴向精度对图像的影响为一固定值，可在程序中设一系数进行修正；水平轴运动精度对图像重建的影响很小，可忽略不计；转动精度由于对图像体素单元划分造成较大影响，其所引起的误差较大且难以预测；水平面倾角对图像造成的误差与物体密度分布、放置位置等因素有关，误差较大，且难以修正。在实际CT检测中，平台运动可能是几种运动的相互叠加，情况更为复杂。在程序中对某些因素造成的误差进行校正可排除这些因素对图像重建造成的影响，使结果更趋近于真值。

［1］ 先武，李时光，王珏.最佳无损检测手段——工业CT技术的发展［J］.光电工程，1995，22（4）：52－57.

［2］ 王庆胜.航空发动机涡轮叶片缺陷检测中的关键技术研究［D］.西安：西北工业大学，2005.

［3］ 张胜利，张定华，黄魁东，等.锥束ART算法快速图像重建［J］.仪器仪表学报，2009，30（4）：887－892.

［4］ 刘远鹏，张丰收.锥束计算机断层成像系统［M］.北京：知识产权出版社，2008.

［5］ 伍建辉，李公平，周龙，等.锥束CT扫描方式对ART算法图像重建的影响研究［J］.核技术，2011，34（10）：759－764.

［6］ 刘泽，孙丰荣，李艳玲，等.基于3DShepp－Logan头部模型的三维医学图像重建仿真［J］.生物医学工程学杂志，2006，23（5）：938－943.

［7］ HENGYONG YU，SHIYING ZHAO，GE WANG.A differentiable Shepp－Logan phantom and its applications in exact cone－beam CT［J］.Phys Med Biol，2005（50）：5583－5595.