一个新混沌系统的脉冲控制与完全同步
2013-10-25张群娇
张群娇
张群娇
(武汉纺织大学 数学与计算机学院, 湖北 武汉 430073)
本文研究了文献[12]中提出的一个新混沌系统的脉冲控制与完全同步问题。基于脉冲控制的方法,得到了保证脉冲控制的混沌系统和同步误差系统在原点全局渐近稳定的一些准则。最后,数值仿真的结果证实了所提方法的有效性和可行性。
脉冲控制;完全同步;混沌系统
自从Ott 和Pecora关于混沌控制和同步的开创性工作以来[1,2], 在过去的几十年里,混沌的控制与同步问题一直是非线性科学领域的研究热点之一。人们先后提出了各种控制策略用于解决混沌的控制问题,如反馈控制,自适应控制,滑模控制,脉冲控制等等[3-11]。
事实上,由于脉冲控制的方法对于处理那些不能经受连续扰动的系统是有效的,并且,在系统同步的过程中,响应系统只需在离散的时刻接受来自驱动系统变量的信息,它显得更加地受欢迎。也因此,它已经广泛地应用于控制和同步混沌系统[8-11]。另外,从驱动系统到响应系统传输的信息量的骤减也使得这种方法在许多实际应用中更加有效用。
本文主要研究了如何利用脉冲控制的方法来稳定和同步一个新提出的混沌系统,在脉冲间隔变化的情形,得到了保证脉冲控制的混沌系统全局渐近稳定和同步的一些充分条件. 最后, 数值仿真的结果阐述了理论结果的正确性。
1 混沌系统的描述
在文献[12]中,Abooee等人提出了一个新的混沌系统,系统描述如下
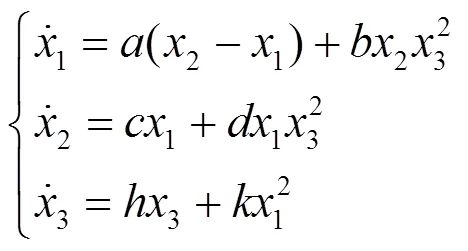
图1 新的混沌系统的吸引子
2 新混沌系统的脉冲稳定控制
把方程(1)所刻画的混沌系统的线性部分与非线性部分分开, 重写如下
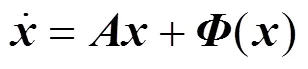
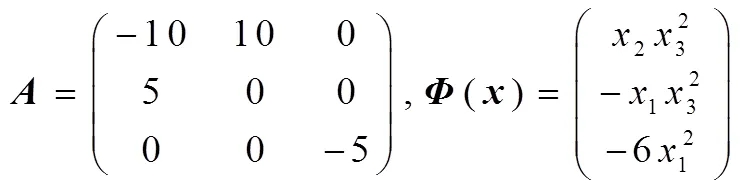
设计脉冲控制的系统方程形式如下
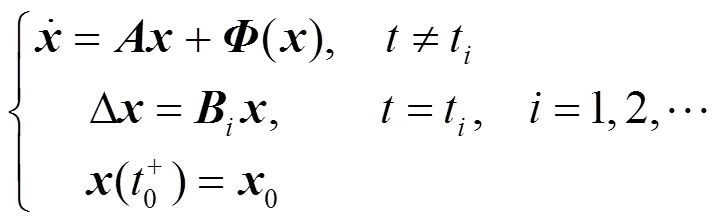
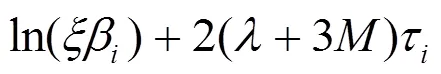
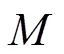
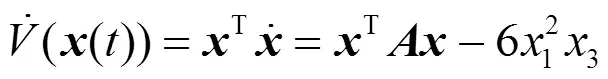
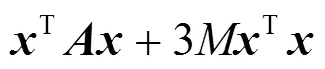
这意味着
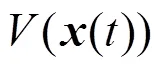
另一方面,从系统(4)的第二个方程可得
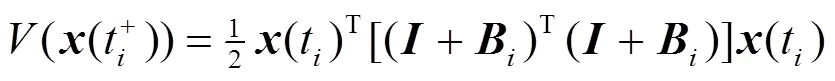
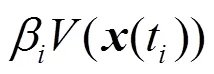
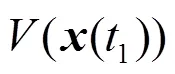
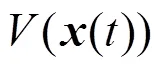
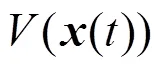
根据不等式(5)可知
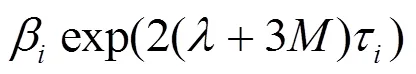
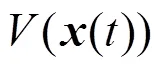
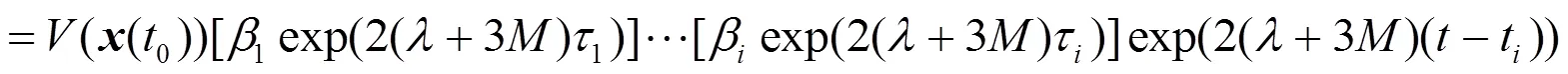
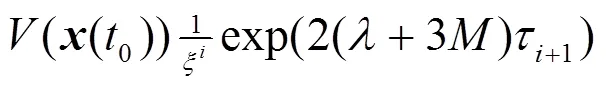
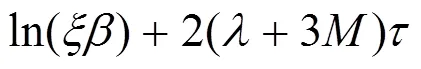
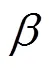
3 新混沌系统的脉冲完全同步
视方程(2)为驱动系统,设计脉冲控制的响应系统由下列脉冲方程刻画

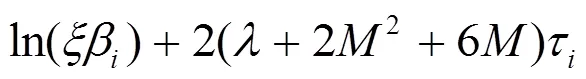
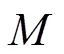
证明:由方程(2)和(12),可得脉冲同步的误差系统

这里
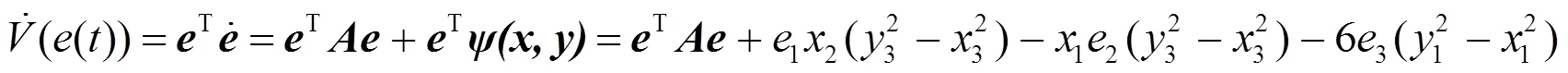
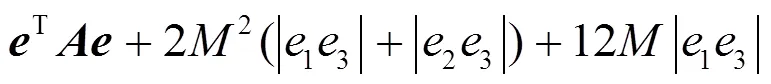
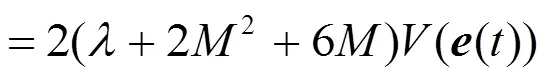
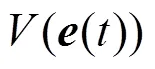
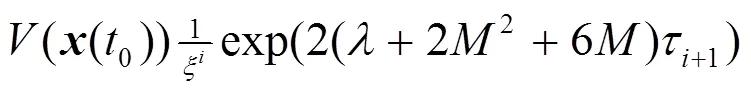
这意味着系统(14)的平凡解在原点是全局渐近稳定的。从而,脉冲控制的系统(12)与(2)就是全局渐近同步的。
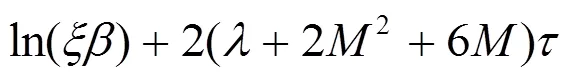
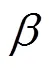
4 数值仿真
为了阐明所提方法的有效性和可行性, 这一部分给出了一些数值仿真的结果。
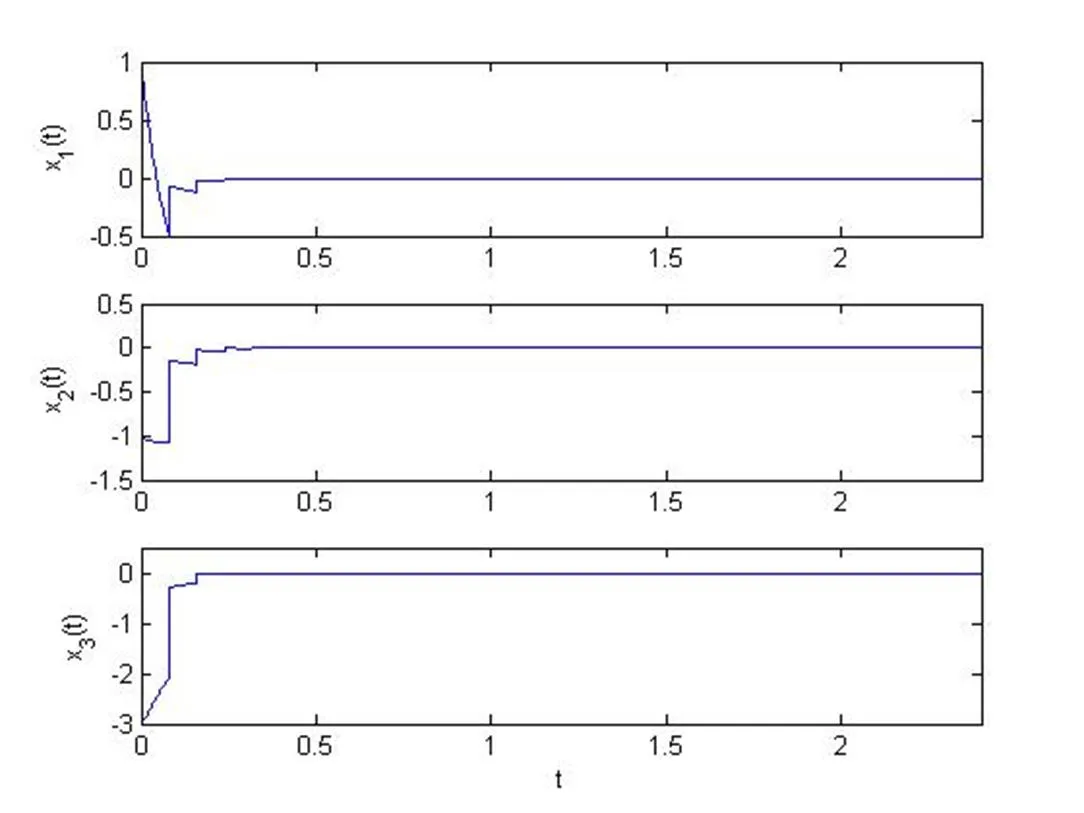
图2 ,时脉冲稳定的系统状态
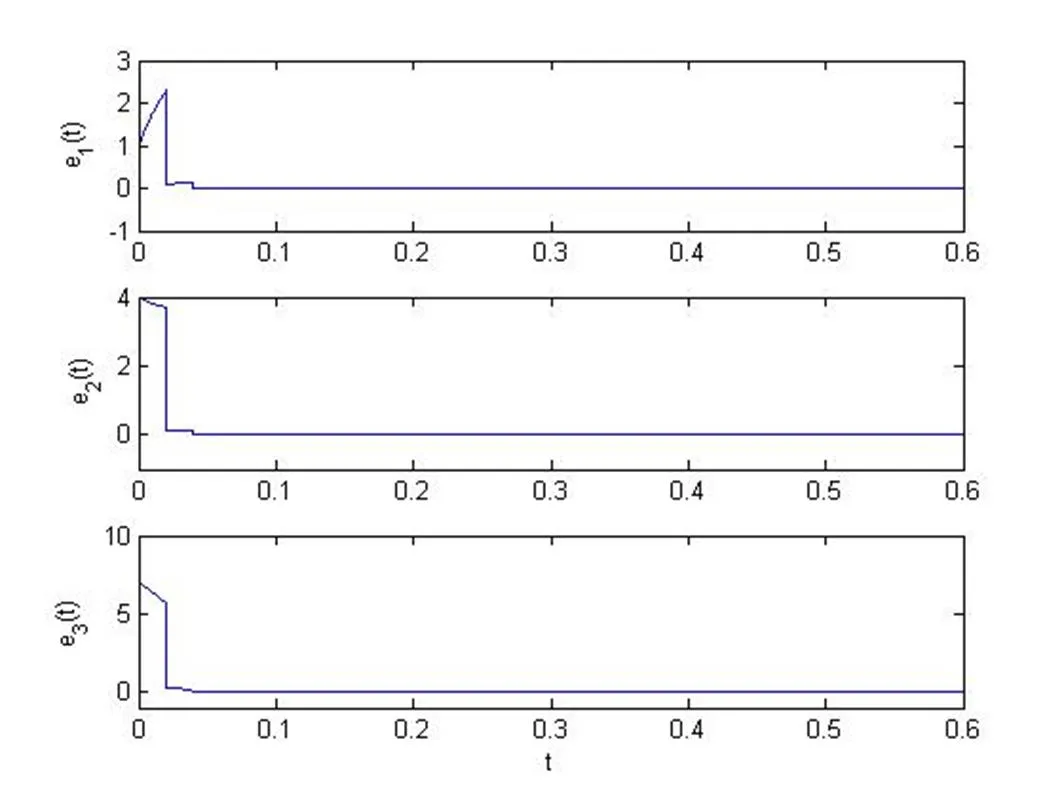
图3 ,时脉冲同步系统的误差
5 结论
本文研究了一个新的混沌系统的脉冲控制与同步问题,在脉冲间隔变化的情况得到了保证脉冲控制系统全局稳定和同步的一般性条件,并给出了特殊情形下的相应推论。最后,一些数值仿真的结果证实了所得的理论结果的正确性。
[1] Ott E, Grebogi C, Youke J A.Controlling Chaos[J].Phys Rev Lett, 1990, 64: 1196-1199.
[2] Pecora L M, Carroll T L.Synchronization in Chaotic Systems[J].Phys Rev Lett, 1990, 64: 821-824.
[3] Wang G, Yu X, Chen S.Chaos Control, Synchronization and its Application[M]. Beijing: National Defence Industry Publishing House, 2001.
[4] Wang C, Ge S.Adaptive Synchronization of uncertain chaotic System via backstepping Design[J].Chaos, Solitons and Fractals, 2001, 12:1199-1206.
[5] Chen M, Han Z. Controlling and synchronizing chaotic genesio system via nonlinear feedback control[J].Chaos, Solitons and Fractals, 2003, 17: 709-716.
[6] Chen S, Lü J.Parameters identification and synchronization of chaotic systems based on adaptive control[J].Phys Lett A, 2002, 299: 353-358.
[7] Yan J, Yang Y, Chiang T, et al.Robust synchronization of unified chaotic systems via sliding mode control[J].Chaos, Solitons and Fractals, 2007, 34:947-54 .
[8] Hu M, Yang Y, Xu Z. Impulsive control of projective synchronization in chaotic systems[J]. Phys Lett A, 2008, 372:3228–3233.
[9] Li C, Liao X, Zhang X. Impulsive synchronization of chaotic systems[J].Chaos, 2005,15:023104.
[10] Chen S, Yang Q. Impulsive Control and Synchronization of Unified Chaotic System[J].Chaos, Solitons and Fractals, 2004, 20: 751-758.
[11] Chen J, Liu H, Lu J, et al. Projective and lag synchronization of a novel hyperchaotic system via mpulsive control [J].Commun Nonlinear Sci Numer Simulat, 2011,16 :2033-2040.
[12] Abooee A, Yaghini-Bonabi H, Jahed-Motlagh M. Analysis and circuitry realization of a novel three-dimensional chaotic system [J].Commun Nonlinear Sci Numer Simulat, 2013,18:1235-1245.
Impulsive Control and Complete Synchronization of a Novel Chaotic System
ZHANG Qun-jiao
(College of Mathematics and Computer Science, Wuhan Textile University, Wuhan Hubei 430073, China)
The impulsive control and complete synchronization is investigated for a novel chaotic system [12]. Based on the impulsive method,some criteria are derived for the stability and synchronization of the impulsively controlled system. Finally, some numerical simulations are given to verify the effectiveness of the proposed theoretical results.
Impulsive Control; Complete Synchronization; Chaotic System
O 322
A
2095-414X(2013)03-0043-04
张群娇(1980-),女,副教授,研究方向:混沌控制与同步,复杂动力系统.
国家自然科学基金资助项目(11271295),湖北省教育厅科研项目(D20131602),武汉纺织大学校基金项目(2012).
