用Yangian代数解除Rb金属原子简并态

张志颖，苟立丹，白端元，周成城，肖洪亮

(1.长春理工大学理学院，长春130022;

2.长春理工大学电子信息工程学院，长春130022)

利用Yang-Baxter方程可研究量子可积问题.当其解为有理解时，它是无周期的，对应于Yangian代数［1-5］.Yangian代数是Hopf代数的一种变形，是比Lie代数更大的无穷维代数，是李代数的子代数，其物理基础为量子可积的统计模型［6-12］.Yangian代数本质是无穷维代数，由有限个生成元I和J以如下方式生成:

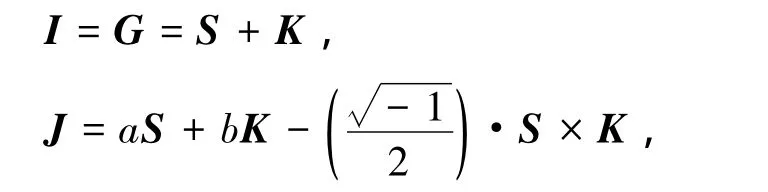
其中:I为总角动量，遵循Lie代数sl(2)对易关系;J(J+，J-，J3)为张量;a和b为任意参数.集合{I，J}形成关于sl(2)的Yangian代数，记为Ysl(2).Ysl(2)遵从如下独立对易关系:

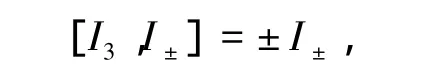
文献［13-21］给出了Yangian代数的物理意义及应用，如运用Yangian代数分析可积模型的对称性及利用Yangian算子作为升降算子实现系统本征态间的跃迁.本文利用Yangian算子，构造出新的算符，该算符可描述不同量子态间的跃迁，将其作用于系统简并的本征态上，可实现能级劈裂，从而达到解除简并态的目的.

1 Rb金属原子在Hamilton系统中的反常简并及本征态

在浓87Rb蒸汽实验中，有少量成分形成Rb2，其外层电子形成自旋衰减形式(spin-dimmer)，当外加恒磁场为特定值时，Zeeman效应产生的谱分裂消失.该Hamilton系统可表示为

式(2)当x=±1时出现简并，H存在2K+1个对应同一个本征值的本征函数，即系统为2K+1重简并［22-23］.

将Hamilton量写成一般形式:

其中:L1为轨道角动量;L2为自旋角动量.于是，可定义本征态为

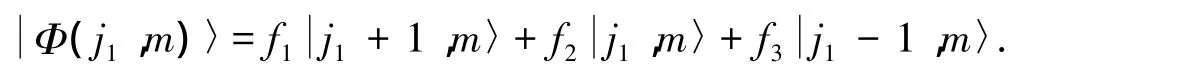
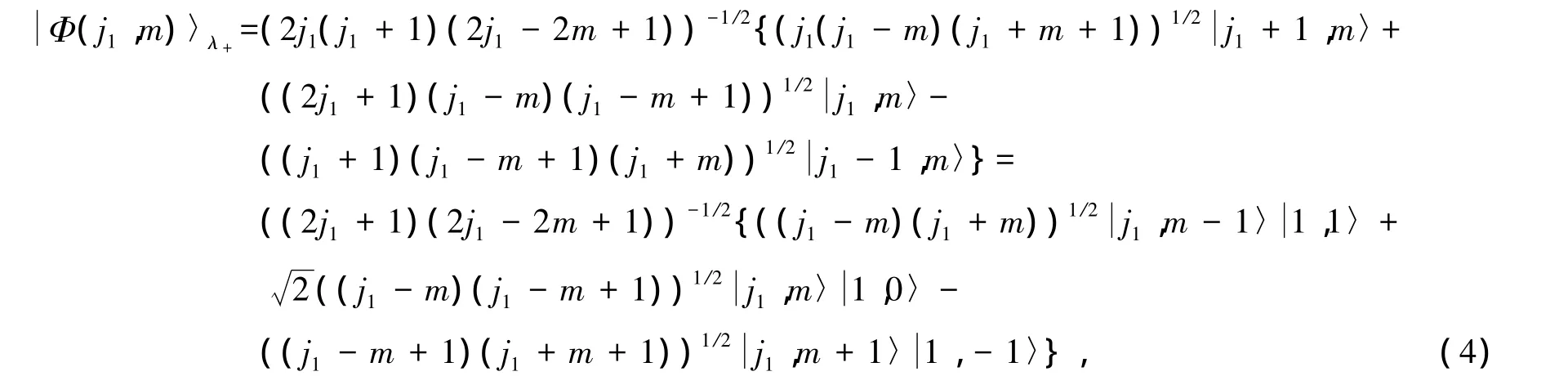
其中 m=j1+1，j1-1，…，-j1，其简并度为2j1+1.

当λ'=λ-时，波函数为

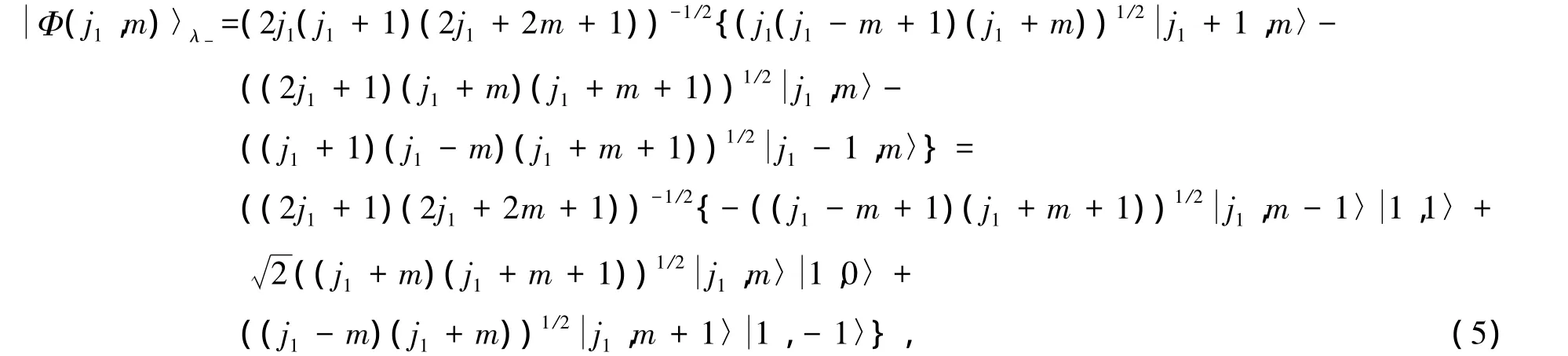
其中 m=j1，j1-1，…，-(j1+1)，其简并度为2j1+1.

2 解除系统简并态

引入由Yangian生成元组成的算符H1=J+J-和H2=J-J+.其中

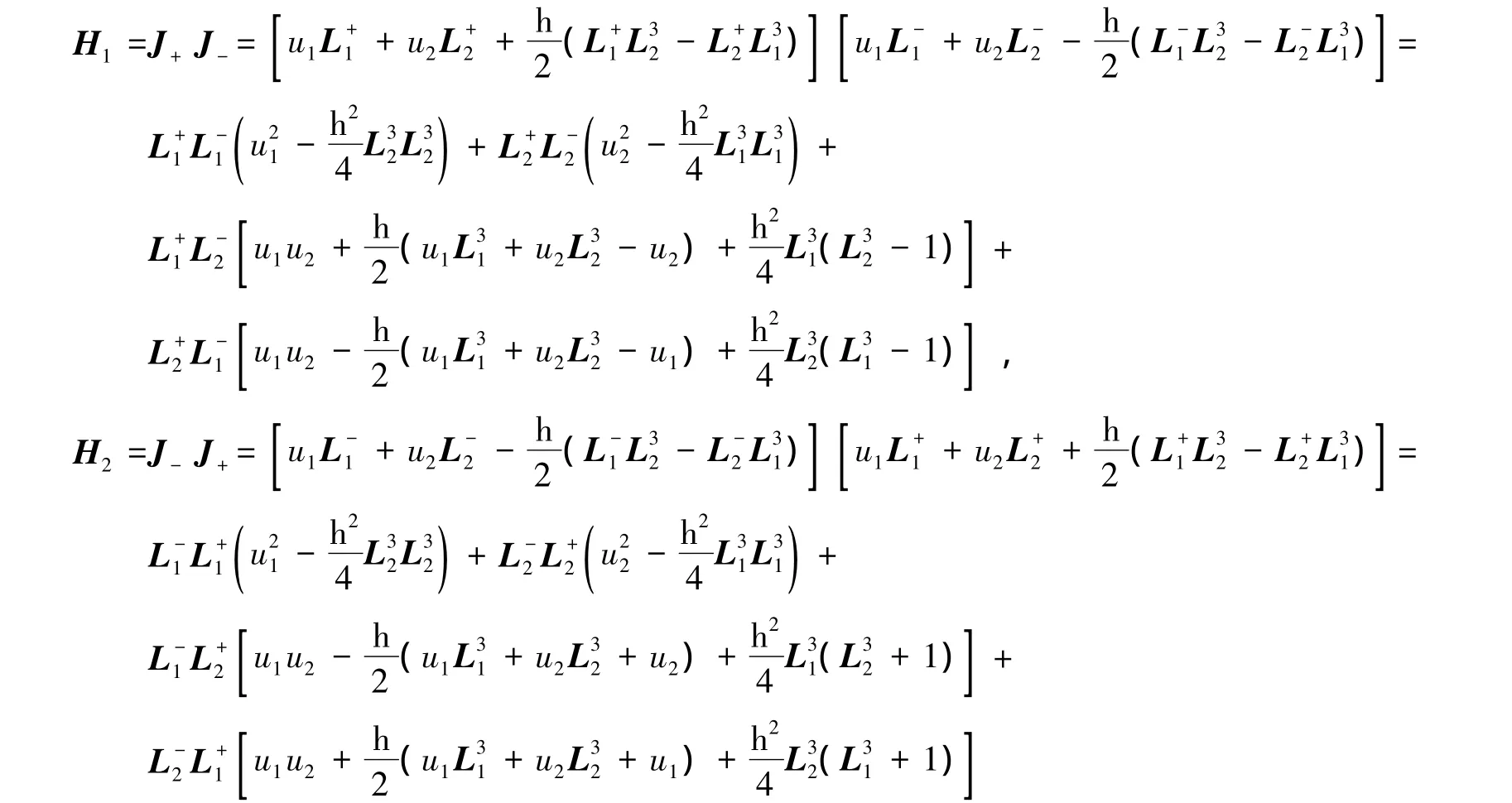
时，整个体系的Hamilton量变为H=H0+H1和H=H0+H2.

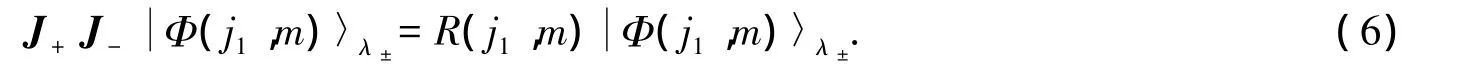
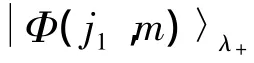
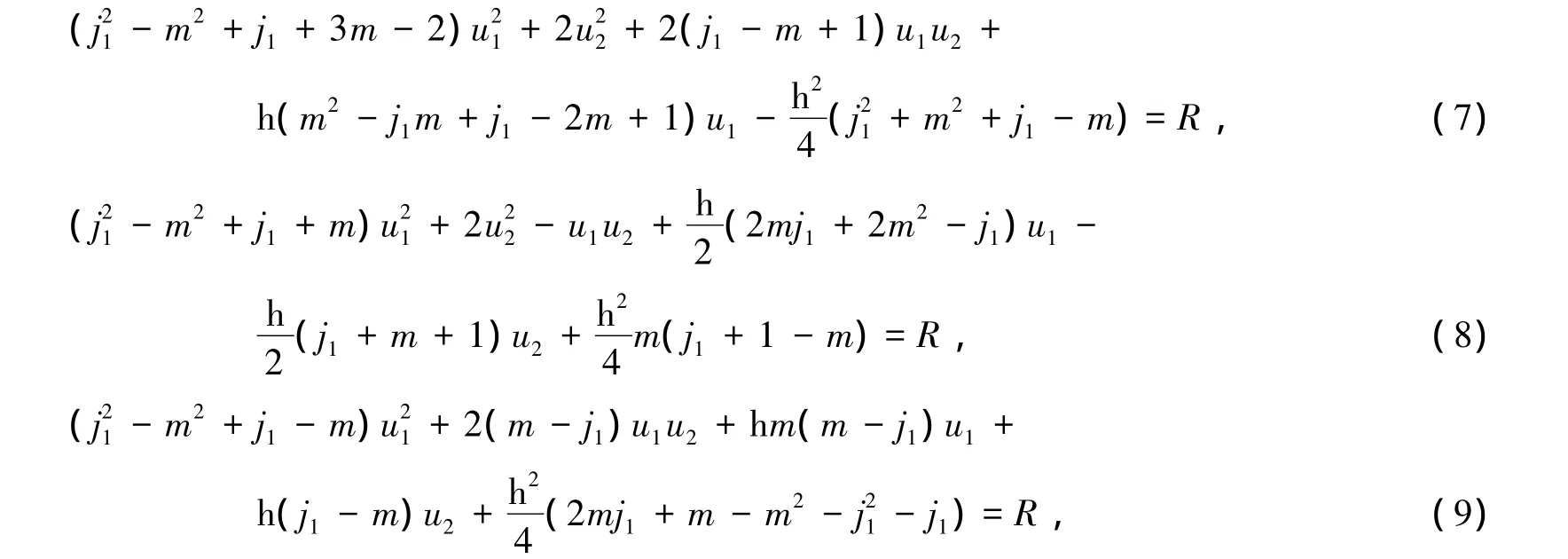
2×式(8)-式(7)-式(9)可得

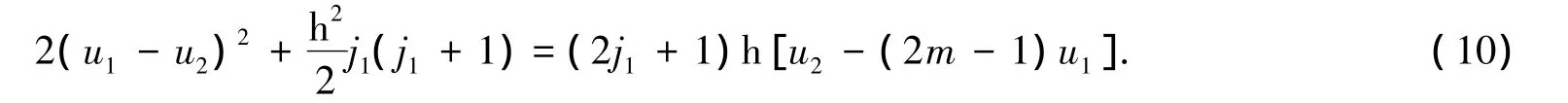
将m和j1的数值代入式(10)，并由计算机软件计算可得 u1，u2，R的解.当 j1=1，2，3时，u1，u2，R和u1-u2的值列于表1.

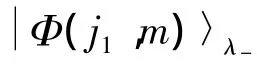
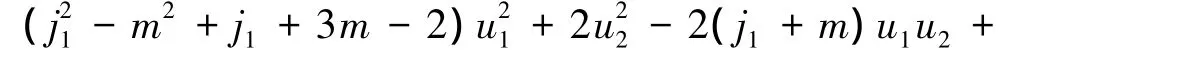
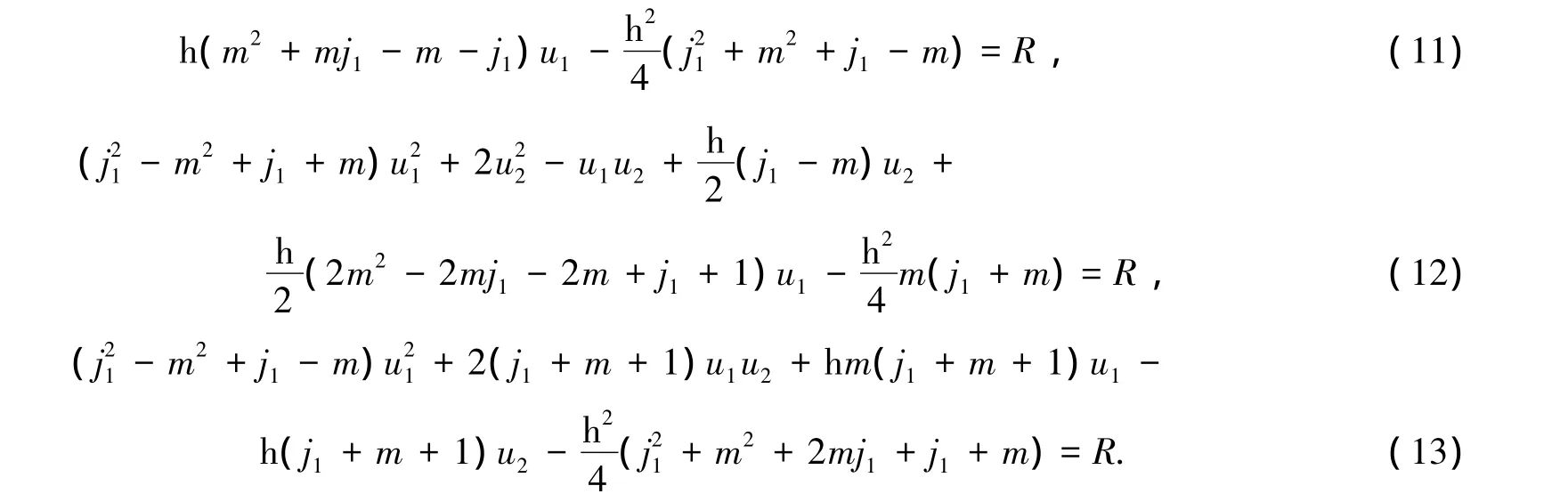
2×式(12)-式(11)-式(13)可得

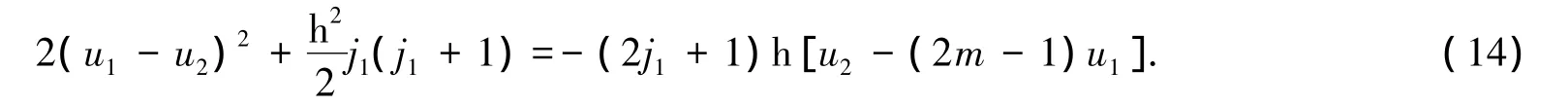
当 j1=1，2，3 时，u1，u2，R 和 u1-u2的值列于表2.

表1 对 H1=J+J-，当 λ'=λ+时，u1，u2，R 和 u1-u2的值Table 1 Values of u1，u2，R，u1-u2with H1=J+J-and λ'=λ+

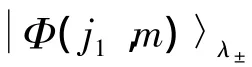
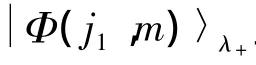
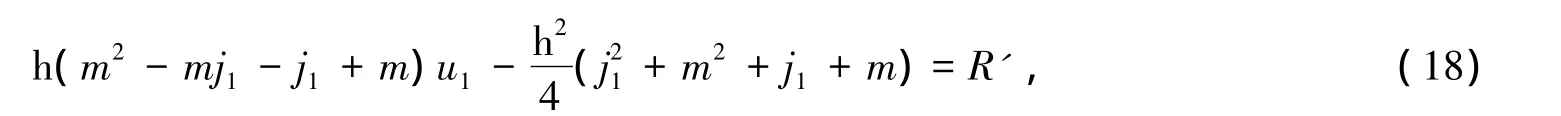
2×式(17)-式(16)-式(18)可得

当 j1=1，2，3 时，u1，u2，R'和 u1-u2的值列于表3.

表2 对 H1=J+J-，当 λ'=λ-时，u1，u2，R 和 u1-u2的值Table 2 Values of u1，u2，R，u1-u2with H1=J+J-and λ'=λ-

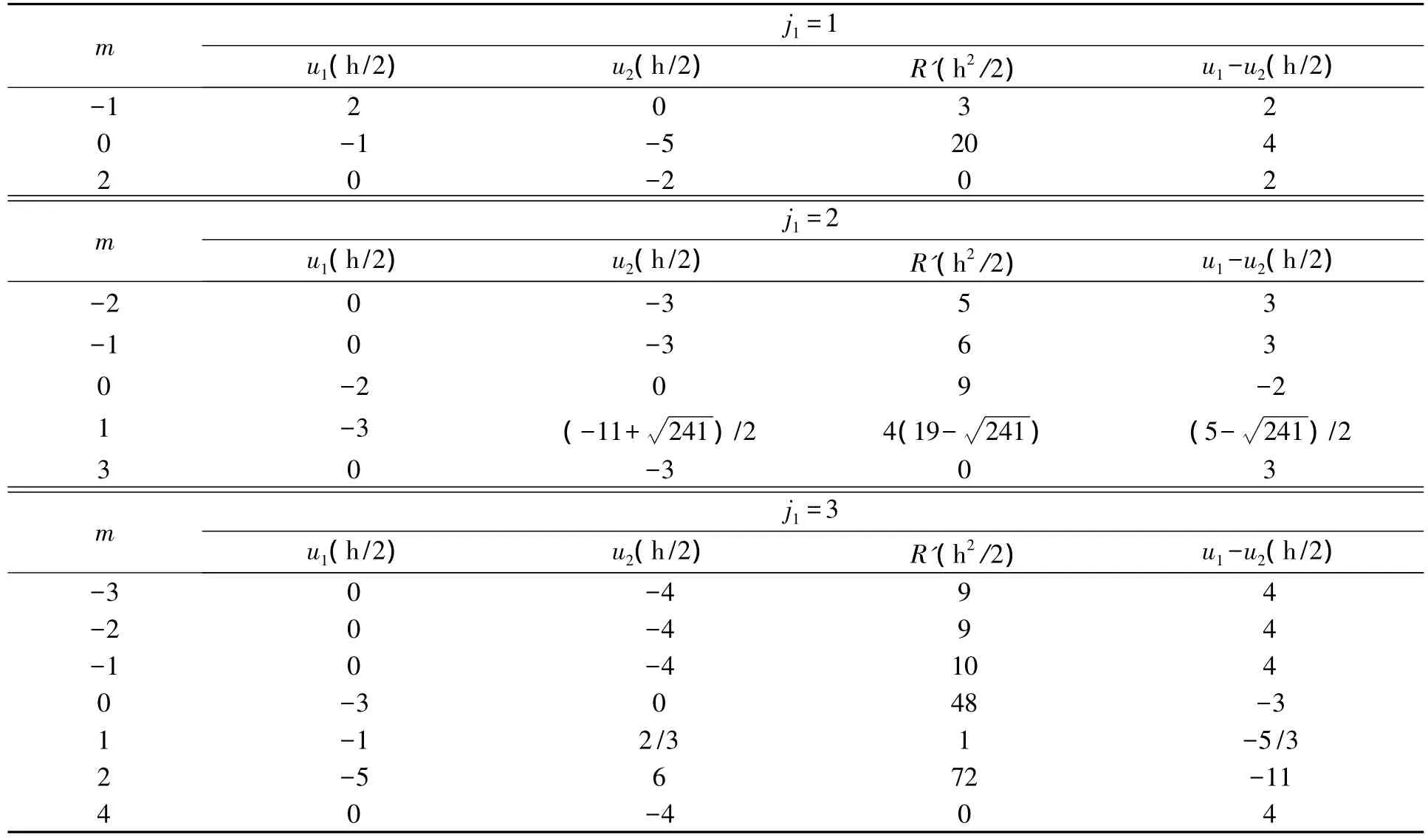
表3 对 H2=J-J+，当 λ'=λ+时，u1，u2，R'和 u1-u2的值Table 3 Values of u1，u2，R'，u1-u2with H2=J-J+and λ'=λ+

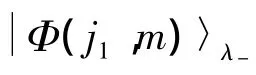
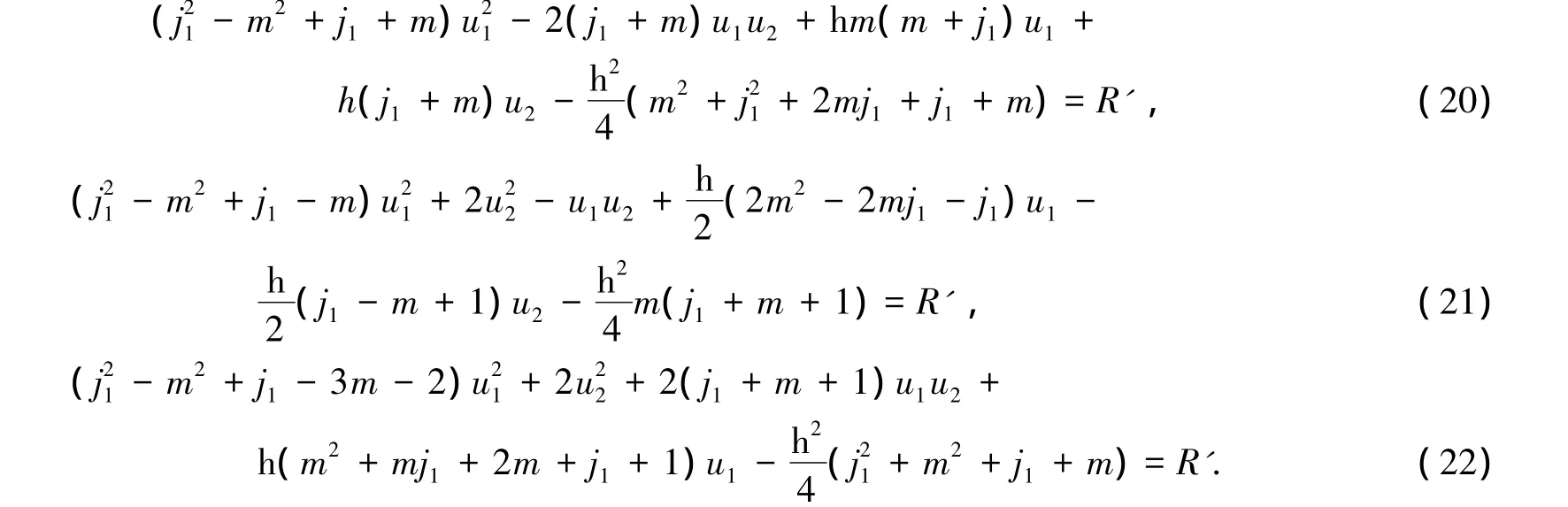
2×式(21)-式(20)-式(22)可得

当 j1=1，2，3 时，u1，u2，R'和 u1-u2的值列于表4.

表4 对 H2=J-J+，当 λ'=λ-时，u1，u2，R'和 u1-u2的值Table 4 Values of u1，u2，R'，u1-u2with H2=J-J+and λ'=λ-

综上所述，本文以Rb金属原子为模型，通过分析可知，H0=-gL1·L2+λL32的本征态为2j1+1重简并.为使简并的能级发生劈裂，引入了Yangian代数，由Yangian生成元构造了新算符H1=J+J-和H2=J-J+，使其作用于上述模型简并的本征态上，为保证H0的本征态仍为H1和H2的本征态，可得u1，u2，R和R'的限制条件，从而达到消除简并的目的.

［1］NIU Kai，XUE Kang，ZHAO Qing，et al.The Role of the l1-Norm in Quantum Information Theory and Two Types of the Yang-Baxter Equation［J］.Journal of Physics A:Mathematical and Theoretical，2011，44(26):265304.

［2］HU Tao-tao，WU Chun-feng，XUE Kang.Berry Phase and Entanglement of 3 Qubits in a New Yang-Baxter System［J］.Journal of Mathematical Physics，2009，50(8):083509.

［3］WANG Gang-cheng，XUE Kang，WU Chun-feng，et al.Entanglement and the Berry Phase in a New Yang-Baxter System［J］.Journal of Physics A:Mathematical and Theoretical，2009，42(12):125207.

［4］HU Tao-tao，WANG Gang-cheng，SUN Chun-fang，et al.Method of Constructing Braid Group Representation and Entanglement in a 9×9 Yang-Baxter System［J］.Reviews in Mathematical Physics，2009，21(9):1081-1091.

［5］SUN Chun-fang，HU Tao-tao，WANG Gang-cheng，et al.Thermal Entanglement in the Two-Qubit Systems Constructed from the Yang-Baxter R-Matrix［J］.International Journal of Quantum Information，2009，7(5):879-889.

［6］Arnaudon D，Molev A，Ragoucy E.On the R-Matrix Realization of Yangians and Their Representations［J］.Annales Henri Poincaré，2006，7(7):1269-1325.

［7］Inozemtsev V I，Inozemtseva N G，Sadovnikov B I.On the Integrals of Motion for an Exactly Solvable Model of Interacting Fermions［J］.Moscow University Physics Bulletin，2008，63(2):83-86.

［8］TIAN Li-jun，ZHANG Hong-biao，JIN Shuo，et al.Y(sl(2))Algebra Application in Extended Hydrogen Atom and Monopolemodels［J］.Commun Theor Phys，2004，41(5):641-644.

［9］SUN Chun-fang，XUE Kang，WANG Gang-cheng，et al.Entanglement and Yangian in a V3Yang-Baxter System［J］.Quantum Inf Process，2012，11(2):385-395.

［10］Stukopin V A.The Quantum Double of the Yangian of the Lie Superalgebra A(m，n)and Computation of the Universal R-Matrix［J］.Journal of Mathematical Sciences，2007，142(2):1989-2006.

［11］Stukopin V A.The Yangian Double of the Lie Superalgebra A(m，n)［J］.Functional Analysis and Its Applications，2006，40(2):155-158.

［12］CAO Xue-xia，ZHANG Liang-yun.Quantization of Dimodule Algebras and Quantum Yang-Baxter Module Algebras［J］.Journal of Mathematical Research and Exposition，2010，30(4):725-733.

［14］Stukopin V.Yangians of Classical Lie Superalgebras:Basic Constructions，Quantum Double and Universal R-Matrix［J］.Proceedings of Institute of Mathematics of NAS of Ukraine，2004，50(3):1195-1201.

［15］TIAN Li-jun，QIN Li-guo，JIANG Ying，et al.Application of Y(sl(2))Algebra for Entanglement of Two-Qubit System［J］.Commun Theor Phys，2010，53(6):1039-1042.

［16］Gerasimov A，Kharchev S，Lebedev D，et al.On a Class of Representations of the Yangian and Moduli Space of Monopoles［J］.Communications in Mathematical Physics，2005，260(3):511-525.

［17］Lucy G，Alexander M.Representations of Twisted q-Yangians［J］.Selecta Mathematica，2010，16(3):439-499.

［18］GOU Li-dan，ZHU Rui-han.A 9×9 Matrix Representation of Temperley-Lieb Algebra and Corresponding Entanglement［J］.Chin Phys B，2012，21(2):020305.

［19］WANG Gang-cheng，XUE Kang，SUN Chun-fang，et al.Quantum Phase Transition Like Phenomenon in a Two-Qubit Yang-Baxter System［J］.International Journal of Theoretical Physics，2010，49(10):2499-2505.

［20］GOU Li-dan，XUE Kang，WANG Gang-cheng.A 9×9 Matrix Representation of Birman-Wenzl-Murakami Algebra and Berry Phase in Yang-Baxter System［J］.Communications in Theoretical Physics，2011，55(2):263-267.

［21］SUN Chun-fang，WANG Gang-cheng，HU Tao-tao，et al.The Representation of Temperley-Lieb Algebra and Entanglement in a Yang-Baxter System［J］.International of Quantum Information，2009，7(6):1285-1293.

［22］BAI Cheng-ming，GE Mo-lin，XUE Kang.The Happer’s Puzzle Degeneracies and Yangian ［J］.Science in China:Series A，2002，32(4):320-329.(白承铭，葛墨林，薛康.Happer简并之谜与Yangian代数［J］.中国科学:A辑，2002，32(4):320-329.)

［23］BAI Cheng-ming，GE Mo-lin.Puzzle Degeneracies for87Rb2and Yangian Structures Appearing in Lower Excited States of Rare Gas Atoms［J］.Nuclear Physics Review，2001，18(4):232-237.(白承铭，葛墨林.87Rb2的奇怪简并与低激发惰性气体表现的Yangian结构［J］.原子核物理评论，2001，18(4):232-237.)