Sinc-Chebyshev配置方法求解一维对流扩散方程

毛 志

（ 铜仁学院 数学与计算机科学系，贵州 铜仁 554300 ）

一、引言

对流扩散方程（convection diffusion equation）是一类基本的运动方程，是描述粘性流体的非线性方程的线性化模型方程。它可以用来描述空气动力学、水力学、环境保护和生物、化学工程等众多科技和工程领域中的对流扩散问题[1]，所以关于对流扩散方程数值方法的研究具有十分重要的理论价值和现实意义。对流扩散问题的有效数值解法一直是计算数学中重要的研究内容。由于对流扩散方程同时含有对流项和扩散项，在数值求解时会引起数值振荡和数值弥散[2]，使得方程的求解比较复杂。目前，求解对流扩散方程的数值方法有多种，如有限差分法（FDM）[3]、有限元法（FEM）[4][5]、有限体积法（FVM）[6][7]、边界元法（BEM）等，其中有限差分方法是一种重要的数值计算方法。

目前对于常系数的对流扩散方程已有较多、较好的研究，而对于变系数的对流扩散方程的研究却较少，需要对方程做一定的假设。但在实际应用中，比如耦合流场的对流扩散方程，则需要研究变系数的情形[8]。基于此，本文考虑如下变系数的一维对流扩散方程的初边值问题，

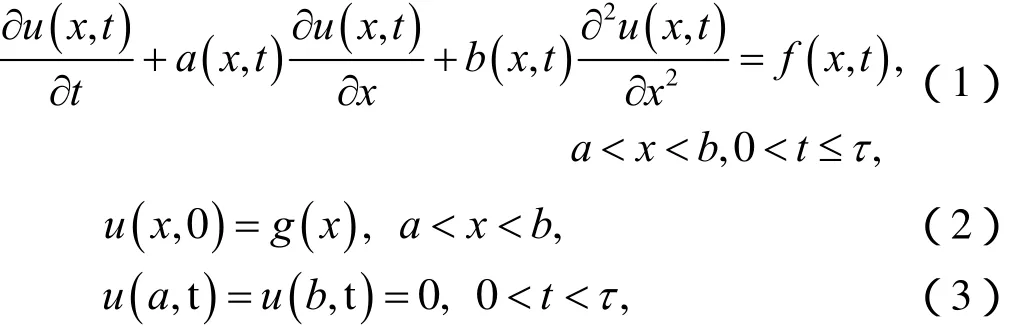
其 中a（x,t）、b（x,t）、f（x,t）和g（x）已 知 ，a（x,t ） ≠0、 b （x,t ） ≠ 0 且连续。

本文设计了一种新的求解上述问题（1）～（3）的数值方法---Sinc-Chebyshev配置方法。该方法是基于配置方法的。在空间方向和时间方向上，分别采用复合移位Sinc函数和移位Chebyshev多项式作为基函数，将方程（1）的未知解展开成一组具有未知系数的基函数和。通过选取相应的配置点后，原问题转化为线性代数方程组的求解。充分利用复合移位 Sinc函数和移位Chebyshev多项式的性质，可高效地从线性代数方程组中解出未知系数。

二、Sinc函数和移位Chebyshev多项式

（一）Sinc函数

Sinc函数具有许多优良的性质[9][10]，它被广泛地用于数值分析及积分方程、常微分方程和偏微分方程的数值求解中[11][12][13]。

在整个实轴上，Sinc函数定义如下：

下面给出具有均匀网格节点的移位 Sinc函数的表达式：

该函数在插值节点jx jh= 处有如下结论：

对于函数（）,fxxR∈，若级数

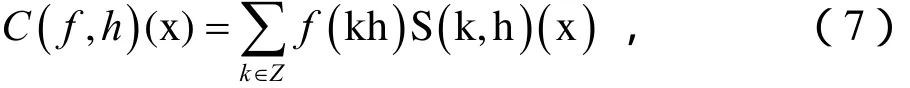
收敛，则称之为Whittaker Cardinal function。

定理1 如果 f ∈Bh，其中Bh为Paley-Wiener类函数，则；进一步，若），则

由于本文所讨论的问题是在有限区间上，故考虑如下的一一映射，

该映射将区间［a, b］--- 映射到（-∞ , +∞ ）。记映射φ的逆映射为ψ = φ-1，在它的作用下，R上均匀网格点｛kh｝k∈Z的象为：

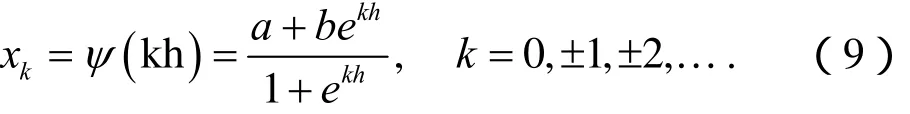
于是，需在区间［a, b］上取复合移位Sinc函数

上面的结论显示，对于 Bh上的函数，使用Sinc插值可达到指数收敛。为了构造 Sinc-Chebyshev配置方法，需要给出复合移位Sinc函数 Sφ（k, h ） （x）在节点 xk= ψ (kh), k = 0 ,± 1 ,±2 ,… 的各阶导数值，

（二）移位Chebyshev多项式

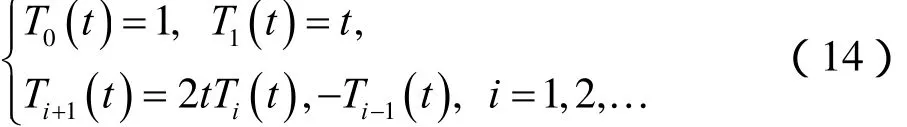
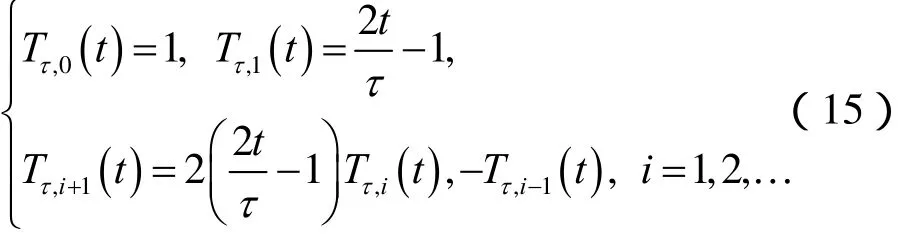
定理3 移位Chebyshev多项式 Tτ,i(t)的解析形式如下：

由于构造 Sinc-Chebyshev配置方法的需要，给出移位Chebyshev多项式 Tτ,i（ t）,i = 0 ,1,2,… 的一阶导数，

三、Sinc-Chebyshev配置方法

为了求解问题(1) ～ (3)，我们首先通过2 m +1个复合 移位 Sinc函 数Sφ（k, h ） （x） , k = 0,±1,±2,… ,±m 和n+1个 移 位Chebyshev多项式 Tτ,i（t）,i = 0 ,1,2,… ,n 逼近u（x,t）。具体如下：

引理 1 取复合移位 Sinc函数的配置点为xk,k =0,±1,±2,… ,±m（表达式(9)），有如下关系成立：

下面求解问题(1) ～ (3)。将表达式(19)代入方程(1)中可得，

在上述表达式(23)中，我们选取配置点分别为xk,k =0,±1,±2,… ,±m（表达式(9)）和tτ,n,j,j = 1,2,…,n（表达式(17)）。根据引理1可得，

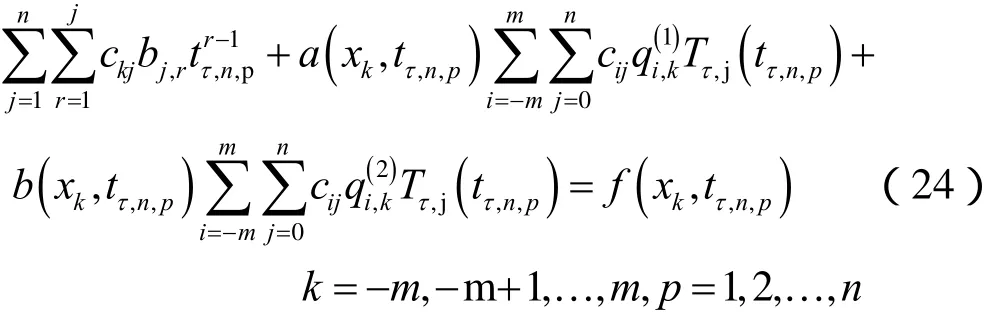
将表达式(19)代入初始条件(2)中可得，

将上述表达式(25)在2 m +1个点 xk,k =0,±1,±2,…,±m上进行配置，并利用表达式(11)可得，

于是可从表达式（24）和（26）所构成的线性方程组中解出 （2 m + 1 ） （n+ 1 ）个未知系数 cij，从而得到原问题（1）～（3）的数值解 um,n（x, t）。

四、总结

本文给出了一种求解对流扩散方程的Sinc-Chebyshev配置方法，它把求解对流扩散方程的初边值问题转化为解线性代数方程组。数值试验结果显示，该方法十分有效。下一步将尝试把该方法用于分数阶对流扩散方程[15]的求解。这与许多实际应用问题如DNA和蛋白质分子的传输[16]密切相关，具有较大的实用价值。

[1]汪继文，李付鹏，窦红．求解对流扩散方程的一种高分辨率有限体积-有限元方法[J]．水动力学研究与进展，2012，27（3）：339-347．

[2]薛禹群，谢春红．地下水数值模拟[M]．北京：科学出版社，2007，189-193．

[3]陆金甫，关治．偏微分方程数值解法（第2版）[M]．北京：清华大学出版社，2003．

[4]Katsuhiro Sakai．A new finite variable difference method with application to locally exact mumerical scheme[J]．Journal of Computational Physics， 1996,，124:：301-308．

[5]WANG Ji-wen, LIU Ci-Qun． Local discontinuous Galerkin method for radial porous flow with dispersion and adsorption[J]． Applied Mathematics and Mechanics,2004， 25（9）： 977-982．

[6]LU Biao， JIN Sheng， AI Cong-fang． A a conservative unstructured staggered grid scheme for incompressible Navier-Stokes equations[J]． Journal of Hydrodynamics，2010，22（2）： 173-184．

[7]LEEL. ． A class of high-resolution algorithms for incompressible flows[J]．Computers and Fluids， 2010，39（6）： 1022-1032．

[8]余亮．求解变系数对流扩散方程的一类新的LBGK格式[D]．武汉：华中科技大学，2008．

[9]Lund J．， Bowers K. ．Sinc methods for quadrature and differential equations[M]． Philadelphia，SIAM，1992．

[10]F． Stenger. Handbook of Sinc numerical methods[M]．New York， CRC Press，2011．

[11]Dehghan M．， Saadatmandi A.． The numerical solution of a nonlinear system of second-order boundary value problems using the Sinc-collocation method[J]．Math Comput Model，2007，46：1434-1441．

[12]Parand K.，Dehghan M.，Pirkhedri A. ． Sinc-collocation method for solving the Blasius equation[J]．Phys Lett A，2009，373： 4060–4064．

[13]Rashidinia J．， Zarebnia M. ．The numerical solution of integro-differential equation by means of the Sinc method[J]．Applied Math Comput，2007， 188： 1124–1130．

[14]李庆扬，王能超，易大义．数值分析（第5版）[M]．北京：清华大学出版社，2008．

[15]常福宣，陈进，黄薇．反常扩散与分数阶对流-扩散方程[J]．物理学报，2005，54（3）：1113．

[16]Haw Yang， Guobin Luo， Pallop K．，Tai-Man Louie， Ivan Rech，Sergio Cova, Luying Xun，X．Sunney Xie．Protein conformational dynamics probed by single-molecule electron transfer[J]．Science，2003，5643：262–266．