广义信息集博弈Nash平衡的本质连通区

孙修勇

（ 凯里学院 数学科学学院，贵州 凯里 556011 ）

1．引言

近年来，博弈论的研究及应用非常活跃，一直是学界关注的焦点。从1994年诺贝尔经济学奖授予三位博弈论专家至今，一共有六届诺贝尔经济学奖与博弈论的研究有关。一方面,博弈论在不断地拓展其应用领域,另一方，面博弈论的研究者们正致力于解决博弈理论本身不断出现的严峻问题。

Nash平衡是非合作博弈理论的核心概念。每一局中人如何通过个人的理性预测到共同的平衡点，是实际问题中Nash平衡能否真正产生的关键。近年来，Nash平衡的多重性成为博弈论本身，及其应用研究中最为棘手的问题。作为以解释实际现象和解决现实问题为己任的重要理论，博弈论面临的最大困惑是：平衡点不止一个，甚至有无穷多个。在实际问题中，不同的局中人如何通过个人的理性一致地预期到同一个平衡点？也就是说，平衡能否真正意义上实现？

多个Nash平衡带来的这一重大缺陷，一直是博弈论研究者关注的焦点。从20世纪60年代开始，寻求改进和精炼Nash平衡的机制和方法一直是博弈论研究最活跃的领域。这其中包括了1994 年Selten和 Harsanyi获得诺贝尔奖的成果---“子博弈精炼Nash平衡”、“颤抖的手的均衡”和“贝叶斯Nash平衡”等，也包括2007年度诺贝尔经济学奖获得者Myerson提出的“恰当平衡”，Kreps和Wilson提出的“序贯平衡”等精炼Nash平衡的概念。[1]2005年度诺贝尔经济学奖获得者Aumann和Schelling也曾分别提出过“强均衡”和“聚点均衡”的概念。

围绕平衡的精炼，1986年Kohlberg与Mertens[2]建立的KM平衡概念（即策略稳定集（Strategic Stable Set））是Nash平衡精炼的标志性成果。KM平衡可以归结为稳定性的方法，即策略集扰动（颤抖）意义下Nash平衡点集的极小本质集。KM平衡之所以成为Nash平衡选择和精炼的一个重要里程碑，是因为它总结了众多精炼Nash平衡的概念，并由此提出公理化的框架。令人遗憾的是，Kohlberg和Mertens提出的稳定集无法完全满足他们所给出的KM条件。之后，Mertens、Hillas等人曾经围绕稳定集的概念作过一些修正和改进[3-6]，甚至加上了拓扑同伦等一些实际意义不十分明朗的数学化条件。因为平衡的多重性是博弈论不得不正视的缺陷，围绕平衡的选择和精炼，新的结果在不断地涌现[7-15]，但多重 Nash平衡所带来的问题始终未能得到很好的解决。

针对Nash平衡的多重性，寻求一种普遍认可的机制，尤其是实际意义较为明朗的精炼机制（不完全是纯数学意义的），是决定博弈理论能否更加合理地解释实际问题的关键。本文将通过对广义信息集的方法研究Nash平衡的本质连通区问题。

2．预备知识

局中人的策略集：对于每一iN∈，非空集合iX为局中人i的策略集，记

也可将此广义博弈简记为ΓG= N;X;G;f 。

则称*x为广义博弈GΓ的Nash平衡点。

3．广义博弈Nash平衡的本质连通区

（ⅰ）对于每一iN∈，iX为线性拓扑空间中紧凸子集；

（ⅱ）对于每一iN∈，if在X上连续；

则广义博弈GΓ存在Nash平衡点。

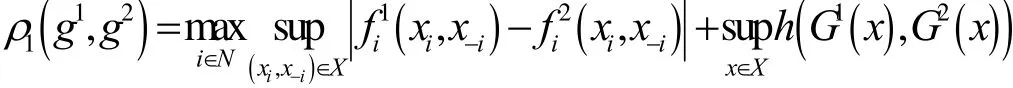
其中h为 K （X）上的Hausdorff度量，则ρ1为M1上的度量。

证明：由Φ关于一致度量的完备性及1ψ关于一致Hausdorff度量的完备性即可给出证明。

设广义博弈

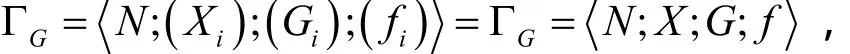
由上述定义，不难验证下面的引理。

引理 2*xX∈为广义信息博弈的Nash平衡点当且仅当 x*为最优反应映射的不动点。

定理2 设广义博弈

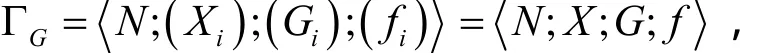
关于M的强本质连通区，设为 c（f, IG,θ）。于是，对任意的0ε﹥，存在0δ﹥，使得对于所有满足）的，有

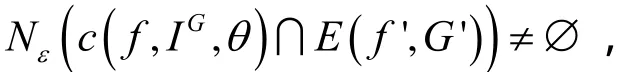
[1]D．Fudenberg，J．Tirole， Game Theory， MIT Press， 1998．

[2]E． Kohlberg and J. F. Mertens, On the strategic stability of equilibria，Econometrica，54 （1986），1003-1037．

[3]J．F．Mertens，Stable equilibria-A reformulation，Part I：Definition and Basic Properties, Mathematics of Operations Research，14（1989）， 575-625．

[4]J．F．Mertens，Stable Equilibria - A Reformulation，Part II：Discussion of the Definition and Further Results.Mathematics of Operations Research，16（1991），694-753．

[5]J．F，Mertens，Ordinality in non cooperative games，International Journal of Game Theory，32（2003），387-430．

[6]J．Hillas，On the definition of the strategic stability of equilibria，Econometrica，58（1990）， 1365-1390．

[7]J．Hillas，M．Jansen，J．Potters and D．Vermeulen，On the Relation Among Some Definitions of Strategic Stability，Mathematics of Operations Research，26：3（2002）．

[8]E．Van Damme，Strategic Equilibrium，in R. Aumann and S．Hart （eds．） HANDBOOK OF GAME THEORY，Vol．3，Chapter 41，Amsterdam：Elsevier，2002．

[9]S．Govindan and J．F．Mertens，An equivalent definition of stable equilibria，Intenational Journal of Game Theory，32（2003），339-357．

[10]S．Govindan and R．Wilson，Maximal Stable Sets of Two-Player Games，International Journal of Game Theory，30：4（2001），557-566．

[11]S．Govindan and R．Wilson， Axiomatic Justification of Stable Equilibria， Econometrica．

[12]S．Govindan and R．Wilson, Characterization of Hyperstability， Econometrica．

[13]J．Yu．Essential quilibria for n-person Noncooperative Games，Journal of Mathematical Economics，1999，31：361-372．

[14]Yu，S．W．Xiang，On essential component of the set of Nash equilibrium points，Nonlinear Analysis，1999，38：259-264．

[15]S．W．Xiang，Gui-dong Liu and Yong-hui Zhou．On the strongly essential components of Nash equilibria of infinite n-person games with quasiconcave payoffs，Nonlinear Analysis，2005，63：e2639- e2647．