三重复合修正的Ishikawa迭代序列强收敛性*

2013-10-25罗红平王元恒

浙江师范大学学报（自然科学版） 2013年1期

关键词：有界不动点收敛性

罗红平, 王元恒

(浙江师范大学数理与信息工程学院,浙江金华 321004)

三重复合修正的Ishikawa迭代序列强收敛性*

罗红平, 王元恒

(浙江师范大学数理与信息工程学院,浙江金华 321004)

在具有一致Gateaux可微范数的实Banach空间中引进了一个新的关于非扩张映像三重复合修正的 Ishikawa迭代序列,并证明了该序列在一定条件下的强收敛性.所得结果改进和推广了相应结果.

一致Gateaux可微范数;非扩张映像;三重复合修正的Ishikawa迭代;强收敛性

0 引言

非扩张映像不动点理论和算法是非线性泛函分析理论及应用中的一个重要课题,历来受到学者们的广泛关注,并得到了许多结果[1-6].2005年,Kim等[1]提出了如下修正的Mann迭代逼近非扩张映像不动点问题:

2007年,姚永红等[7]又提出了如下一个新的Mann-Halpern混合迭代算法:

并证明了在具有一致可微的实Banach空间中,序列{xn}在一定条件下强收敛到非扩张映像的某一不动点.2009年,宣渭峰等[8]提出了一个双复合修正的Ishikawa迭代算法

并证明了在一定条件下,序列{xn}强收敛到T的不动点.2011年,傅湧[9]在Hilbert空间中给出了非扩张映射Noor混合迭代序列,并且给出了该迭代序列强收敛于不动点的充分必要条件和弱收敛于不动点的充分条件.

本文则在文献[7-9]的基础上,在一致Gateaux范数可微的实Banach空间中,引入如下三重复合修正的Ishikawa迭代算法:

式(4)中,{αn},{βn},{γn},{α′n},{β′n},{γ′n},{α"n},{β"n},{γ"n}是[0,1]中的数列.并证明了当这些序列满足适当条件时的强收敛性,其结果推广了文献[7-9]的相关结果.

1 预备知识

设X是一实Banach空间,C是X中的一闭凸子集.若对任给的x,y∈C,有‖Tx-Ty‖≤‖x-y‖,则称映像T:C→C为非扩张的.用F(T)表示T的不动点集.

设X*是Banach空间X的对偶空间，J:X→2X*是由下式定义的正规对偶映像：

J(x)={f∈X*:〈x,f〉=‖x‖2,‖x‖=‖f‖},x∈X.

ρx(t)=sup{(‖x+y‖+‖x-y‖)/2 - 1:‖x‖=1,‖y‖=t}.

引理1[10]设E是实Banach空间,J:E→2E*是正规对偶映像，则对∀xy∈E及对∀j(x+y)∈J(x+y),有

‖x+y‖2≤‖x‖2+2〈y,j(x+y)〉.

引理2[11]设{xn},{yn}是Banach空间中的有界序列,xn+1=(1-βn)yn+βnxn,∀n≥0, 其中系数{βn}是[0,1]中的序列.若{xn},{yn}及{βn}满足:

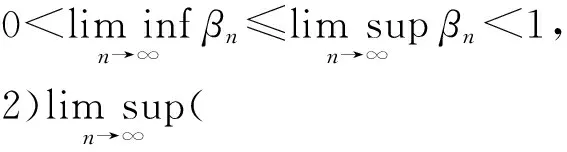
引理3[12]设{αn}是一非负实数列，使得αn+1≤(1-γn)αn+δn,n≥0,其中{γn}是(0,1)中的一数列,{δn}是R中的一数列,满足

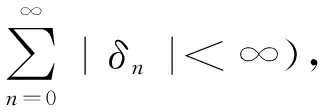
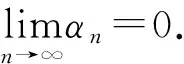
2 主要结果

定理1设C是具有一致Gateaux可微范数的实Banach空间X中的非空闭凸子集,T:C→C是具有非空不动点集F(T)的非扩张映像.设u,x0均为C中任给的点,当t→0时,vt强收敛到T中的不动点,其中vt是满足vt=tu+(1-t)Tvt的唯一确定元.并设{αn},{βn},{γn},{α′n},{β′n},{γ′n},{α"n},{β"n},{γ"n}是[0,1]中的实数列,且满足以下条件：

证明第1步证明{xn}有界.取p∈F(T),则

‖zn-p‖=‖α"nu+β"nxn+γ"nTxn-p‖≤α"n‖u-p‖+β"n‖xn-p‖+γ"n‖Txn-p‖≤

α"n‖u-p‖+(β"n+γ"n)‖xn-p‖;

(5)

‖yn-p‖=‖α′nu+β′nxn+γ′nTzn-p‖≤

α′n‖u-p‖+β′n‖xn-p‖+γ′n‖Tzn-p‖≤

α′n‖u-p‖+β′n‖xn-p‖+γ′n‖zn-p‖≤

α′n‖u-p‖+β′n‖xn-p‖+γ′nα"n‖u-p‖+(γ′nβ"n+γ′nγ"n)‖xn-p‖=

(α′n+γ′nα"n)‖u-p‖+(β′n+γ′nβ"n+γ′nγ"n)‖xn-p‖;

(6)

‖xn+1-p‖=‖αnu+βnxn+γnyn-p‖≤

αn‖u-p‖+βn‖xn-p‖+γn‖yn-p‖≤

αn‖u-p‖+βn‖xn-p‖+(γnα′n+γnγ′nα"n)‖u-p‖+(γnβ′n+γnγ′nβ"n+γnγ′nγ"n)‖xn-p‖=

(αn+γnα′n+γnγ′nα"n)‖u-p‖+(βn+γnβ′n+γnγ′nβ"n+γnγ′nγ"n)‖xn-p‖≤

(αn+γnα′n+γnγ′nα"n+βn+γnβ′n+γnγ′nβ"n+γnγ′nγ"n)max{‖u-p‖,‖xn-p‖}=

max{‖u-p‖,‖xn-p‖}.

(7)

由式(7)及归纳法可得‖xn-p‖≤max{‖x0-p‖,‖u-p‖},故{xn}是有界的，同时{yn},{zn},{Txn}也是有界的.

‖zn+1-zn‖=‖α"n+1u+β"n+1xn+1+γ"nTxn+1-α"nu-β"nxn-γ"nTxn‖≤

an+‖xn+1-xn‖.

|γ"n+1-γ"n|=|(1-β"n+1-α"n+1)-(1-β"n-α"n)|≤|β"n+1-β"n|+|α"n+1-α"n|,

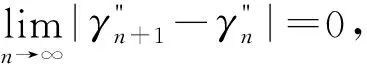
设λn=βn+γnα′n,定义序列{ln}满足xn+1=λnxn+(1-λn)ln，有

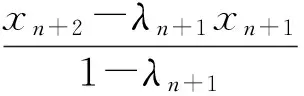
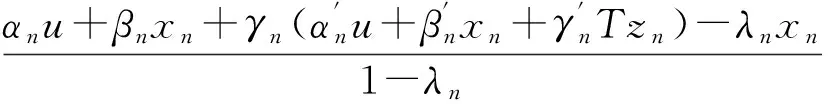
因此,

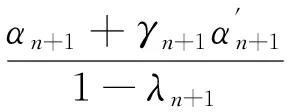
‖xn-Txn‖≤‖xn+1-xn‖+‖xn+1-Txn‖≤

‖xn+1-xn‖+αn‖u-Txn‖+βn‖xn-Txn‖+γn‖yn-Txn‖≤

‖xn+1-xn‖+αn‖u-Txn‖+βn‖xn-Txn‖+γnα′n‖u-Txn‖+

γnβ′n‖xn-Txn‖+γnγ′n‖Tzn-Txn‖≤

‖xn+1-xn‖+(αn+γnα′n)‖u-Txn‖+(βn+γnβ′n)‖xn-Txn‖+γn‖zn-xn‖≤

‖xn+1-xn‖+(αn+γnα′n)‖u-Txn‖+(βn+γnβ′n+γnγ′nγ"n)‖xn-Txn‖+γnγ′nα"n‖u-xn‖,所以

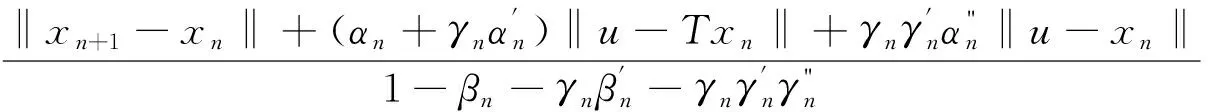
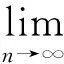
‖xn-Txn‖=0.

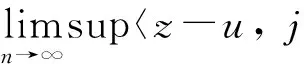
vn-xn=tn(u-xn)+(1-tn)(Tvn-xn).

由引理1得

‖vn-xn‖2≤(1-tn)2‖Tvn-xn‖2+2tn〈u-xn,j(vn-xn)〉≤

(1-tn)2(‖Tvn-Txn‖+‖Txn-xn‖)2+2tn〈u-vn,j(vn-xn)〉+2tn‖vn-xn‖2≤

(1-tn)2‖vn-xn‖2+(1-tn)2‖Txn-xn‖(2‖Tvn-Txn‖+‖Txn-xn‖)+2tn‖vn-xn‖2=

(1-tn)2‖vn-xn‖2+2tn‖vn-xn‖2+bn.

故

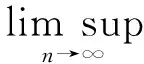
因为

〈vn-u,j(vn-xn)〉=〈z-u,j(z-xn)〉+〈z-u,j(vn-xn)-j(z-xn)〉+〈vn-z,j(vn-xn)〉,

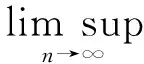
由于J在X上的任一有界子集上是范数-弱*一致连续的,所以,

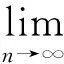
从而

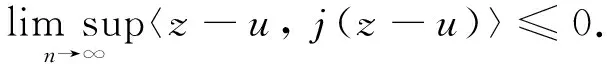
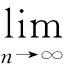
‖yn-z‖2≤α′n‖u-z‖+β′n‖xn-z‖+γ′n‖Tzn-z‖≤

α′n‖u-z‖+β′n‖xn-z‖+γ′n‖zn-z‖≤

(α′n+γ′nα"n)‖u-z‖+(βn+γ′nβ"n)‖xn-z‖+γ′nγ"n‖Txn-z‖≤

(α′n+γ′nα"n)‖u-z‖+(βn+γ′nβ"n+γ′nγ"n)‖xn-z‖≤M+‖xn-z‖.

由引理3可得

‖xn+1-z‖2=‖αn(u-z)+βn(xn-z)+γn(yn-z)‖2=

‖βn(xn-z)+γn(yn-z)‖2+2αn〈u-z,j(xn+1-z)〉≤

β2n‖xn-zn‖2+2βnγn‖xn-z‖‖yn-z‖+γ2n‖yn-z‖2+2αn〈u-z,j(xn+1-z)〉≤

β2n‖xn-zn‖2+2βnγn‖xn-z‖(M+‖xn-z‖)+γ2n(M+‖xn-z‖2)+

2αn〈u-z,j(xn+1-z)〉=

(βn+γn)2‖xn-z‖2+2γnM(βn+γn‖xn-z‖)+γ2nM2+2αn〈u-z,j(xn+1-z)〉=

(1-αn)2‖xn-z‖2+δn.

其中,δn=2γnM(βn+γn‖xn-z‖)+γ2nM2+2αn〈u-z,j(xn+1-z)〉.因此

注1本文引进了一个新的关于非扩张映像三重复合修正的Ishikawa迭代序列,并证明了该序列在一定条件下的强收敛性.显然，当α"n=0,β"n=1,γ"n=0时,即为文献[8]的结论;进一步,当α′n=0,β′n=1,γ′n=0时,即为文献[7]的结论.因此,本文所得的结果改进和推广了文献[7-9]等一些相关的近代结果.

[1]Kim T H,Xu Hongkun.Strong convergence of modified mann iteration[J].Nonlinear Anal,2005,61(2):51-60.

[2]Su Yongfu,Li Mengqin,Zhang Hong.New monotone hybrid algorithm for hemi-relatively nonexpansive mappings and maximal monotone operators[J].Appl Math Comput,2011,217(12):5458-5465.

[3]Wittmann R.Approximation of fixed point of nonexpansive mappings[J].Arch Math,1992,58(5):486-491.

[4]Lions P L.Approximation de points fixes de contractions[J].CR Acad Sci Ser A-B Paris,1977,284(21):1357-1359.

[5]Xu Hongkun.Iterative algorithms for nonlinear operators[J].J London Math Soc,2002,66(1):240-256.

[6]Ceng L C,Guu S M,Yao J C.A general composite iterative algorithm for nonexpansive mappings in Hilbert spaces[J].Comput Math Appl,2011,61(9):2447-2455.

[7]姚永红,陈汝栋,周海云.非扩张映像不动点的迭代算法[J].数学学报:中文版,2007,50(1):139-144.

[8]宣渭峰,王元恒.双复合修正的Ishikawa迭代逼近非扩张映像不动点[J].浙江师范大学学报:自然科学版,2009,32(4):381-386.

[9]傅湧.Hilbert 空间中非扩张映射Noor混合迭代序列的收敛性[J].浙江大学学报:理学版,2011,38(1):22-26.

[10]王元恒,曾六川.Banach空间中广义投影变形迭代法的收敛性[J].数学年刊:A,2009,30(1):55-62.

[11]王元恒,徐卫.非扩张映像不动点的一种变形迭代算法[J].浙江大学学报:理学版,2009,36(3):259-263.

[12]Xu Hongkun.An iterative approach to quadratic optimization[J].J Optim Theory Appl,2003,116(3):659-678.

(责任编辑陶立方)

StrongconvergenceofthetriplecompositemodifiedIshikawa′siterationfornonexpansivemappings

LUO Hongping, WANG Yuanheng

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

The strong convergence was established for the triple composite modified Ishikawa type iteration for nonexpansive mappings in Banach space with uniformly Gateaux differentiable norm. The results improved and extended the relevant results in other literatures.

uniformly Gateaux differentiable norm; nonexpansive mapping; triple composite modified Ishikawa′s iteration; strong convergence

O177.91

1001-5051(2013)01-0031-06

2012-10-08

国家自然科学基金资助项目(11071169)；浙江省自然科学基金资助项目(Y6100696)

罗红平(1987-)，女，浙江台州人，硕士研究生.研究方向：非线性泛函分析.

王元恒. E-mail: yhwang@zjnu.cn