非均质土坡降雨入渗的耦合过程及稳定性分析

李海亮，黄润秋，吴礼舟，方 正

（1.地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059；2.四川省交通运输厅交通勘察设计研究院，四川 成都 610059）

滑坡是一种在世界范围内普遍存在的地质灾害现象，降雨是其失稳的主要诱发因素［1］。降雨入渗坡体是一种典型的非饱和流固耦合现象［2］。要科学合理的分析评价边坡降雨入渗过程和稳定性，非饱和土流-固耦合是首先需要解决的重大问题。

在地质、环境因素等的作用下，土体大多呈现层状结构，形成层状土的原因有很多，但是都可将层状土分成2大类［3］:1)渗透系数较小的细质土覆盖渗透系数较大的粗质土；2)渗透系数较大的粗质土覆盖渗透系数较小的细质土。众多学者对降雨入渗和非饱和土流固耦合的问题进行了研究，Thomas(1997年)提出一考虑非饱和土变形的热、气、水运动耦合理论［4］；Wong(1998年)进行了非饱和土的固结耦合数值计算研究［5］；朱伟等［6］研究设计室内降雨入渗土柱试验，在初步揭示降雨入渗过程和规律的基础上，探讨准确反映降雨入渗量的有限元计算方法；詹良通等［7］建立了降雨入渗条件下无限长斜坡内水分运移模型，在合理简化的基础上得到了解析解；徐晗等［8］建立一个考虑水力渗透系数特征曲线、土-水特征曲线以及修正的Mohr-Coulomb破坏准则的非饱和土流固耦合有限元计算模型。同时，田东方等［9］、张晓咏等［10］、徐炎兵等［11］、吴礼舟等［12～13］在流固耦合数值分析和边坡稳定性问题方面也进行了研究。然而，大多数研究者假设边坡为均质的，对非均质边坡研究较少；或者采用了流固准耦合理论，并未真正实现流固的真耦合，这与实际情况是截然不同的，这可能导致研究的结果与实际情况产生偏差。在降雨条件下非均质边坡的入渗特性及变形等性状不同于均质边坡。本文拟在前人研究的基础上，通过数值分析方法，采用流固真耦合理论，以两种典型的双层层状土坡为例，分析非均质边坡在降雨条件下的入渗过程及稳定性，揭示了降雨诱发非均质土坡的变形破坏机制，并对一些影响因素进行分析，以期为研究多层土的降雨入渗以及更加准确地评价边坡稳定性提供借鉴。

1 流固耦合理论及强度折减法

1.1 非饱和土流-固耦合理论

土体渗流场和应力场之间是相互作用、相互影响的，其实质为应力场使土体发生变形，从而改变了介质渗透系数；渗流场的变化又会引起孔隙水压力分布的改变，使得渗流力和有效应力发生改变。本文采用的大型有限元软件ABAQUS可以对土中水的渗流和土体变形进行直接耦合分析。

根据虚功原理［14］，固相介质的应力平衡为:

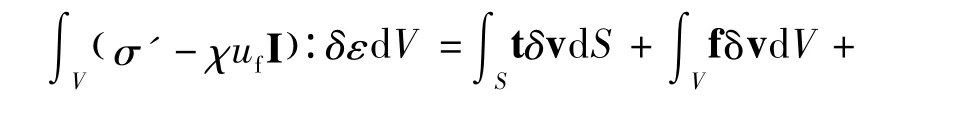
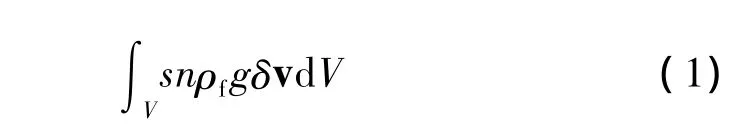
式中:δε——虚变形速率，δε=sym∂σv/∂()x；

σ'——有效应力；

δv——虚应变场；

t——单位面积的表面力；

f——单位体积的体积力(不含流体质量)；

s、n——固相材料的饱和度、孔隙率；

ρf——流体密度；

g——重力加速度。

用拉格朗日公式将虚功方程离散化得到固相材料的有限元网格，此时流体还需要满足连续方程:

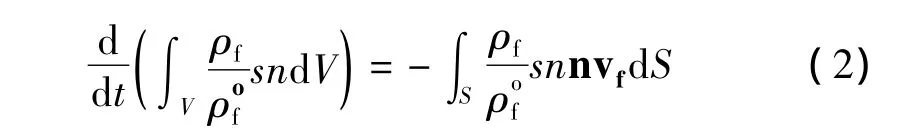
式中:vf——渗流速度；

n——S面外法线方向。

ABAQUS能将渗流场和应力场直接耦合，同时求解应力平衡与渗流连续性方程，并采用Newton迭代法求解方程。

1.2 有限元强度折减法的原理

1975年Zienkiewicz等首次提出了抗剪强度折减的概念。基于强度储备的概念可将稳定安全系数Fs定义为当土体材料的抗剪强度参数c和φ分别用其临界抗剪强度参数cf和φf所代替后，结构将处于临界破坏状态，其中:

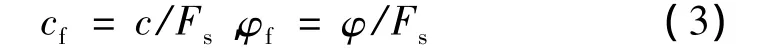
强度折减法的基本思想是在外荷载不变的情况下，将土体强度参数按式(3)进行折减，得到新的土体强度参数cf、φf进行分析，通过不断增加折减系数，直至土坡达到极限状态，此时的折减系数就是所要求解的边坡稳定性系数。

1.3 有限元强度折减法的失稳判据

弹塑性有限元强度折减法用于边坡失稳的判据大致可以分为三类:(1)有限元数值计算迭代的不收敛性；(2)特征部位(如坡顶、边坡内位移最大处等)位移(包括水平位移、竖向位移或总位移)发生突变；(3)广义塑性应变或等效塑性应变从坡脚到坡顶贯通。目前对每种失稳判据的有效性存在着不同的看法和解释。鉴于此，本文将根据特征部位位移发生突变并结合塑性区贯通作为失稳判据。

2 实验概况

为了深入讨论和研究非均质土坡在降雨条件下的入渗过程、规律和稳定性变化，本文建立了两种典型的非均质土质边坡模型，即粗-细型(上层为#2砂土，下层为#1砂土)和细-粗型(上层为#2砂土，下层为#3砂土)。为了进行对比分析，两种模型中上层土均为1m厚的#2砂土，下层分别为#1和#3砂土(厚度为1.5m)。土的物理力学参数如表1所示，边坡数值分析模型见图1，边坡坡比为1:1.5，AB、BC和CD段为降雨边界；DE段为排水边界，即当孔压为正时，假定流速与孔压成正比，孔压为负时，假定流速为零；AG和DE段固定水平方向的位移，EG段固定水平和竖直方向位移。L1、L2、L3和 L4为孔隙水压力监测剖面线。降雨强度考虑了20mm/h和10mm/h。

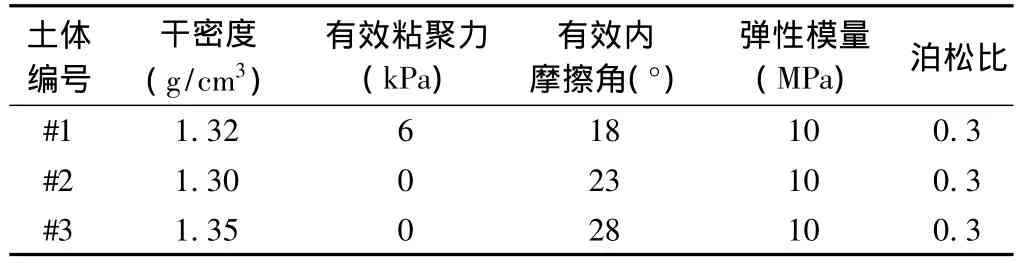
表1 土体的物理力学参数Table 1 Soil physical and mechanical properties

图1 边坡数值分析模型Fig.1 Numerical model of slope

渗透系数是非饱和土的重要参数之一，但是其变化范围很大且不易测量，而从土-水特征曲线能获取渗透系数，土-水特征曲线是非饱和土中体积含水量(饱和度)和吸力之间的关系曲线，非饱和土的行为特征与土-水特征曲线有密切关系。目前很多经验公式可以描述土-水特征曲线，本文采用应用很广泛的van Genuchten模型。模型表达式为:

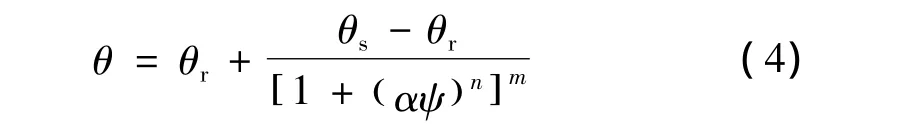
式中:θ——土的体积含水量；

ψ——压力水头(kPa)；

θs、θr——土的饱和、残余体积含水量；

α、n——经验拟合参数，m=1 －1/n。

非饱和土渗透系数表达式为:

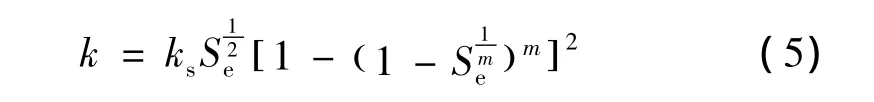
式中:k——非饱和土渗透系数；

ks——饱和土渗透系数；

Se——有效饱和度，Se=1/[1 +(αψ)n]m。

本次实验砂土的土－水特征曲线如图2所示，渗透系数如图3所示。

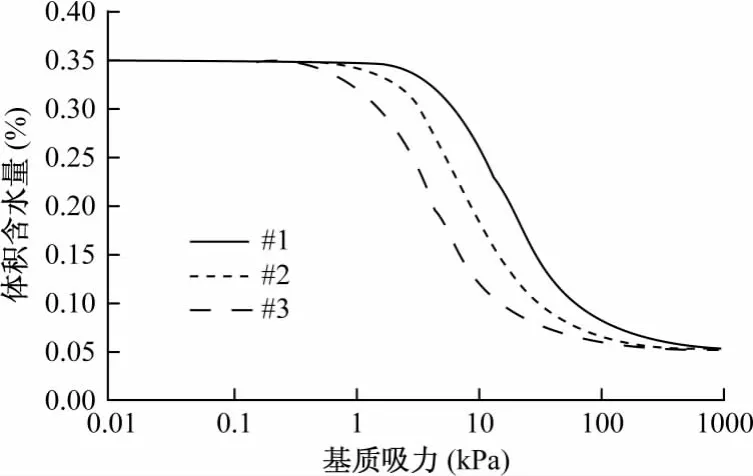
图2 土体的土－水特征曲线Fig.2 Soil-water characteristic curve of soils

图3 土体的渗透系数曲线Fig.3 Hydraulic conductivity curve of soils

为了得到较为实际的边坡初始条件，分析中假定整个坡体孔隙水压力为－20kPa，在无流量边界的条件下，运用ABAQUS的Geostatic分析步进行地应力平衡，平衡后边坡最大位移达到了10－8m，可以认为边坡达到了初始平衡状态。获取的边坡初始状态包括初始孔隙水压力、初始应力及饱和度等分布情况，可作为边坡降雨入渗暂态分析的初始条件。计算得出的渗流场见图4。

3 模拟结果与分析

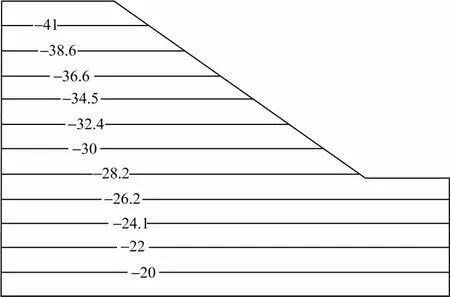
图4 初始时刻粗－细型边坡渗流场孔压等值线图(单位:kPa)Fig.4 Coarse-fine type slope pore water pressure isoclines of initial seepage(kPa)

图5为两种类型边坡在降雨强度10mm/h、历时12h、耦合情况下的孔隙水压力等值线图，相应的非耦合情况见图6。等值线图清晰地显示了整个土坡孔隙水压力的空间变化。耦合和非耦合情况下渗流场差异较大，主要原因是，考虑耦合作用时，应力场会导致土体渗透系数变小，所以降雨时耦合较非耦合入渗将会慢很多。因此，考虑耦合作用更符合实际情况。基于此，下面的分析将考虑非饱和渗流场和应力场的耦合作用。

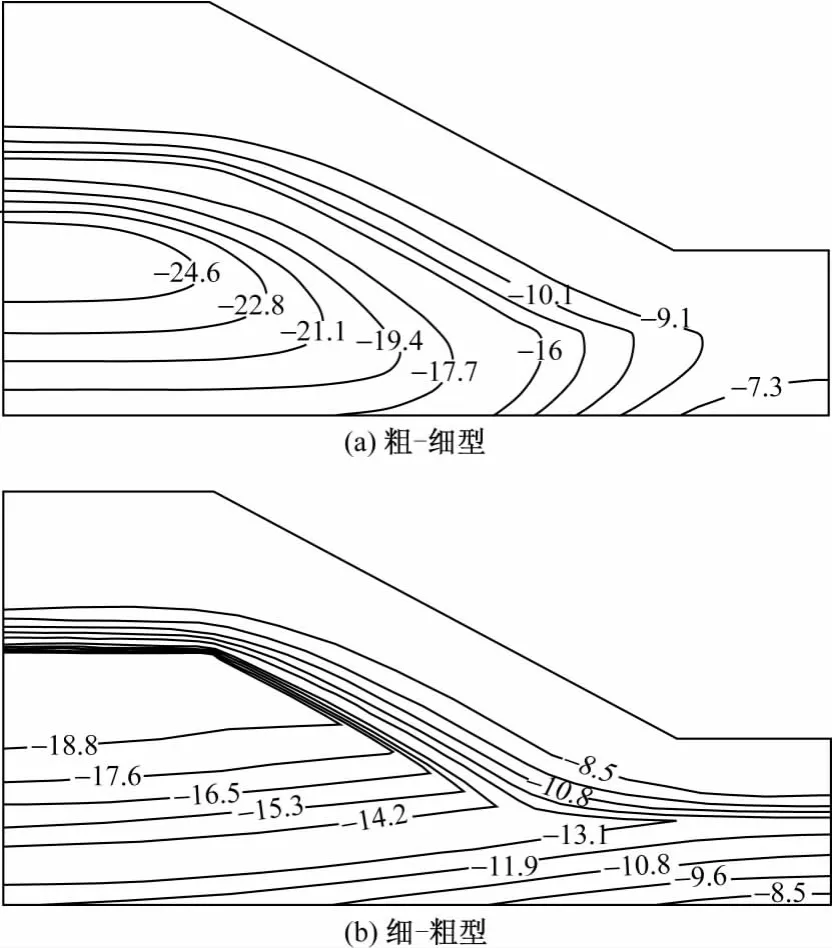
图5 降雨强度10mm/h、历时12h两种类型边坡耦合孔隙水压力等值线图(单位:kPa)Fig.5 Two type of slope isoclines of coupled pore water pressure with rainfall 12 hour and its intensity of 10 mm/h(kPa)

图7 降雨强度10mm/h时，不同时刻L2剖面线上两种类型边坡孔隙水压力－深度分布曲线Fig.7 Two type of slope pore water pressure-depth curve with rainfall intensity of 10 mm/h in profile L2

图7显示了降雨强度10mm/h时不同时刻L2剖面线上孔隙水压力pw随深度z的分布曲线。由等值线图可以看出，表层孔压变化很大，降雨约9h内，由孔压－深度分布曲线看出，下层土体孔压基本未发生变化，这说明雨水还未入渗到下层土体，随后，雨水入渗到下层土体，孔压不断增大，但是这种增大的趋势对于两种类型的非均质土坡并不一样。由此，降雨入渗过程可以分解为几个阶段。

对于细－粗型土坡，入渗过程可分解为2个过程:(1)雨水未进入到土层接触面，所有雨水均进入到土体中，并且只在上层土中渗流；(2)雨水入渗到下层土，由于下层土渗透系数大于上层土，因此在土层接触带处不会产生积水情况。这时下层土体孔压增大，沿深度呈近似线性分布，上层土体孔压增加速率明显减小。

对于粗－细型土坡，入渗过程将变得复杂一些，可以分解为3个过程:(1)这个过程与细－粗型土坡过程类似；(2)雨水进入到下层土，由于土体渗透系数变小，在土层接触面处将发生积水；(3)随着降雨进行，土层接触面发生积水后，积水面将不断向上迁移，最终将导致坡体表面积水。

3.1 降雨强度和时间对滑坡的影响

图8显示了降雨强度20mm/h时不同时刻L2剖面线上孔隙水压力pw随深度z的分布曲线。与图7对比分析发现，随着降雨强度的增大，雨水到达土层接触面的时间约为6h，提前了3h。上下层土体在接触面的孔压差值大大增加，将分别达到18kPa和20kPa，这将容易造成更大的塑性变形。

图8 降雨强度20mm/h时，不同时刻L2剖面线上孔隙水压力－深度分布曲线Fig.8 Two type of slope pore water pressure-depth curve with rainfall intensity of 20 mm/h in profile L2

3.2 稳定性分析

运用强度折减法对不同降雨强度和历时的边坡稳定性进行了计算，以坡体位移突变并结合塑性区贯通作为失稳判据。图9为粗-细型边坡降雨强度10mm/h的折减系数和水平位移的关系曲线，可以明显的看出不同降雨历时条件下，位移均存在突变点，位移突变的时间即为边坡破坏时刻。降雨强度10mm/h、历时12h的边坡，当折减系数为1.63时，等效塑性应变等值云图见图10，此时塑性区已经贯通到坡顶，已达到失稳的临界状态。综合分析位移突变曲线和塑性区贯通云图，确定边坡稳定性系数为1.63。由图10看出在两种土层接触面处产生了较大的塑性应变，随着变形不断变大，沿着接触面形成了滑动带。

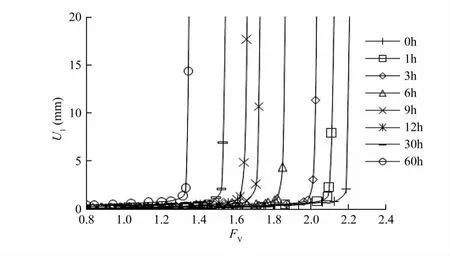
图9 折减系数-水平位移分布曲线Fig.9 Reduction factor-horizontal displacement curve

图10 等效塑性应变等值云图Fig.10 Nephogram of equivalent plastic strain

边坡稳定性系数随降雨强度和降雨历时的变化曲线见图11。两种典型非均质土坡稳定性系数均随降雨强度和历时增大而降低；降雨强度越大，稳定性系数降低越快；随后的降雨过程中，稳定性降低速率受降雨强度影响减小，而且曲线近于平行。

图11 两种类型边坡稳定性系数随时间变化曲线Fig.11 Two type of slope stability factortime curve

由图11可见，无论降雨强度多大，曲线均存在一个拐点。降雨强度为10mm/h时，曲线拐点横坐标为约9h；降雨强度为20mm/h时，曲线拐点横坐标为约6h。由前述可知，雨强为10mm/h，经过9h，雨水刚好进入到下层土体；同样，雨强为20mm/h，雨水入渗到下层土体的时间是6h。也就是说，雨水入渗到达下层土体时，边坡稳定性变化速率将减小。同时，粗-细型边坡相对细-粗型边坡受降雨影响较大，稳定性降低较快；随降雨时间增长，细-粗型边坡稳定性虽然在不断降低，但是变化较小。

图10显示滑带基本沿着两土层的接触面部分，为进一步分析降雨诱发非均质土坡变形失稳机制，选取粗-细型边坡，首先对抗剪强度参数c和φ折减1.63，然后进行雨强10mm/h、历时12h的降雨，降雨结束时，边坡稳定性系数为1。对图1的4条剖面线孔隙水压力进行分析(图12)。可见，降雨12h之后，孔隙水压力变化很大，同时4条曲线均存在一个突变，突变位置分别为:L1、L2在 z=1.0m，L3在 z=1.5m，L4在z=2.0m。不难发现，这4个剖面中，孔隙水压力突变位置均为土层接触面位置，也是土坡滑带所在位置。对于非均质土坡，土层接触面的位置容易产生孔隙水压力的突变，造成有效应力的迅速降低，使得土体产生较大的塑性变形，不断累进性变形之后便形成了滑带。

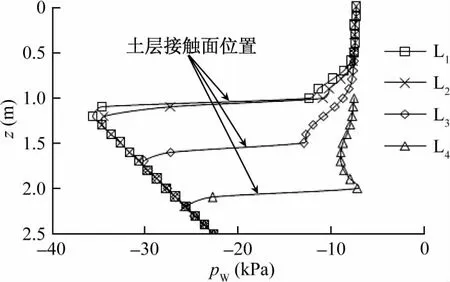
图12 不同剖面孔隙水压力-深度分布曲线Fig.12 Pore water pressure-depth curve of different profiles

3.3 渗透系数对滑坡的影响

以图1的粗-细型土质边坡模型为例，假设其他条件不变，将#1土体渗透系数取为2E-006m/s，以分析渗透性强弱对孔隙水压力和边坡稳定性的影响，不同渗透系数时的稳定性计算结果见图13。

图13 稳定性系数随时间变化曲线Fig.13 Slope stability factor-time curve

可见，在雨水未入渗到土层接触面时，底层土体渗透系数对边坡稳定性影响很小。当雨水到达接触面之后，稳定性系数降低速率随着#1土体的渗透系数变小而增大，这是因为下层土体渗透系数越小，接触带部位越容易积水，进而导致了稳定性系数降低更大。

4 结论

(1)运用流固真耦合理论分析降雨条件下的非均质土坡的渗流变形更符合实际。细-粗型土坡的降雨入渗过程分为2个阶段，粗-细型土质边坡的降雨入渗过程可以分为3个阶段。

(2)当雨水未入渗到底层土体时，稳定性下降很快，降低速率基本不变；当雨水入渗到下层土体时，边坡稳定性系数降低速率会变小；稳定性系数和时间分布曲线存在一个拐点，拐点的横坐标即为雨水到达土坡土层接触面时间。

(3)降雨诱发非均质土坡变形破坏机制具有特殊性，在土层接触带处，产生了较大的孔隙水压力突变，土体产生较大塑性变形，最终在接触面处形成滑带。

(4)雨水未到达土层接触面时，下层土体的渗透系数对边坡稳定性影响很小；到达之后，稳定系数降低速率随着下层土体的渗透系数变小而增大。

［1］王世梅.非饱和滑坡土体力学特性试验及其数值模拟［D］.武汉:武汉大学，2007.［WANG S M.Test and numerical simulation of the mechanical characteristics of the unsaturated Landslide［D］.Wuhan:WuHan University，2007］

［2］陈正汉，卢再有，朱元青.非饱和土的理论和实践［J］.力学与实践，2001，23(5):8-15.［CHEN Z H，LU Z Y， ZHU Y Q. Theory and practiceon unsaturated soils［J］.Mechanics and Engineering，2001，23(5):8 －15.(in Chinese)］

［3］韩同春，黄福明.双层结构土质边坡降雨入渗过程及稳定性分析［J］.浙江大学学报:工学版，2012，46(1):39 －45.［HAN T C，HUANG F M.Rainfall infiltration process and stability analysis of two-layerd slope［J］.Journal of Zhejiang University:Engineering Science，2012，46(1):39 －45.(in Chinese)］

［4］Thomas H R，He Y.Coupled heat-moisture transfer theory for deformable unsaturated soil and its algorithmic implementation［J］.International Journal for Numerical Methods in Engineering，1997，40(18):3421－3441.

［5］Wong T T，Fredlund D G，Krahn J.Numerical study of coupled consolidation in unsaturated soils［J］.Canadian Geotechnical Journal，1998，35(6):926 －937.

［6］朱伟，陈学东，钟小春.降雨入渗规律的实测与分析［J］.岩土力学，2006，27(11):1873 － 1879.［ZHU W，CHEN X D，ZHONG X C.Observation and analysis of rainfall infiltration［J］.Rock and Soil Mechanics，2006，27(11):1873 － 1879. (in Chinese)］

［7］詹良通，贾官伟，陈云敏.考虑土体非饱和特性的无限长斜坡降雨入渗解析解［J］.岩土工程学报，2010，32(8):1214 －1220.［ZHAN L T，JIA G W，CHEN Y Mc.Analytical solution for rainfall infiltration into infinite long slopes considering properties of unsaturated soil［J］.Chinese Journal of Geotechnical Engineering，2010，32(8):1214 －1220.(in Chinese)］

［8］徐晗，朱以文，蔡元奇，等.降雨入渗条件下非饱和土边坡稳定分析［J］.岩土力学，2005，26(12):1957－1962.［XU H，ZHU Y W，CAI Y Q，et al.Stability analysis of unsaturated soil slopes under rainfall infiltration［J］.Rock and Soil Mechanics，2006，27(11):1873－1879.(in Chinese)］

［9］田东方，刘德富，王世梅，等.土质边坡非饱和渗流场与应力场耦合数值分析［J］.岩土力学，2009，30(3):810－814.［TIAN D F，LIU D F，WANG S M，et al.Coupling numerical analysis of unsaturated seepage and stress fields for soil slope［J］.Rock and Soil Mechanics，2009，30(3):810 － 814.(in Chinese)］

［10］张晓咏，戴自航.应用ABAQUS程序进行渗流作用下边坡稳定分析［J］.岩石力学与工程学报，2010，29(1):2927－2934.［ZHANG X Y，DAI Z H.Analysis of slope stability under seepage by using ABAQUS program［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(1):2927 －2934.(in Chinese)］

［11］徐炎兵，韦昌富，李幻，等.非饱和土渗流与变形耦合问题的有限元分析［J］.岩土力学，2009，30(5):1490 － 1496.［XU Y B，WEI C F，LI H，et al.Finite element analysis of coupling seepage deformation in unsaturated soils［J］.Rock and Soil Mechanics，2009，30(5):1490 － 1496. (in Chinese)］

［12］Wu L.Z.，＆ Zhang L.M.Analytical solution to 1D coupled water infiltration and deformation in unsaturated soils.International Journal for Numerical and Analytical Methods in Geomechanics，2009，33(6):773－790.

［13］吴礼舟，黄润秋.非饱和土渗流－变形耦合的数值分析［J］.土木建筑与环境工程，2011，33(3):63－67.［WU L Z，HUANG R Q.Numerical analysis of seepage and deformation in unsaturated soil［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2011，33(3):63 －67.(in Chinese)］

［14］朱以文，蔡元奇，徐晗.ABAQUS与岩土工程分析［M］.香港:中国图书出版社，2005.［ZHU Y W，CAI Y Q， XU H. ABAQUS and geotechnical engineering analysis［M］.Hongkong:China Tushu Publishing House，2005.(in Chinese)］