一个概率问题的分析及模拟

易校尉，涂 平，陈 欣

(武汉工业学院数学与计算机学院，湖北武汉 430048)

1 问题介绍

目前算法分析领域的一个热点是利用随机化的方法求解一些特殊NP问题的近似解，这些随机算法的时间复杂度分析往往是比较困难的问题，一般着眼于计算或者是估计所给算法所需时间的数学期望。作者在一个问题的随机算法实践中曾遇到这样一个问题(类似的问题在遗传算法等随机搜索算法中经常出现):有四个数集:A、B、C、D，每次随机地从这四个数集的两个数集中选取两个数，如此重复多次，直至每个数集都至少有两个数被选取，求试验重复次数的数学期望。

为方便说明，可以把上面介绍的问题简化为:桌上有四个洞，每次抛两个球，这两个球随机地等可能地进入其中的两个洞(这两个球不能进同一个洞)，一旦发现每个洞内至少有两个球就不再抛球。问:平均要抛多少次球?

2 抛球次数的分布律

2.1 问题的初步分析及符号说明

设An表示事件:“前n－1次抛球后至少有一个洞内少于两个球，而第n次抛球后每个洞内至少有两个球”;Bn－1表示事件:“前 n－1次抛球后，有两个洞内各有一球，而其余两个洞内各至少有两个球”;Cn－1表示事件:“前 n－1次抛球后，有一个洞内有一球，而其余三个洞内各至少有两个球”

X为一随机变量，表示停止抛球后的抛球次数，所求的问题即为求EX。此外，注意到P{X=n}=P(An)，其中n＞3。由全概率公式，有

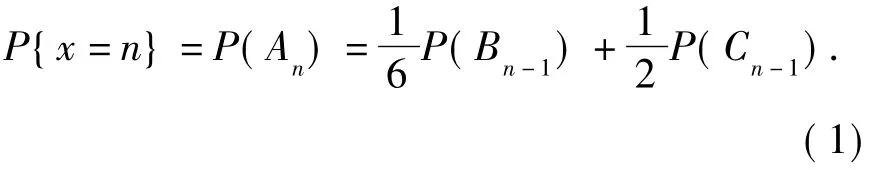
2.2 第一种情形的概率

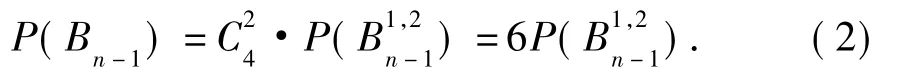
考虑到1号洞和2号洞的两个球有可能是同一次抛球入洞，也可能是在两次不同的抛球中入洞，由全概率公式有:

2.3 第二种情形的概率

首先注意，当n＜5时

设En－1表示事件“前n－1次抛球后，1号洞内恰有一球”。

由全概率公式，有

故由(8)及(12)有:当n＞4时，

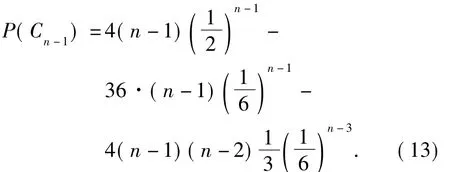
2.4 X 的分布律

由(1)、(5)及(7)有:

当 n＞4时，由(1)、(6)及(13)有:

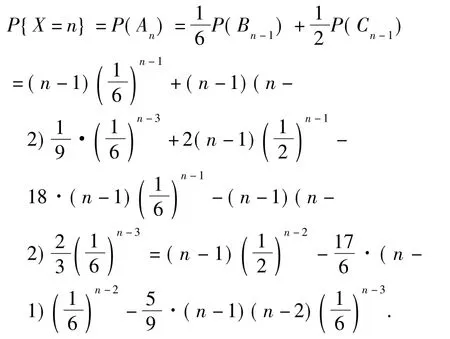
即:当n＞4时，

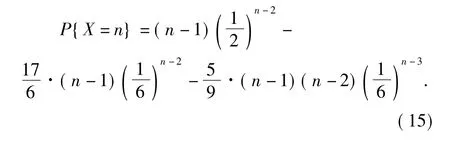
3 抛球次数的数学期望

3.1 要用到的几个级数

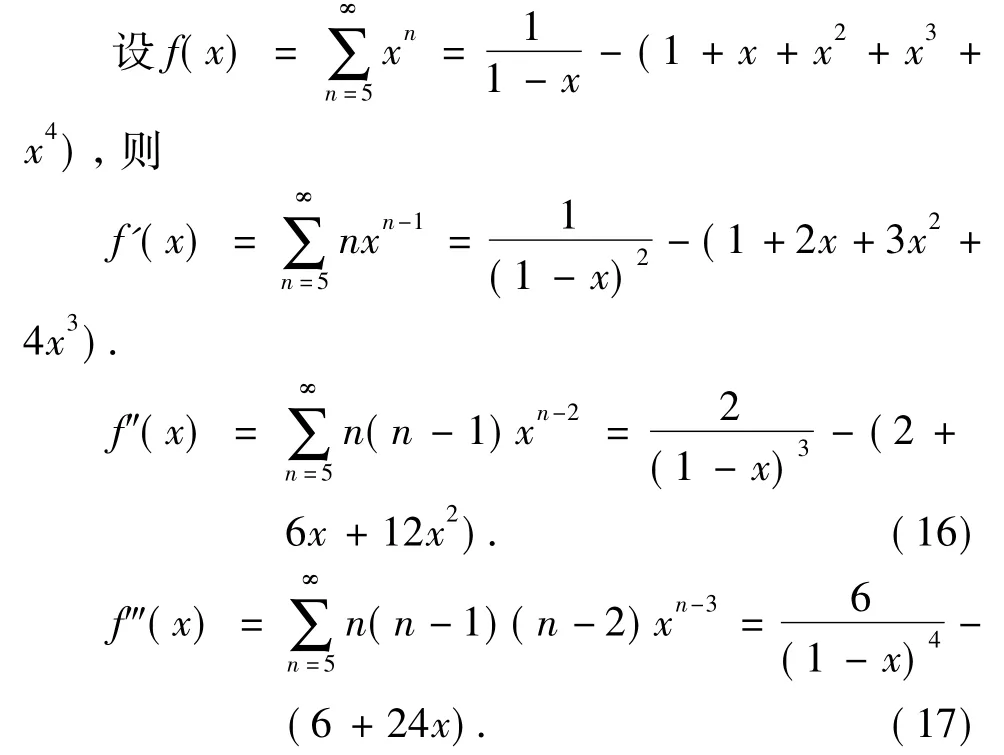
3.2 抛球次数数学期望的计算

由离散型随机变量的数学期望公式及(16)、(17)可知:抛球次数的数学期望为

4 计算机模拟算法及结果分析

上面的数学分析部分比较复杂，下面给出了多次重复试验所获得的抛球次数的平均值，由大数定理可知，当重复试验次数很大时，其平均值应十分接近所求得的数学期望。

模拟程序分以下几个模块。

模块一:tryt(int a［］)随机地抛两个球(两个进入不同的洞中)。

模块二:isok(int a［］)用于判断是否每个洞中至少有两个球。

模块三:countOfOkTry(int a［］)返回单次试验成功的抛球次数。

编制程序将该试验重复十万次，计算抛球次数的平均值为6.573780，与理论值6.5738十分接近。说明上面的数学分析部分是准确无误的。

5 问题的推广

利用所获得的抛球次数的分布律(14)、(15)式可以算得抛球次数的方差，该方差的计算并无本质困难，只是相对于数学期望的计算略为复杂而已，而且可以用计算机程序进行模拟以验证其正确性。

本文只讨论了4个洞，每次抛2个球的情形，可以进一步讨论m个洞，每次抛n个球的情形(其中n＜m)。这个一般问题到目前为止尚无一般结论，只能就特殊情形进行个别讨论。

［1］罗斯.应用随机过程——概率模型导论［M］.龚光鲁，译.北京:人民邮电出版社，2011.

［2］科曼.算法导论［M］.潘金贵，译.北京:机械工业出版社.2006.

［3］丁建立.遗传算法与蚂蚁算法的融合［J］.计算机研究与发展，2003(9).

［4］克努特.计算机程序设计艺术(第2卷)半数值算法［M］.苏运霖，译.北京:机械工业出版社，2008.

［5］格雷厄姆.具体数学［M］.北京:机械工业出版社，2007.