拉伸试验机柔度K值测定方法研究

韩永明，苏英群

（天津钢管集团股份有限公司，天津300301）

1 引言

在拉伸试验中，施加在试样上的载荷同样反向作用于试验机，使试验机的机架及夹持系统产生变形。试验机柔度K值就是使试验系统在承受载荷时，每增加单位载荷所产生的变形量。试验系统产生的变形不仅包括试验机机架的变形，而且包括加载机构、载荷测量装置、夹持装置、试样夹持等部分的变形。由于试验机柔度的影响，发生在试样的变形只是横梁位移的一小部分。拉伸试验机通常采用横梁位移速度控制，但是横梁位移的速度并不能代表试样的应变速率，两者通常会有非常大的差异。为了更加准确地测定金属材料的拉伸性能，使试验结果具有更好的重复性，随着试验机技术的不断进步，当前各国拉伸试验方法标准都提出了应变控制方法。但是由于应变控制方法对试验机和试样的要求很高，目前国内大部分拉伸试验机尚不能进行应变控制，位移控制方法还是目前拉伸试验机主要采用的控制方式。如果通过位移控制间接地控制应变和应力速率[1]，这就需要对试验机的柔度或刚度进行测定。传统的K值测定方法具有一定的局限性，需要使用具有屈服平台的试样进行测试，试验过程也比较复杂。随着试验机技术的不断发展，引伸计的广泛应用及数据处理软件的发展，系统K值可以更精确更方便地进行测定。本文中提出了速率法和能量法两种方法，结合Origin科学计算软件，可以准确方便地测定系统K值及绘制系统K值曲线。

2 试验机柔度K值的测量方法

2.1 速率法

由于试验机柔度的影响，横梁位移S应等于试样平行部分变形量ΔL与发生在系统上的变形之和，即：

式中：K为试验系统柔度，F为试样上的载荷。设试验从0时刻开始加载，横梁位移速度为V，试样平行长度为Lc，试样上的应变为ε，加载到t时刻时

横梁位移为：

则在任意时刻存在以下关系：

将上式变形，即得到柔度K的公式：

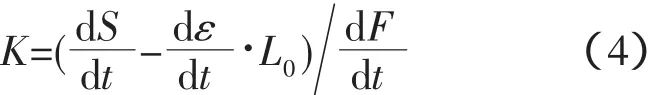
将公式（4）简化，可以得到：

公式（5）中，d（S-ε·L0）为瞬时拉伸试验系统的变形量增量，dF瞬时载荷增量，经计算即可得到的该时刻的K值。试验机的K值通常是非线性的，随试验加载过程不断变化，通过公式（5）即可以得到整个试验过程或某一试验阶段的试验机K值曲线。

以在意大利GALDABINI公司生产的SUN100电子万能材料试验机上进行的试验为例，试样为38.1 mm宽的条形试样，平行部分长度约为60 mm，采用标距为50 mm自动引伸计进行全程测量。试验后将采集的试验数据导入Origin 8.0进行数据分析，得到S-ε·L0和F两列数据并绘制曲线，见图1。图中右侧折点为最大力点，此后试样出现缩颈，载荷下降，试验系统变形也随之下降，直至断裂。取图1中曲线至最大力点的一段进行微分，即可以得到K值曲线（图2中K1曲线）。由于该试验机采用楔形夹头，试验开始阶段因夹持力逐渐上升，在200 kN载荷以下时K值呈下降趋势。在整个弹性变形阶段K值基本保持平稳，进入塑性变形阶段后，K值略有提高。在横梁速率进行切换时，因横梁位移速度突然提高，K值出现了波动。在趋近最大力时，K值也急剧提高，趋近于无穷大。将图2中弹性阶段的K值进行统计分析，得到其平均值为2.41×10-5mm/N，与文献1中测定该设备的K值平均值2.06×10-5mm/N非常接近。

对图1中弹性变形阶段曲线进行进行线性拟合，可以得到K值为2.22×10-5mm/N。

图3中曲线为在德国SCHENCK公司生产的RBO1600 拉伸试验机上所进行试验的（S-ε·L0）－F曲线。该试验机采用液压平推夹头，故与采用楔形夹头的试验机相比，弹性阶段K值线性更好。对这一阶段的数据进行线性拟合，得到该试验机的K值为 3.27×10-5mm/N。

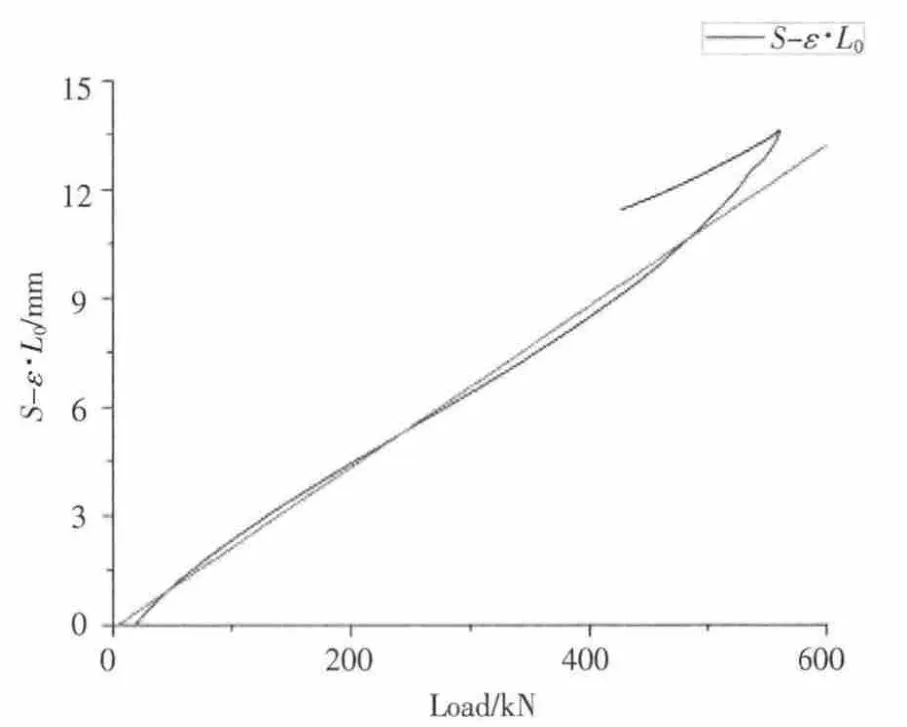
图1 对S U N 100拉伸试验机柔度曲线的线性拟合

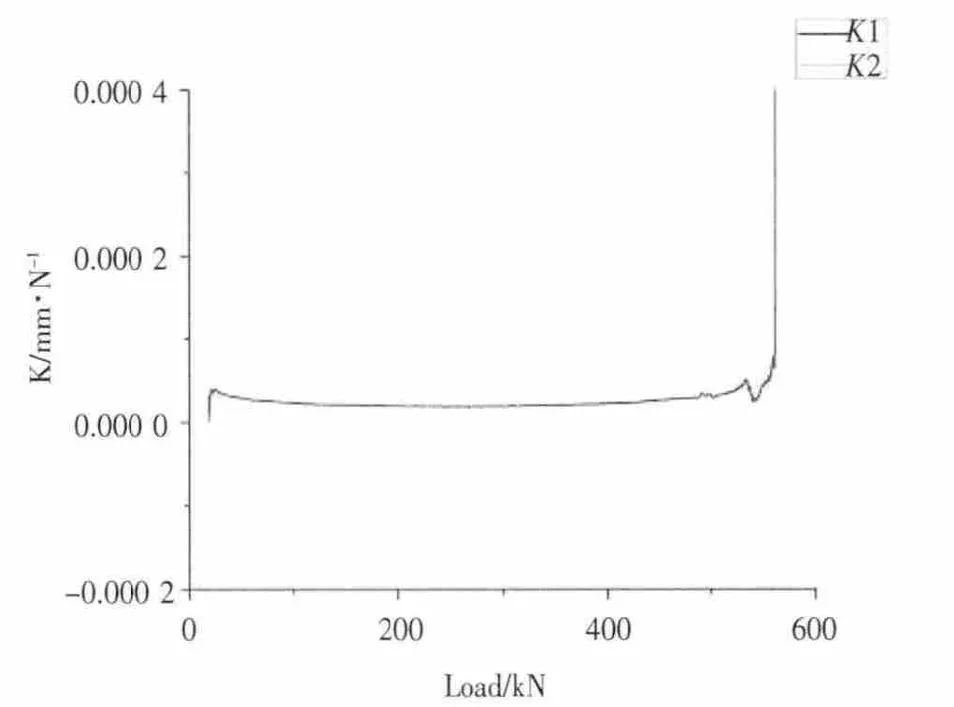
图2 能量法和速率法计算的K值曲线叠加图

图3 对R B O 1600拉伸试验机柔度曲线的线性拟合

2.2 能量法

现在从能量角度考虑试验机的柔度问题。如果试验机由理想的刚性材料制造而成，试验过程中完全不发生变形的话，试验机的位移就等于试样上变形量，试验中就完全没有能量损失，试验机所做的功全部被施加到试样上。然而，现实并非如此，试验中有很大一部分能量因为试验机自身的弹性变形消耗掉了。所以如果忽略因试样变形发热等原因造成的能量损耗，因试验机柔度影响消耗在试验系统中的能量W即等于整个试验系统所做的功减去试样变形所做的功，即：

式中：W1为消耗在整个试验系统（包括试样）上的总能量，W2为消耗在试样上的能量。

试验从开始加载到某一时刻时，消耗在整个试验系统（包括试样）上的总能量W1为：

而在同一加载过程中，因试样平行部分发生变形而消耗的能量W2为：

由公式（7）、（8）可知，我们可以绘制试验的载荷－位移与载荷－应变曲线，并对曲线进行积分即可得到试验中某一时刻的W1和W2。

因为试验系统能量消耗主要由机架等的弹性变形产生，所以因试验机柔度影响消耗在试验系统中的能量W可以写为：

式中：ΔL为试验系统的弹性变形。

对上式进行微分，得：

即：

即在试验的任意时刻，W-F曲线的斜率即为该时刻系统柔度与载荷的乘积。求出该斜率，除以该时刻的载荷，即可以得到该时刻试验机的柔度K值。

利用Origin 8.0分别对2.1中试验的载荷－位移与载荷－应变曲线进行积分，求得其曲线下的面积，即其所做的功。根据公式（7）和公式（8）计算出W1、W2两列数据，两列数据相减即得到W，图4为绘制的W－F曲线，图中A点为弹性阶段结束点，B点为最大力点。从开始加载开始，消耗在试验系统中的能量随载荷的增加而增加，在最大力处达到最大值，然后随载荷下降而逐步释放能量直至试样断裂。

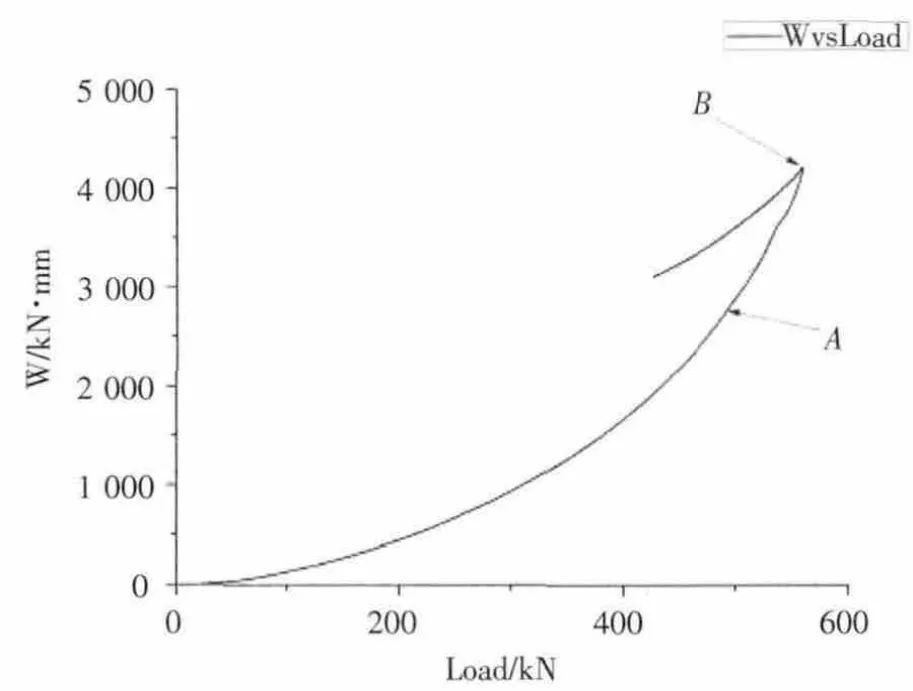
图4 W－F曲线

对图4中的W－F曲线进行微分，得到曲线的斜率，即dW，根据式（11）即可计算K值，图2为d F绘制的能量法和速率法计算的K值曲线叠加图，K1为速率法计算的K值曲线，K2为能量法计算的K值曲线，两条曲线完全吻合，证明两种方法没有实质上的差别。经计算弹性阶段的K值平均值为2.41×10-5mm/N，与速率法计算的结果完全相同。

如对图4中原点至点A的弹性段曲线进行多项式拟合（见图5），由于试验条件的原因，例如试验前加载预载荷等，试验在很多情况下载荷、位移可能并非从零点开始

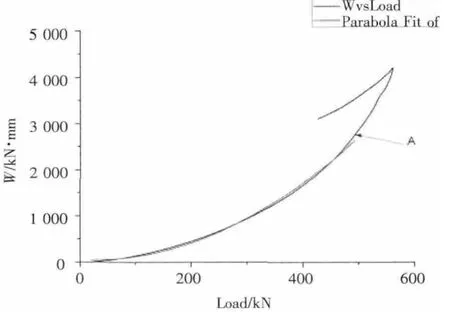
图5 对W－F曲线中弹性变形部分的2次多项式拟合

式（9）可以改写为：

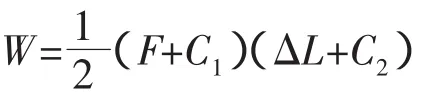
即：

式中：C1、C2为修正系数。

由公式（12）可知，对W-F曲线的如弹性阶段进行2次多项式拟合，可取二次项系数的2倍，作为弹性阶段的试验机平均柔度。由Origin对曲线进行二项式拟合，计算出弹性阶段试验机柔度K值为2.35×10-5mm/N，与采用前面计算的K值相当接近。

3 注意事项

在对曲线进行微分计算以确定斜率时，如曲线锯齿状比较严重的话，会严重影响计算精度。因此在必要时可以对曲线进行平滑处理，以保证微分结果具有较小的离散度。

两种方法均使用引伸计测量标距内变形量计算应变，建议引伸计标距应尽量接近试样平行长度，以减小测量误差。

K值的测定结果会因试验条件的不同而产生较大的离散性，故建议采用多次试验的方法确定K值的平均值。

4 结果与讨论

对于同一试样两种方法的K值分析结果非常接近，曲线完全重合，且由公式（6）、（7）、（8）、（11）经推导可以得出公式（5），证明两种方法并无实际差别，只是分析问题的角度不同。从能量角度看，我们忽略了试验过程中试样发热、摩擦等能量损失，在弹性阶段这些能量损失很小，在进入屈服之后，尤其是试样出现缩颈后，能量损失加剧，此时K值的计算会与实际情况有较大的偏差。当载荷接近最大力时，dF趋近于零，所以K值的计算结果趋近于无穷大。

采用楔形夹头的试验机的K值在试验弹性变形阶段因夹持载荷逐渐增大而呈非线性，而采用液压平推夹头的试验机的K值在弹性变形阶段基本呈线性。

建议采用线性或二次多项式拟合的方法，可以准确快速地计算出K值。

[1]苏英群．拉伸试验全程位移控制研究[J].冶金分析，2008（增刊2）：1622-1626.