基于PCA 的BP 神经网络在城市供水预测中的应用
2013-10-22李凌霄
肖 汉,曹 军,李凌霄
(山东水利职业学院,山东日照 276826)
近年来,我国许多城市给水系统的供需矛盾日趋突出,城市水量紧缺的现象越来越普遍。准确的城市供水量预测不仅可为水资源分配、水厂建设和扩建以及选址提供重要的科学依据,也是城市供水系统优化调度的重要基础。目前城市供水量预测的主要方法有长期趋势分析法、回归分析法、三角函数预测法、灰色预测法、季节指数平滑法和神经网络法等[1]。由于给水系统的复杂性,城市供水量不仅受当地水资源总量的影响,而且还与城市的经济发展、人均生活水平、供水设施建设、供水价格以及境外引水等众多因素有关。因此,目前尚不存在公认的普适性预测模型。实际工作中,无论采用何种预测模型,都需要大量的基础资料和筛选影响因子,这也是预测模型的关键和难点所在。首先,人们往往很难全面认识和描述供水系统中各变量间的相互关系,特别是变量间的非线性函数关系;其次,建立供水预测模型所需的大量基础统计资料也常常十分缺乏,并且与之对应的,供水量影响因子选择过少,必然会影响预测结果的准确性,而因子过多,会使网络训练复杂化,可能陷入局部优化问题,难以得到全局优化解[2]。
BP 神经网络是利用非线性可微分形式进行权值训练的多层网络,是神经网络理论中最为精华的部分,并具有较强的独立性和灵活性,尤其是对于处理复杂性系统有着先天的优越性。本文着眼于通过主成分分析(Principle Component Analysis,PCA)去掉BP 神经网络输入样本的冗余属性,消除网络输入之间的相关性,以筛选后的因子集合为输入指标,降低网络的神经元数,进而提高模型的学习与泛化能力[3]。
1 预测原理
1.1 PCA
PCA 是将多个变量通过线性变换以选出少数重要变量的一种多元统计分析方法。其基本思想是通过变量的相关系数矩阵内部结构的研究,找出能控制所有变量的少数几个随机变量去描述多个变量直接的相关关系。从数学角度而言,这属于降维处理技术[4]。
PCA 的一般步骤为:
(1)数据的标准化处理

其中i=1,2,…,n,n为样本点数。j=1,2,…,p,p为样本原变量数目。
(2)计算数据[xij]n×p的协方差矩阵R。

(3)求R 的前m个特征值:λ1≥λ2≥λ3≥…≥λm,以及对应的特征向量u1,u2,…,um,它们标准正交。
(4)计算累计方差贡献率Q。

(5)求m个变量的因子载荷矩阵。

1.2 BP 神经网络
BP 神经网络是目前应用最广泛的一种神经网络模型。BP 算法的基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传入,经各隐含层逐层处理后,传向输出层。若输出层的实际输出与期望的输出不符,则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐含层向输入层逐层反传,并将误差分摊各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程,是周而复始地进行的。权值不断调整的过程,也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可接受的程度,或进行到预先设定的学习次数为止[5]。其学习算法过程如下:
(1)初始化。给每个连接权值wij、vjt,阈值θj和γj赋予空间(-1,1)内的随机值。
(2)随机选取一组输入Xk=(x1,x2,…,xn)T和目标样本Dk=(d1,d2,…,dp)T提供给网络。
(3)计算隐含层各单元的输入与输出。

(4)计算隐含层各单元的输入与输出。

(5)计算各层各单元一般化误差。

(6)修正连接权vjt和阈值γj。

其中α为学习速率,取值0<α<1。
修正连接权wij和阈值θj。
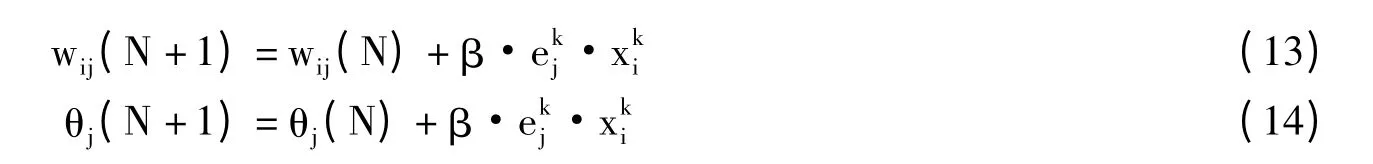
反复(2)~(6)步骤直到样本训练完毕。
反复(2)~(7)步骤直到满足精度[6]。
2 应用实例
2.1 确定供水量主要影响因子
选取抚顺市市区1991~2008年供水量序列资料和社会经济资料作为基础数据(部分统计结果见表1)。选取GDP、人口、工业总产值、建成区土地面积、用电总量、园林绿地面积和土地面积等7个变量,应用SPSS 软件的主成分分析,求得相关系数矩阵,结果见表2。从表2 可知,7个因子存在不同程度的相关性。其中,GDP 与工业产值的相关性最高,相关系数为0.99,工业产值与用电总量相关性次之,为0.924。由此可提取出彼此独立的变量,筛选有代表性的因了构造BP 神经网络的输入样本。

表1 抚顺市辖区典型年供水量及社会经济统计表Table1 Water supply & social economy statistics of Fushun city area

表2 相关矩阵Table 2 Correlation matrix

表3 主成分特征值和贡献率Table 3 Eigenvalues and contribution rates of principle constituents
表3 中,可以看出,第一因子的贡献率为76.671%,前2个因子的累计贡献率达91.772%,由此表明前2个因子代表了源数据7个变量90%以上的信息,其中第一个公共因子的代表性最强,第二个次之,以此类推。因此可以确定由前两个因子代替所选的七个因子。
由表4 可以看出,GDP、建成区土地面积、工业产值对因子1 的荷载都超过了0.95,相对其他因子贡献较大;人口对因子2 贡献最大。因此,选GDP、建成区土地面积、工业产值和人口4个变量作主成分,并以此构造BP 神经网络的输入样本。

表4 因子载荷矩阵Table 4 Component matrix
2.2 构建BP 神经网络
2.2.1 建立网络模型 根据PCA 的结果,本文选取GDP、建成区土地面积、工业产值和人口四个影响因子为输入变量,即一个4 维向量。目标向量就是预测当年的供水量,即输出变量为1 维向量。网络隐含层和输出层均采用S 型函数。这是由于函数的输出位于区间[0,1]中,正好满足网络输出的要求。从样本数据中选取1991~2004年样本进行网络训练,2005~2008年的已知样本对网络进行检验。期望误差取0.01,运算次数11000,学习率为0.75。
2.2.2 预测结果为了能找到比较合理的隐含层神经元数,建立了3~13个隐含层神经元的BP 网络结构,通过比较运行结果,选出较合适的神经元数为6。因此网络的拓扑结构为4:6:1,预测值与实际值对比结果见图1。训练结果进行样本检验,检验结果及检验误差见表5。

表5 供水量预测检测结果Table 5 Testing outcome of total water supply prediction
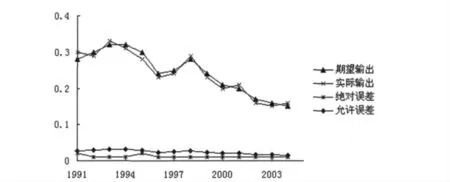
图1 BP 神经网络预测结果分析图Fig.1 Prediction outcome of BP neutral networks
由预测数据与原始数据的分析来看,期望输出与实际输出曲线拟合度较高,样本绝对误差均小于允许误差,满足精度的要求。检验样本2005~2008年实际需水量与计算需水量之间的相对误差分别为4.1%、7.5%、8.5%和8.9%,2007年和2008年期望输出与实际输出存在较大误差,其主要原因是模型参数选择时所依据的样本系列尚不能代表总体,再有BP 神经网络模型输入层节点数、隐层节点数、节点转换函数类型、模型训练方式等都会对模型的模拟精度产生影响。
3 结语
(1)本文运用PCA 与BP 神经网络模型相结合的方法,以抚顺市为例,进行供水量预测,为完善区域水资源信息系统,优化水资源配置,有效解决区域水资源供需矛盾提供了参考依据。
(2)运用PCA 分析的方法对原始数据进行预处理,提出4个主成分,即GDP、建成区土地面积、工业产值和人口。GDP、建成区土地面积、工业产值对因子1 的荷载都超过了0.95;人口对因子2 贡献最大。因子1和2 的累计贡献率达91.772%。
(3)由于神经网络模型具有局部逼近的特征和较强的非线性映射能力,因此它能够较好地模拟具有较强非线性变化特点的供水预测问题。基于PCA 的BP 神经网络简化了网络输入样本,消除了网络输入之间的相关性,加快了网络的收敛速度。最终取得了良好的预测结果。
(4)随着预测时间的延续,模型所得预测值不可能完全符合今后的实际情况。鉴于此,可考虑将今后每年所得到的新数据加入到变量样本中重新建立主成分进行预测。
[1]赵 凌,张 健,陈 涛.基于ARIMA 的乘积季节模型在城市供水量预测中的应用[J].水资源与水工程学报,2011,22(1):58-60
[2]李适宇,厉红梅,林亲铁.深圳市供水最BP 种经网络预测[J].给水排水,2004,30(12):105-107
[3]龙训建,钱 鞠,梁 川.基于主成分分析的BP 神经网络及其在需水预测中的应用[J].成都理工大学学报(自然科学版),2010,37(2):206-210
[4]余建英,何旭宏.数据统计分析与SPSS 应用[M].北京:人民邮电出版社,2003.291-310
[5]杨建刚.人工神经网络实用教程[M].杭州:浙江大学出版社,2003.44-45
[6]倪红珍,贾传义,王 浩,等.智能网络化水资源的实时预测分析[J].山东农业大学学报(自然科学版),2004,35(2):231-237
