三维激光扫描系统在建立单株立木材积模型中的研究

赵 芳，韦雪花，高 祥，刘晓丽，冯仲科

(北京林业大学 测绘与3S 技术研究中心)

目前量测森林蓄积量的方法多种多样，如何科学、精确、精确、高效的量算森林蓄积量是目前发展的主要趋势。由于直接测定立木材积比较困难，所以许多科学家也研究出了许多种测树仪器和方法。例如圆筒测高器、布鲁莱斯测高器等，对测树学的研究和发展起到了一定的推动作用。虽然方法很多，但仍还存在测量项目单一，精度不高等特点。三维激光扫描技术应用于森林蓄积量测定，将比传统方法省时、省力，节约经费。由于三维测量系统具有实时性、高精度、非接触性和机动性等特点，利用三维激光扫描技术进行森林蓄积量测定必将是未来数字化林业测量技术的发展趋势［1］。

1 量测森林蓄积量的研究和方法现状

解析木计算法需要伐倒树木，然后对其进行实测计算。虽然用此方法计算得到的结果比较精确，但是往往需要对测区内的待测树木伐倒，再对其进行量测胸径、树高等参数，逐步计算该树木的精确材积，这样严重破坏树木及森林的生长。立木计算法主要有每木检尺、角规测树、全站仪测树和临时样地调查等几种。为了取得科学、精确、可靠的数据，往往需要在野外选取大批的样地林木(标准木)，人工量测其胸径、树高、冠幅等参数。这些方法不仅作业周期长、工作效率低、劳动强度大、费用高、环境恶劣，而且测量精度也无法得到保证。

近几年芬兰的尤耶尔维开始研究基于图像测量技术的树径测量方法，利用数码相机或CCD 摄像机摄取树木及置于其旁边的校准标尺的图像，再根据几何比例关系用相应方法得出树干直径和树高;澳大利亚的奥斯汀提出利用空中雷达进行数据分析和处理，计算立木蓄积量;目前还有一种先进的方法，就是是利用3S 技术，结合少量地面样地调查数据，建立待测区域内的以样地大小为单位的森林蓄积量估测方程，以此减轻地面工作量。但此方法受林冠影响，难以获取树高、直径等重要的测树因子，估测误差较大，且费用高。

为了能够较好地避免上述森林蓄积量测定方法的不足，本文提出一种基于激光扫描的测树方法。与传统方法相比，该方法扫描材积测定误差小、工作效率高、不破坏生长期的树木，适于林区在线作业。

2 研究区域

本研究的外业数据采用地面三维激光扫描系统对单木进行扫描，研究区为位于北京市海淀区西北部苏家坨镇境内的鹫峰森林公园林场，北纬39°54'，东经116°28'，森林覆盖率已达96.4%，横跨海淀和门头沟两个区，面积832.04 hm2，共划分为6 大经营区，15个林班，106个小班。林区内主要有油松、华山松、龙爪槐、银杏、栎树、侧柏等树型。本次研究从中选择了6 块样地，在其中挑选出三个树种(油松、龙爪槐、银杏)，共180株标准木来进行研究。

3 利用三维激光扫描技术计算材积

3.1 三维激光扫描系统原理

三维激光扫描系统主要由扫描仪装置、控制器(计算机)和电源供应系统三部分组成。其工作目标就是快速、方便、准确地获取近距离静态物体的空间三维模型，以便对模型进行进一步地分析和数据处理［2］。三维激光扫描成像系统的工作过程，实际上就是一个不断重复的数据采集和处理过程，它通过具有一定分辨率的空间点(x，y，z)(其坐标系是一个与扫描仪设置位置和扫描仪姿态有关的仪器坐标系所组成的点云图)来表达系统对目标物体表面的采样结果［3］.

单桩嵌岩工艺1的具体流程如图1所示。首先通过单桩自沉如泥、桩锤沉桩，将单桩打至岩层表面；其次，在单桩内部下钻机，缩孔钻至设计底标高处；最后，将钻机提出，用桩锤继续讲单桩沉桩至指定标高。

三维激光扫描系统的原始观测数据主要是:

①两个连续转动的用来反射脉冲激光的反射镜的角度值，即水平方向值α和垂直距值θ;

②通过脉冲激光传播的时间计算得到的仪器到扫描点的距离值S ;③扫描点的反射强度。数据(α，θ，S)用来计算扫描点的三维坐标值，扫描点的反射强度用来给反射点匹配颜色。基于(α，θ，S)3 种数据可求得扫描点的三维坐标。

距离S 一般由检测激光脉冲从发出到接收之间的时间延迟计算获得。设发射脉冲往返时间间隔为tl，目标点p 与扫描仪距离S为:S=12 Ctl，C为光速［1］［4］。(图1)

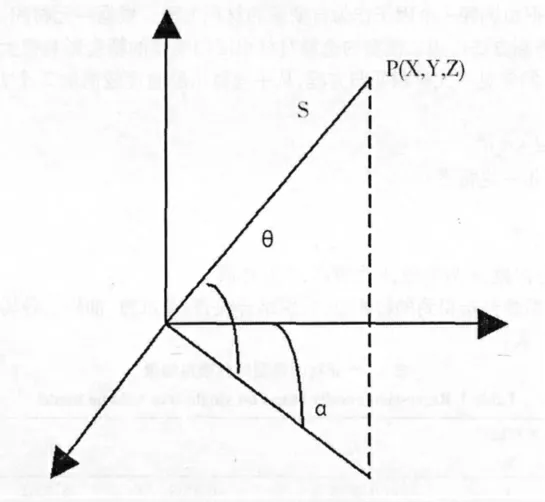
图1 激光扫描三维测量原理Fig.1 The principal of three dimensional laser scanner

3.2 利用三维激光扫描系统量测立木材积

首先根据待扫描树木的位置、大小形态和需要获取的控制点设计各扫描站和控制标靶的位置。然后启动扫描仪，对目标立木进行扫描。最后利用Cyclone 软件提供的丰富的点云数据处理功能，通过选取、截取、围栏选定的点云数据匹配生成面和复杂形体表面的不规则三角网，建成立木的三维树干表面模型［2］。

根据所建的三维树干表面模型，使用圆柱和圆台体模拟树干，把根据胸径的一定径阶把树干模拟分成若干个圆柱和圆台，然后利用Cyclone 提供的计算功能计算出模拟树干的表面积，从而计算出该立木的材积。此方法适合树干形状较接近圆柱或圆台的标准木计算材积。

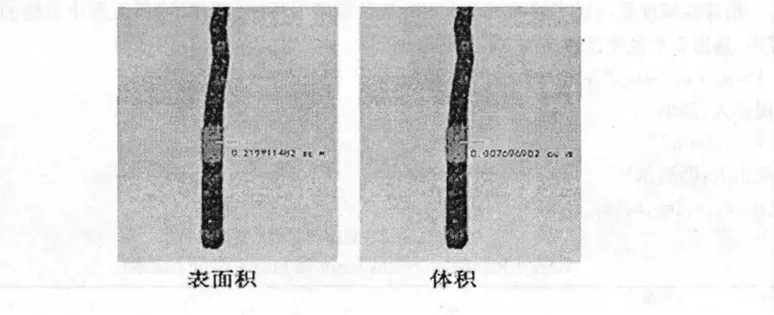
图2 使用圆柱和圆台体模拟树干求树干表面积与体积Fig.2 Calculating the exterior area and volume of trunk by trunk simulation based on cylinder and frustum of a cone

4 建立材积回归模型

根据三维激光扫描系统所得到的点云信息，得到每株样木的树高、胸径等参数因子和模拟的三维树干表面模型计算出的材积建立相关关系，分别建立了一元材积回归方程、二元材积回归方程。

4.1 建立一元材积回归模型

一元材积方程是根据由胸径一个因子作为自变量的材积方程。根据一元材积方程计算森林蓄积量方法简单，在森林普查中得到方法应用。模型的选择对材积回归模型的精度影响很大，所以根据孟宪宇编写《测树学》第五章中总结的常见一元材积回归方程，从中选择出经验度较高的2个方程来建立回归材积模型:

(1)V=a0+a2+a2d+a2d2

(提出人:覆赫纳德尔－克雷恩)

(2)V=A0Da1

(提出人:伯克霍特)

式中:a0，a1，a2均为常数，d为胸径，h为树高，V为材积。

根据三维激光扫描系统分析得到的材积量，分别结合银杏、龙爪槐、油松三种树种的胸径，回归得到一元材积模型，各参数如下表:

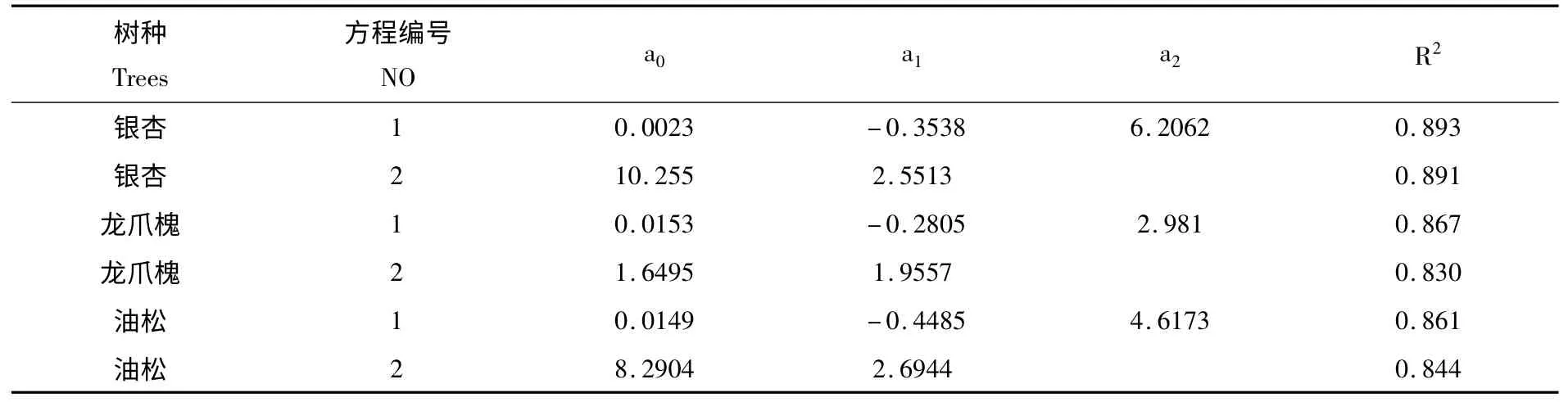
表1 一元材积模型回归模拟结果Table 1 Regression results based on single tree volume model

由上表可以看出，以上各个模型的相关系数都在0.83 以上，拟合精度较高。对3个树种的方程1和方程2 分别进行比较，可见方程1 较优于方程2，拟合精度方程1 较高。

4.2 建立二元材积回归模型

二元材积方程是根据由胸径、树高二个因子作为自变量的材积方程。在建立单木材积模型时，仅参考胸径这一指标在精度是远远不够的。本次实验从孟宪宇编写的《测树学》第五章中总结的常见的二元材积方程中，选出2个经验度较高的方程来进行回归:

1.V=a0+a1d+a2d2+a3dh+a4d2h+a5h

(提出人:迈耶)

2.V=a0(d2h)a1

(提出人:斯泊尔)

式中:a0，a1，a2，a3，a4，a5均为常数，d为胸径，h为树高，V为材积。

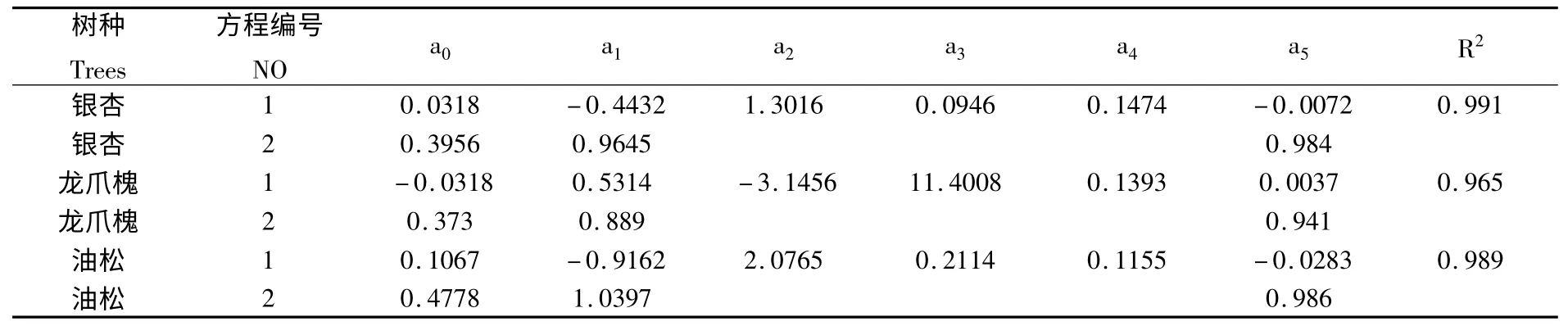
表2 二元材积模型回归模拟结果Table 2 Regression results based on binary volume model

从以上两表(表1、表2)的R2指标来看，表2 中的二元材积模型能取得较好的拟合效果，相关指数都达到0.98 且很接近。

4.3 适应性检验

模型的拟合精度检验不仅仅是在建模单元范围内满足既定精度要求，还需要通过对模型在应用中产生的最大偏差进行检验，验证是否在精度范围之内［5］。

对上述回归得到的3个树种的6个一元材积模型和6个二元材积模型进行拟合精度检验，分别计算其系统误差(表示每个样本单元实际值与其相应的模型估计值的相对误差的平均水平，是衡量材积模型精度高低的一个常用指标)、平均误差(表示各样本单元实际值与其相应的模型估计值的相对误差绝对平均数，它排除了样本单元间正负误差的相互抵消，反映的是用胸径和树高估计单株材积的误差平均水平)和均方误，计算检验结果如下表(表3、表4)［6］:

表3 一元材积表回归标准差计算Table 3 Regression standard deviation based on single tree volume table %

表4 二元材积表回归标准差计算Table 4 Regression standard deviation based on binary volume table %

由上表可以看出，以上一元材积模型的系统误差在 ±2.5～±4.1 之间，平均误差最小的为银杏的两个模型3.25和－3.23，二元材积模型的系统误差在±2.2～±3.6 之间，平均误差最小的也为银杏的两个模型－1.97和2.15。由此数据可见，对3个树种的方程1和方程2 分别进行比较，可见方程1 较优于方程2，拟合精度方程1 较高。也就是说在本样地内的银杏采用回归方程V=a0+a1d +a2d2+a3dh +a4d2h+a5h 拟合精度较高。

5 算例与分析

在建立材积模型初期，3 各树种各预留10 棵立木作为检验木。采用同样方法，利用激光扫描仪得到该立木的胸径d、树高h 及模拟树干表面模型计算出的材积，把此材积V 近似的看做真值。然后结合上述回归到的一元回归模型和二元回归模型，推算出其材积V’。比较结果如下各表(表5－表10):

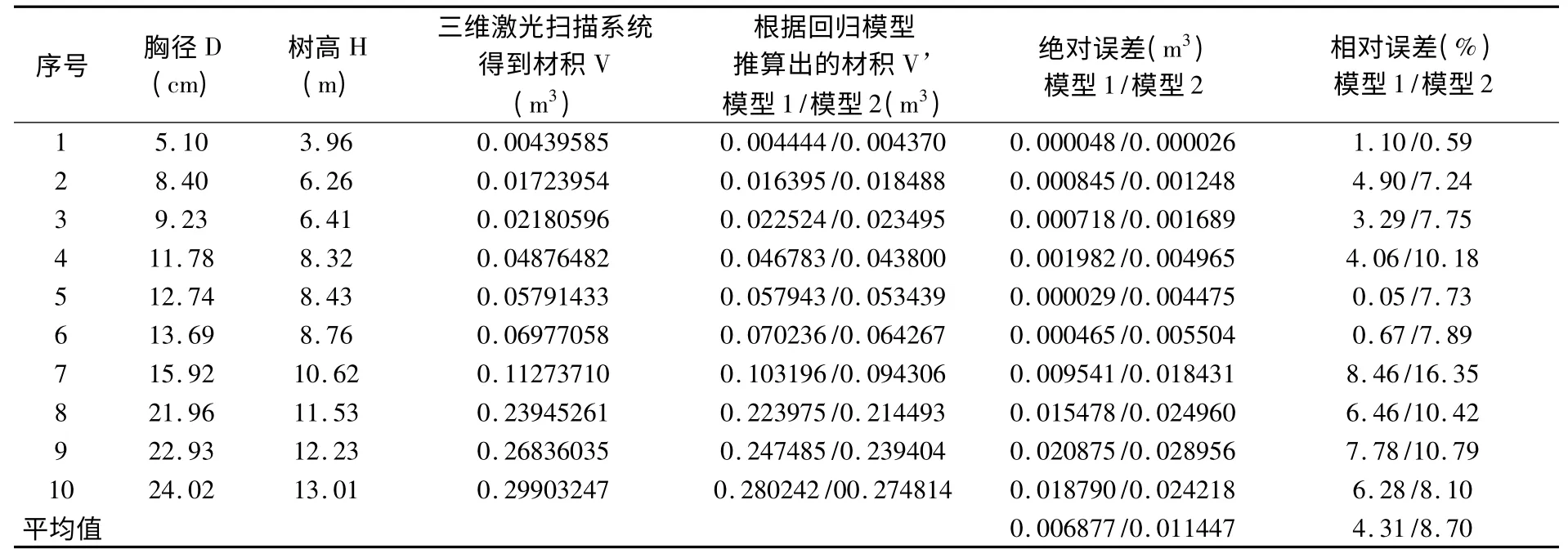
表5 银杏一元材积回归模型绝对误差和相对误差Table 5 The absolute error and relative error of single tree volume model for Gingko

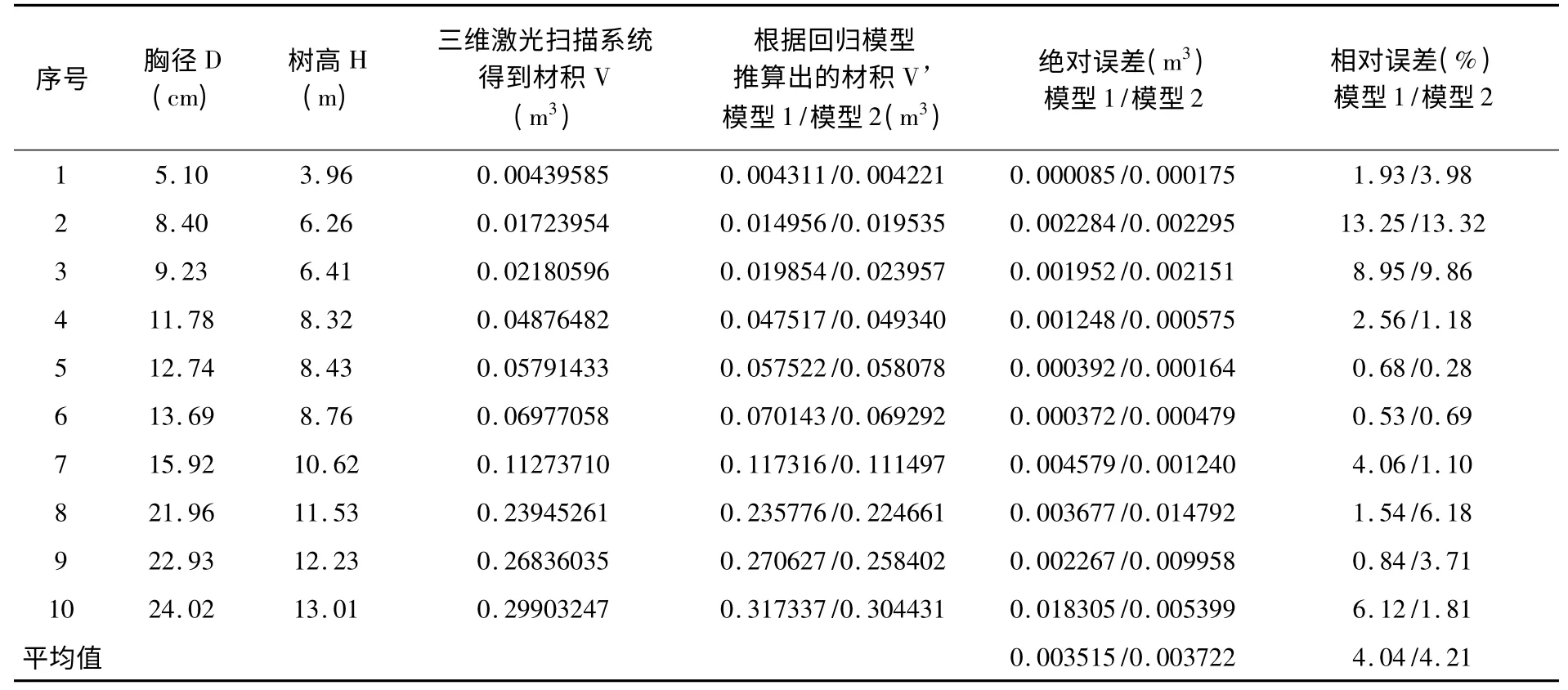
表6 银杏二元材积回归模型绝对误差和相对误差Table 6 The absolute error and relative error of binary volume model for Gingko

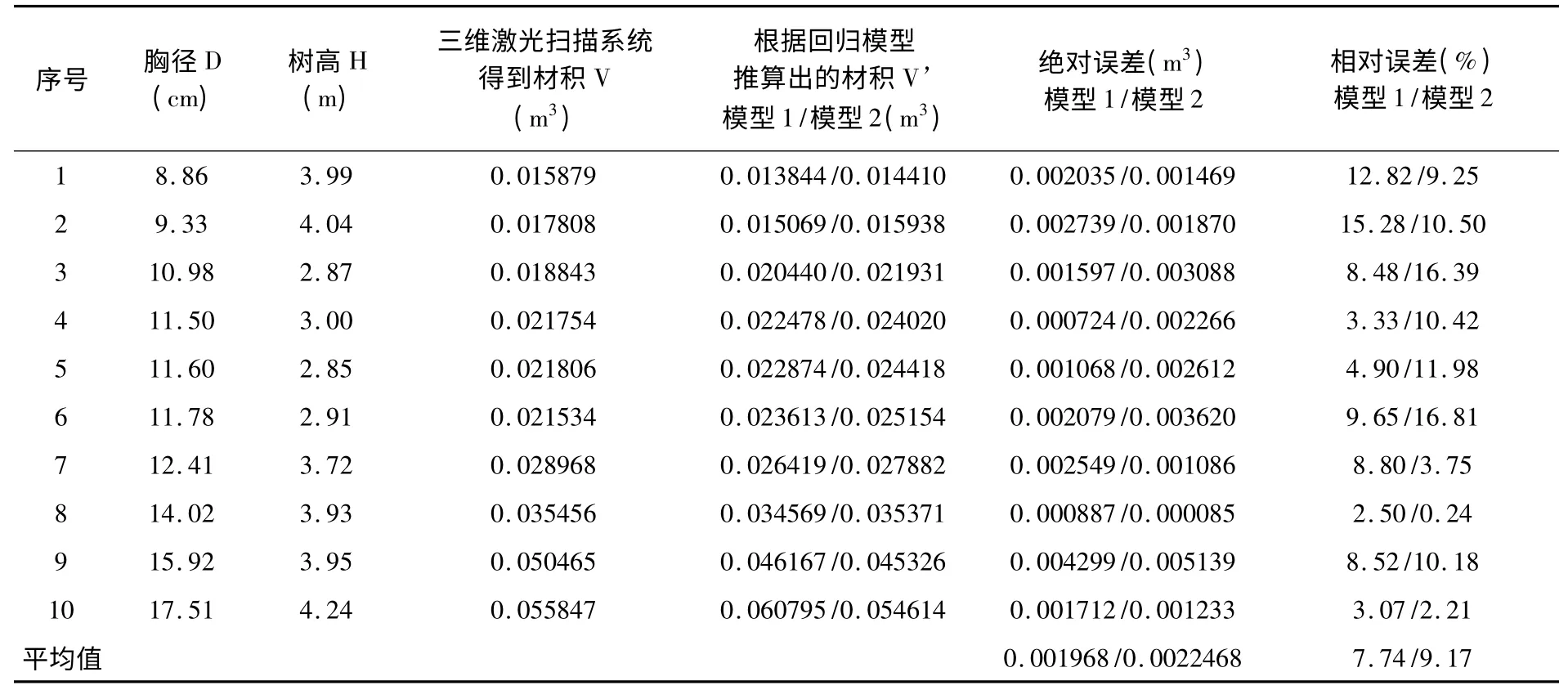
表7 龙爪槐一元材积回归模型绝对误差和相对误差Table 7 The absolute error and relative error of single tree volume model for Chinese pagoda tree

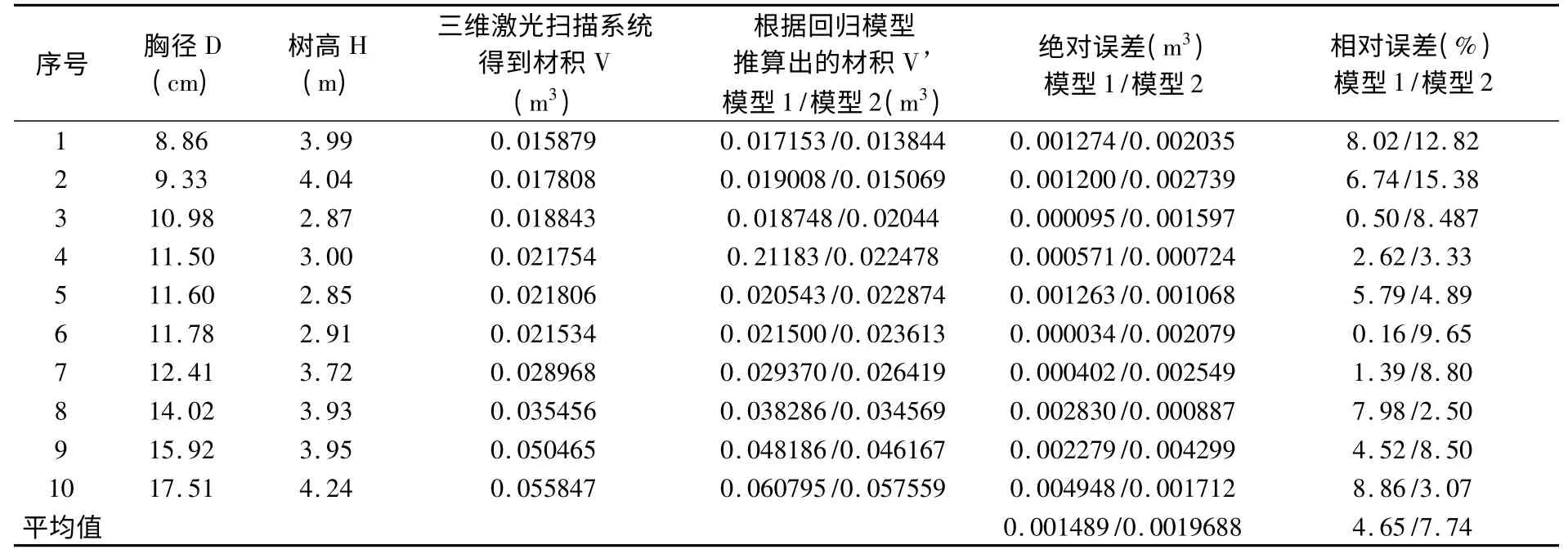
表8 龙爪槐二元材积回归模型绝对误差和相对误差Table 8 The absolute error and relative error of binary volume model for Chinese pagoda tree

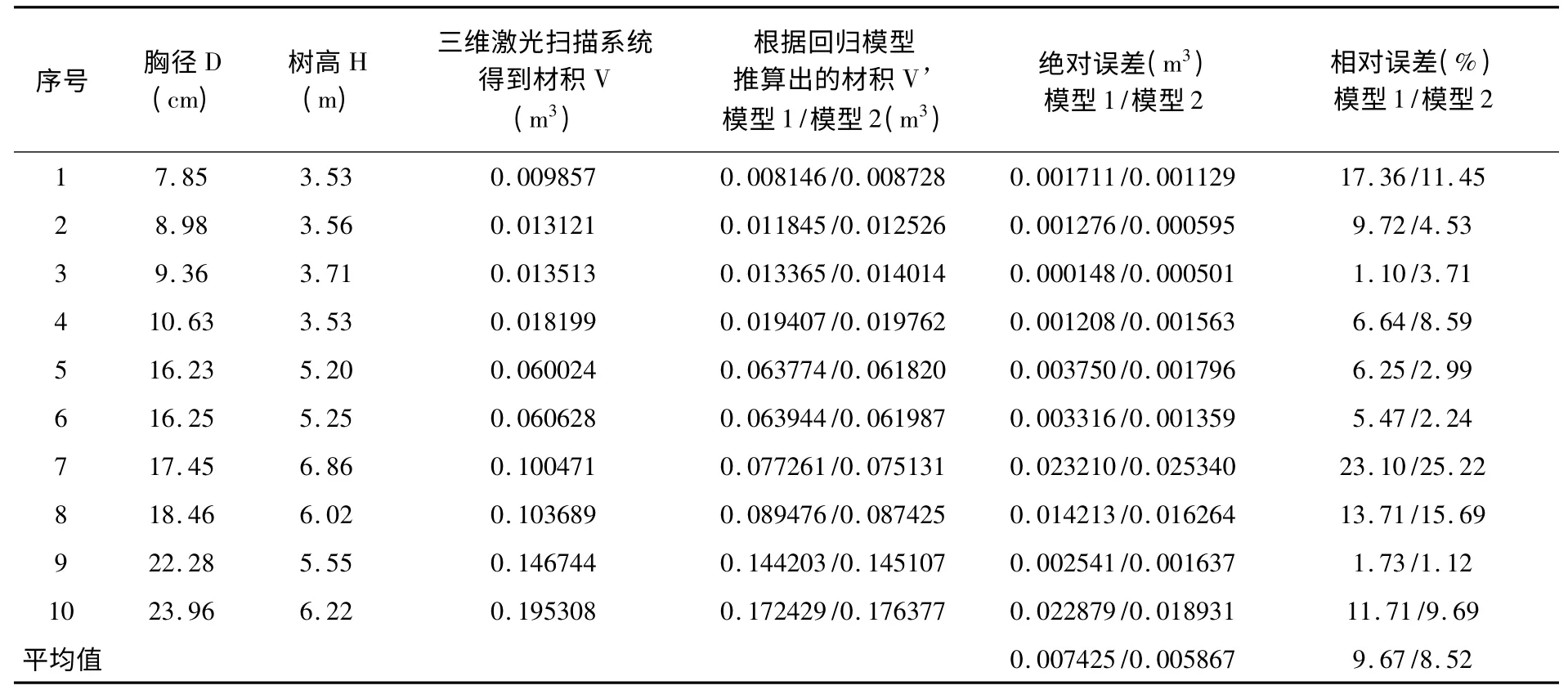
表9 油松一元材积回归模型绝对误差和相对误差Table 9 The absolute error and relative error of single tree volume model for Pinus tabulaeformis Carr

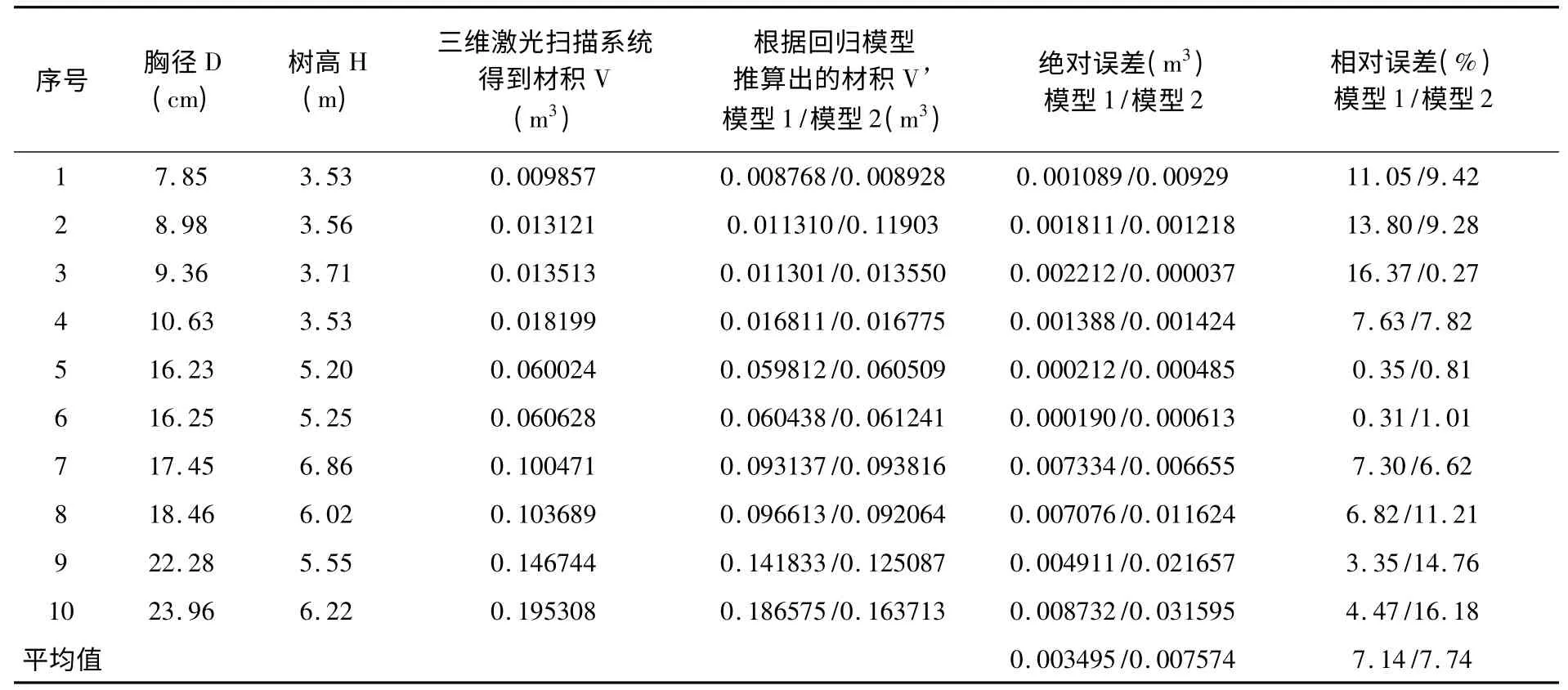
表10 油松二元材积回归模型绝对误差和相对误差Table 10 The absolute error and relative error of binary volume model for Pinus tabulaeformis Carr

从以上各表可以看出，用一元材积方程和二元材积方程分别去拟合样地的待测立木时，所得相关系数及系统误差值均明显可以看出二元的材积模型优于一元的材积模型的。计算所得的平均相对误差和绝对误差也是验证了此问题。即总体来说，明显二元的材积模型优于一元的材积模型，且在此样地内，关于银杏树种的二元材积模型最优，即:V=0.0318－0.4432d+1.3016d2+0.0946dh+0.1474d2h－0.0072h。

6 结语

综合以上各个回归模型的拟合结果分析和检验性分析，可以得出如下结论:①采用三维激光扫描系统获取的胸径、树高等测树因子，数据精确、不破坏立木的生长信息，并为建立回归模型提供精确的数据基础。②回归建立得到的一元立木材积模型、二元立木材积模型，通过实例验证表明最终所得模型所描绘的曲线与计算所得的材积曲线基本上是一致，说明这种方法能够用于推广回归建立立木材积模型及材积表，对于指导林业建立回归材积模型有普遍意义。③任何一个好的材积方程并不能对一切树种都能取得最佳效果，也不能对同一树种不同地区取得最佳效果。如何取得对不同树种及同一树种的不同生长环境立木材积，值得更进一步的探讨④本次研究是采用样地内的立木进行试验，范围小、数量少，如样本立木株树数量多时，能更高的提高精度，这部分工作有待探讨。

［1］吴春峰，陆怀民，郭秀荣，冯智超.利用三维激光扫描系统测量立木材积的方法［J］.森林工程，2009，05:71－72

［2］熊妮娜，王 佳，罗 旭，等.一种基于三维激光扫描系统测量树冠体积方法的研究——以油松为例［J］.北京林业大学学报，2007，29:61－65

［3］罗 旭，冯仲科，邓向瑞，等.三维激光扫描成像系统在森林计测中的应用［J］.北京林业大学学报，2007，29:82－87

［4］邓向瑞，冯仲科，马钦彦，等.三维激光扫描系统在立木材积测定中的应用［J］.北京林业大学学报，2007，29:74－77

［5］何 斌，冯促种，刘柯珍，等.云杉二元材积与蓄积量精度分析模型研究［J］.林业调查规划，2010，35(4):1－6

［6］王钦昊，卢丹阳.浅谈森林资源调查技术规定中立木材积表检验问题［J］.林业勘查设计，2009(1):33－34

［7］王仲锋，冯仲科.森林蓄积量与生物量转换的CVD 模型研究［J］.北华大学学报(自然科学版)，2006，07:265－268

［8］郭秀荣，陆怀民，杜丹丰.基于激光扫描的林木材积自动测量技术［J］.林业科学，2008，44:72－75

［9］张彦林，冯仲科，杨伯钢，等.LIDAR 技术在林业调查中的应用研究［J］.林业资源管理，2007，06，73－77

［10］吴明山.回归模型的估计方法及在林业中的应用研究［D］.昆明:西南林学院，2008

［11］王钦昊，卢丹阳.浅谈森林资源调查技术规定中立木材积表检验问题［J］.林业勘查设计，2009，01:75－79

［12］孟宪宇.测树学［M］.北京:中国林业出版社，1996

［13］Austin J M，Mackey B G，Van Niel K P.Estimating forest biomass using satellite radar:an exploratory study in a temperate Australian Eucalyptus forest［J］.Forest Ecology and Management，2003，176(3)，575 一583

［14］Jean－Francois Lalonde，Nicolas Vandapel and Martial Hebert.Automatic Three Dimensional Point Cloud Processing for Forest Inventory［D］.The Roboties Institute，Carnegie Mellon University，2006