风电引起3p闪变的仿真分析

胡 煜，伍青安，袁 越，吴博文，傅质馨

（1.河海大学 能源与电气学院，江苏 南京 210098；2.湖南省电力公司娄底电业局，湖南 娄底 417000）

0 引言

风电机组输出功率具有波动特性，大规模风电并网后会引起附近电网电压波动，当电压波动频率在0.05～35 Hz 范围内时，将引起人眼可察觉的闪变[1]。风电机组输出功率的波动主要是由风速的快速变动以及风剪、塔影效应等因素引起：较快的风速变动的变化频率约在0.1 Hz数量级，这种频率范围的电压波动引起闪变的可能性较小；由于自身结构的影响（如塔影效应等），风电机组在连续运行过程中会引起1 Hz数量级的电压波动，这种连续的电压波动可能会引起相对较严重的闪变问题[2]。文献[3]建立了风速和含风电机组的电网仿真模型，分析了风速变动和电网强弱对电压波动和闪变的影响，但忽略了风剪和塔影效应引起的3p（叶片旋转频率的3倍）脉动转矩对电压波动和闪变的影响。

国际电工标准IEC61400-21采用了一个无其他电压波动源的虚拟电网来模拟风电机组输出的电压，然后根据此模拟电压采用国际电工标准IEC 61000-4-15提供的闪变值仿真算法计算短时间闪变值。文献[4-6]基于IEC标准对风电引起闪变的测试与评估作了深入的研究。这种闪变值计算方法比较复杂，且在低频段检测误差较大。文献[7-8]根据IEC闪变仪的原理提出了基于谱估计的闪变计算，其基本思想是用快速傅里叶变换（FFT）分析出电压闪变调制信号的幅值和频率信息，乘以加权系数后取平方和得到瞬时闪变视感度，但FFT是假定分析时间段内信号是平稳的，不能反映非平稳信号的时变信息。

本文根据参考文献[9-10]建立了基于叶素理论的风剪和塔影效应模型，并将等效风速模型接入含风电机组的电网仿真模型中，在MATLAB／Simulink中仿真分析了风剪和塔影效应对电压闪变的影响。由于IEC闪变测试系统在低频段存在误差，针对风电引起的3p频率的低频闪变，将分析非平稳信号的希尔伯特-黄变换 HHT（Hilbert-Huang Transform）[11-12]用于分析风电引起闪变的时频特性，从时域和频域两方面同时对电压信号进行分析，提取非平稳电压闪变信号的时间、频率和幅值信息，计算闪变值。仿真验证了该方法在闪变检测中的正确性和有效性。

1 含风剪和塔影效应的等效风速模型

1.1 风剪效应模型

风剪效应是指风速随高度变化的特性对风机捕获功率的影响。风剪效应引起的转矩脉动是由风机每个桨叶旋转1周所经历的不同风况而产生的，目前常用的风剪模型为[9]：

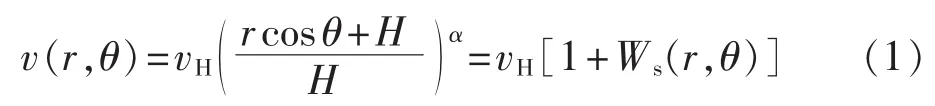
其中，r为桨叶叶素到转轴中点的径向距离；θ为方位角；vH为轮毂处的风速；Ws为风剪函数；α为风剪经验指数；H 为轮毂处高度；Ws（r，θ）为叠加在 vH上的风速扰动。

将 Ws（r，θ）进行 3 阶泰勒展开，并根据叶素理论得到三叶片风剪效应的等效风速：

其中，R为桨叶半径。

1.2 塔影效应模型

由塔架对风分布的影响所形成的对风机捕获功率的影响为塔影效应。风吹过塔架使塔架迎风面的风速减小，而当桨叶经过此区时，桨叶所产生的转矩将减小。目前常用的塔影效应模型为[9]：

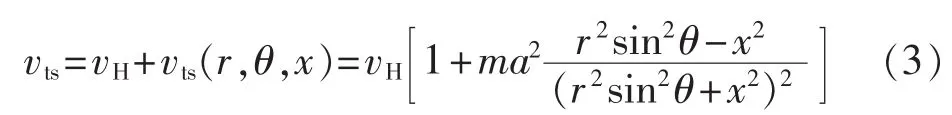
需要说明的是，塔影效应在90°≤θ≤270°时有效，其他时间水平轴风机桨叶转到上面平面，塔影效应消失。根据叶素理论得到三叶片塔影效应的等效风速：

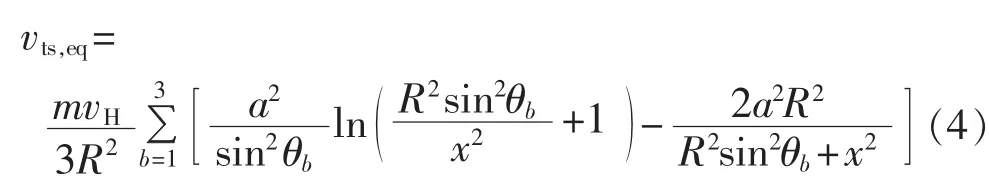
其中，θb为叶片方位角，三叶片依次相差120°。

1.3 含风剪和塔影效应的等效风速模型

含风剪和塔影效应的等效风速模型[9]如下：

仿真用风机参数：a=0.85 m；R=20 m；H=40 m；x=2.9m；vH=10m／s；α=0.3；风轮额定转速取 20r／min。

由图1，塔影效应（标幺值）引起的脉动远远大于风剪效应（标幺值），风剪和塔影效应引起的脉动频率为风机旋转频率的3倍，与已有结论一致。

图1 仿真得到的风剪和塔影效应对等效风速的影响Fig.1 Impact of wind shear effect and tower shadow effect on equivalent wind speed by simulation

2 基于HHT的闪变检测

2.1 HHT的基本原理

HHT由经验模态分解EMD（Empirical Mode Decomposition）和Hilbert变换两部分组成。先从信号本身的尺度特征出发，采用EMD提取信号的固有模态函数 IMF（Intrinsic Mode Function），然后对 IMF分量作Hilbert变换求出瞬时频率和瞬时幅值[11-12]。对于分解总阶数为n的时间序列，可以表示为：

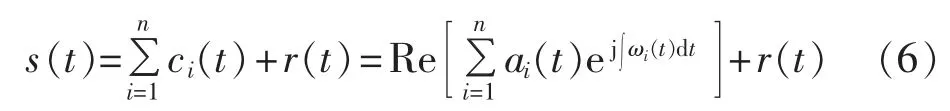
其中，c（t）为 IMF 分量；r（t）为残余函数，它是一单调函数，为数据的均值或趋势；a（t）、ω（t）分别为各个IMF分量的幅值和角频率，是时间的函数。它可看作一般化的傅里叶展开，突破了传统傅里叶常数幅度和一定频率的限制，使得这种方法能有效地处理非平稳信号。

2.2 基于谱估计的闪变值计算

根据文献[7]，瞬时闪变值 s（t）可按式（7）计算，当电压波动波形和频率固定时，短时间闪变值Pst可按式（8）计算：

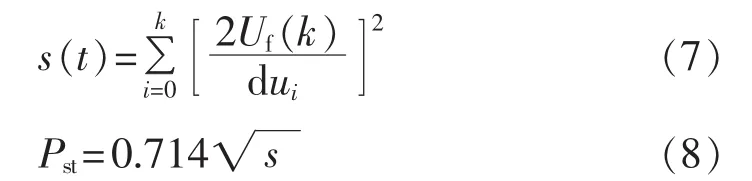
其中，Uf（k）为闪变调制信号幅值；k为调制分量个数；dui为单位瞬时闪变值对应的正弦波电压波动值。

2.3 算例验证

具有波动和闪变特征的电网电压可视为工频正弦电压的一种调幅波，其电压有效值或峰值的包络线可以反映闪变的特征。对于任何波形的调幅波均可看作是各种频率分量的合成，如下式所示：

其中，A0为供电电压的标称幅值；f0、φ0为基波频率和相角；Ai、φi为调幅波分量的幅值和相角。闪变低频调制信号频率范围为0.05～35 Hz，是人眼视觉的敏感区域。设采样频率3200 Hz，电压闪变信号为：

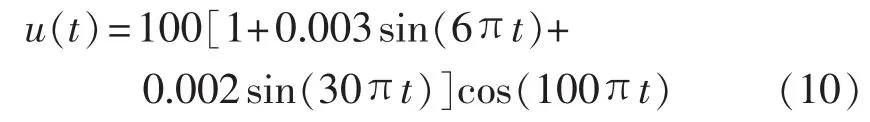
HHT时频分析的结果如表1所示。可见，估计值与设置值的偏差均较小，HHT能准确地检测多频率调制闪变信号的频率和幅值信息。

表1 闪变仿真参数的设置值和估计值Tab.1 Set simulative parameters and estimated results of voltage flicker

对单位瞬时闪变值对应正的弦波电压波动值表[9]作插值，可得到频率为 0.2992 Hz、15.027 Hz 时分别对应的正弦波波动值为0.654%和0.432%，代入式（7）和式（8）可得瞬时闪变值为 1.692，短时间闪变值为0.9287。根据IEC闪变测试系统模型在MATLAB／Simulink 搭建闪变仪[6]，测量结果为瞬时闪变值1.6648，短时间闪变值0.9213。测量结果十分接近，验证了基于HHT闪变检测的有效性。由于IEC闪变仪在小于3 Hz的低频段闪变检测时误差较大，而风电引起的电压闪变主要位于该频率段[7]，因而下文采用基于HHT的闪变检测来分析风电引起的电压波动和闪变。

3 风电引起3p闪变的仿真分析

依据风剪效应和塔影效应的等效风速模型，建立含风电电网的仿真模型。风电场由定速异步风电机组成，总容量9 MW。通过长度为50 km的输电线路并入电网。MATLAB／Simulink中搭建的含风电电网的仿真模型如图2所示。

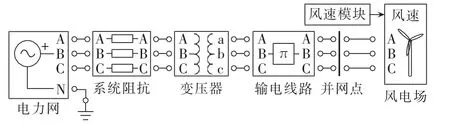
图2 含风电电网的Simulink仿真模块Fig.2 Simulink simulation module of grid with wind farm

将第1节等效风速模型接入含风电电网的仿真模型中，得到并网点的电压波形如图3（a）所示，采用HHT对其进行时频分析。由图3（b）可知：闪变信号第1个分量IMF1为主要分量，其幅值为0.0059 p.u.，中心频率为0.9902 Hz，十分接近3p频率，由于本文采用的是定速风电机组，因而闪变频率基本不变；闪变信号第2个分量IMF2幅值很小，可忽略；电压均值（基波有效值）约为0.9744 p.u.。因而，塔影效应引起的闪变强弱取决于主调幅波幅值的大小。该算例中，主振动模态的幅值占基波幅值的百分比为0.61%，对应瞬时闪变值为0.7047，短时间闪变值为0.5994。

图3 风电引起电压闪变信号的HHT分析Fig.3 HHT analysis of voltage flicker caused by wind farm integration

FFT分析结果为：直流分量幅值0.974p.u.；1Hz分量幅值 0.005892 p.u.；2 Hz 分量幅值 0.000617 p.u.；3 Hz分量幅值0.000 169 p.u.。对应瞬时闪变值为0.735 8，短时间闪变值为0.6125，检测结果十分接近，进一步验证了HHT在风电引起的3p闪变检测上的有效性。

下面分别对桨叶旋转平面到塔架中线的距离、塔架半径、桨叶半径和轮毂高度对闪变的影响进行分析。

电压闪变主调幅波的相对幅值随桨叶到塔架中线距离x的变化如表2所示，闪变值随桨叶到塔架中线距离的增大而减小。

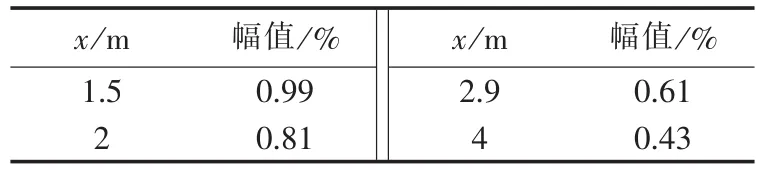
表2 不同桨叶到塔架距离下的闪变值比较Tab.2 Magnitude of voltage flicker for different distances between tower and blades

假定桨叶旋转平面到塔架表面的距离不变，即x=2.9-0.85+a，电压闪变主调幅波的相对幅值随塔架半径的变化如表3所示，闪变值随塔架半径的增大而增大。

表3 不同塔架半径下的闪变值比较Tab.3 Magnitude of voltage flicker for different tower radiuses

电压闪变主调幅波的相对幅值随桨叶半径的变化如表4所示，闪变值随桨叶半径的增大而减小。

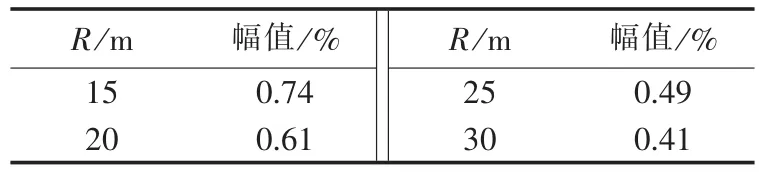
表4 不同桨叶半径下的闪变值比较Tab.4 Magnitude of voltage flicker for different blade radiuses

电压闪变主调幅波的相对幅值随轮毂高度的变化如表5所示，闪变值基本不随轮毂高度变化。

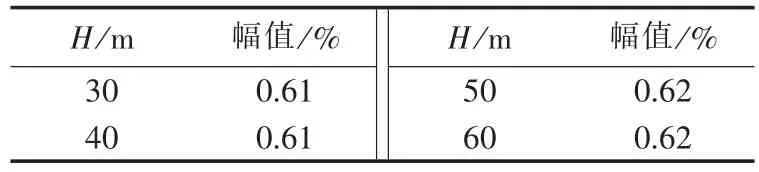
表5 不同轮毂高度下的闪变值比较Tab.5 Magnitude of voltage flicker for different hub heights

4 结论

本文根据叶素理论建立了风剪效应和塔影效应的等效风速模型，在MATLAB／Simulink中搭建含风电电网的仿真模型，仿真分析了风剪效应和塔影效应引起的3p频率的电压闪变。采用Hilbert-Huang变换对其进行分析，得出如下结论：风电机组塔影效应引起的电压波动和闪变的频率为风轮转速的3倍，闪变值随桨叶半径和桨叶旋转平面到塔架距离的增大而减小，随塔架半径的增大而增大，轮毂高度和风剪效应对闪变的影响很小。