采用多目标网格进化算法并面向对象的舰船电网重构

蒋燕君，姜建国，张宇华

（1.上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240；2.浙江树人大学 信息科技学院，浙江 杭州 310015）

0 引言

由于舰载高能武器发射、大功率探测和快速推进等供电需要，舰船电力系统呈现出高度集成化趋势，且供电连续性和可靠性要求更苛刻，使舰船电网规模与复杂性大为增加。为保障舰船多样化电力需求，舰船电网智能重构NR（Network Reconfiguration）十分必要。

舰船电网重构是一个多目标多约束的优化决策问题[1-10]。通常重构目标与约束条件保持不变，重构目标间偏好关系由实时电力调度决定而经常发生变化，因此为提高获取全局最优解的效率，以获得一组Pareto最优解集为目标的本质多目标方法逐渐替代以获得一个全局最优解为目标的传统多目标方法。但当重构目标个数超过3时，多数Pareto方法[11-14]在判别解的非支配关系上需耗费大量时间，难以满足舰船电网重构快速性需求。面向过程的Pareto重构策略不但可扩展性较差，且相互间难以客观公正地进行性能比较。同时由于重构问题的真正Pareto前沿往往未知，这给算法性能指标的计算带来很大困难。

针对以上不足，本文提出基于多目标网格进化并面向对象的舰船电网智能重构策略，该方法采用局部搜索技术，能有效缩短搜索时间，且基于Java的面向对象设计使算法具有良好的移植性和可扩展性，同时其公共平台的建立让不同Pareto方法间性能比较成为可能。最后对舰船电网的3个算例进行重构测试。

1 舰船电网重构模型

1.1 目标函数

舰船电网重构建模主要考虑以下几个目标：系统失电负荷量尽可能小；电网有功损耗尽可能小；线路负荷分配失衡度尽可能小；开关操作次数尽可能少。因此舰船电网重构目标描述如下：

其中，f1（X）为系统失电负荷量，Li为母线i处负荷，B1为重构前电网供电母线集，B2为重构后电网供电母线集；f2（X）为重构后电网有功损耗，可由潮流计算求得，Ri为线路i的电阻，Ui、Pi和 Qi分别为线路 i末端母线的电压、有功和无功，E为电网中线路总数；f3（X）为重构后线路负荷分配失衡度；f4（X）为参与重构的开关操作次数，xi1、xi2分别为重构前、后开关i的状态，N为开关总数；X为开关序列状态向量，也即决策变量，xi为开关 i的状态，xi（i=1，2，…，N）取值1或0分别表示开关i处于闭合或断开状态。

重构操作将使电网拓扑发生改变，引起电网供电母线集B2产生变动，导致线路负荷分配情况发生变化，因而负荷分配失衡度f3（X）能客观地反映出重构后负荷分配实际均衡状况。

1.2 约束条件

a.重构后舰船电网仍需保持辐射状结构。

b.母线电压需维持在允许范围内：

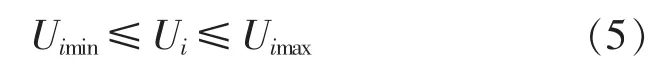
其中，Ui为母线i的电压，Uimin和Uimax分别为母线i运行时电压的最小和最大允许值。

c.线路电流需维持在允许范围内：

其中，Ii为线路i的电流，Iimax为线路i运行时电流的最大允许值。

1.3 偏好知识

本文假设重构时根据实际需要确定4个目标函数间的偏好关系有以下2种可能。

a.舰船电网正常运行时的重构：

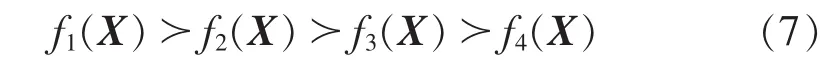
b.舰船电网故障恢复时的重构：

其中，“≻”表示“偏好大于”。

2 多目标网格进化算法

多目标网格进化算法 MGEA（Multiobjective Grid Evolutionary Algorithm）保留了问题的多目标本质，采用外部存档策略来存储非支配解[11-12]，利用反馈机理将从档案中选取的非支配解随机地替代子代种群中的部分个体，是一种获取Pareto前沿的精英算法[15-17]。 MGEA 如表 1 所示。

表1 多目标网格进化算法Tab.1 Multiobjective grid evolutionary algorithm

算法第2行中，对算法需要的变量、参数和算子进行初始化。第3行先产生初始种群，再建立二维环形网格，并将初始种群中所有个体逐个放置在网格中。第4行建立一个空的Pareto前沿。对于种群pop的每个个体，根据个体所在位置可知其邻域范围，从而获取相应邻居neighbors（第7行）。从neighbors中选取2个个体作为双亲parents，以概率Pc进行交叉，得到子代offspring，再以概率Pm对offspring进行变异，并对经选择、交叉和变异得到的个体进行评价（第8—11行）。第12行中辅助种群aux_pop初值为第3行产生的初始种群；若按定义1判断，个体offspring优于individual，则aux_pop位于原网格上的individual被offspring替换。这里定义1中的指定种群是由 neighbors、individual和 offspring共同组成的。如果个体 offspring不被individual支配，则把offspring增加到Pareto_front中，若此时Pareto_front个数刚越界，那么舍去在Pareto_front中具有最小拥挤距离[12]的个体（第13行）。待种群 pop中所有个体都完成第7—13行操作后，从Pareto_front中选取一定量个体随机地替换aux_pop中相同数量的个体（第15行），再把旧种群pop替换成辅助种群aux_pop（第16行）。上述迭代过程一直进行到满足终止条件termination_condition为止。MGEA中一代种群的进化过程如图1所示。

定义1 设解X优于解Y，则下列条件之一成立：解X支配解Y；解X与解Y互不支配，且在指定种群中解X比解Y具有更大的拥挤距离。

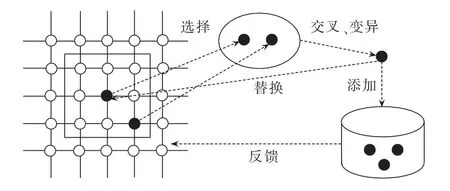
图1 一代种群的进化过程Fig.1 Evolutionary process of one generation population

MGEA中，个体的邻域（Neighborhood）是指该个体邻近网格位置的集合。不同形状的邻域对MGEA的性能有较大的影响。按模式不同，邻域可分为线性和紧凑2种。常见的邻域形状有L5（Linear 5）和C9（Compact 9）2 种，如图 2 所示。

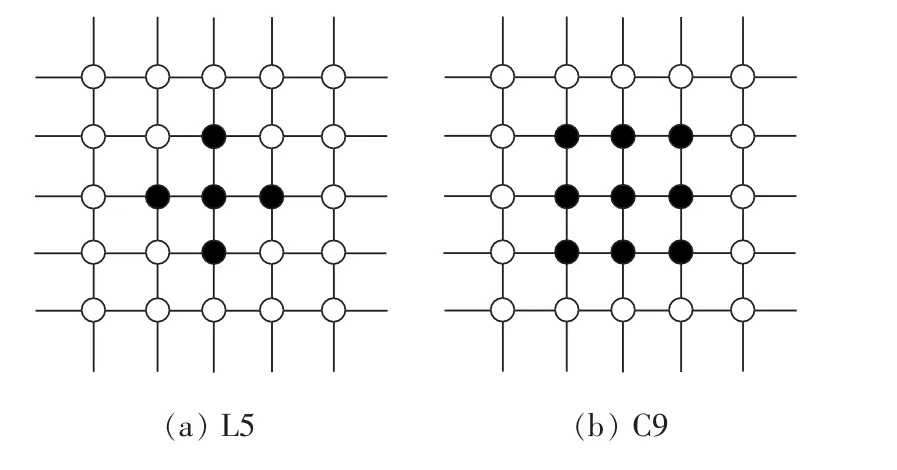
图2 邻域形状Fig.2 Neighborhood shape

从表1可知，选择、交叉和变异算子仅作用在个体邻域范围内，减缓了基因扩散速度，因而MGEA本质上是一种局部搜索算法。需要说明的是，种群pop需完成一次迭代后，才借助辅助种群aux_pop实现一次性更新，即同步更新。根据实际需要，也可采用异步更新。

3 面向对象的舰船电网重构框架

采用面向对象技术实现舰船电网重构，主要基于以下考虑：将各种重构算法的公共属性和操作抽象出来形成共同的基础类平台，使不同算法能在同一平台上客观公正地进行性能比较；为算法选择适合实际重构问题的参数和算子提供便利和灵活性；基于Java语言的面向对象设计具有良好的可移植性和可扩展性。

图3为舰船电网重构基础类图。图中，“*”指0个或多个，“1..*”指1个或多个，电网重构基本框架由算法（Algorithm）、算子（Operator）、问题（Problem）、解的类型（SolutionType）、变量（Variable）、解（Solution）、解集（SolutionSet）共 7个类组成。 每个类均由类名、属性（域）和操作（方法）3 个部分构成[18]。

所有启发式算法（如 MGEA、NSGA-Ⅱ[12]、SPEA2[14]等）均为抽象类Algorithm的子类，该基类中的抽象方法execute（）须在子类中实现，其功能是启动算法执行，并返回一个种群。基类Operator主要有选择、交叉和变异等子类。启发式算法正是通过应用不同算子实现旧解生成新解。所有问题均继承于基类Problem，其核心方法evaluate（）实现对解的评价。据问题实际，即可确定解的类型。基类SolutionType的子类有 BinarySolutionType、RealSolutionType 等，其抽象方法createVariables（）建立构成解的变量数组。基类Variable有Binary、Real等子类，这些不同子类实例可联合构成同一个解。从进化角度来看，SolutionSet、Solution、决策变量（Variable[]）以及变量（Variable）分别等价于种群、个体、染色体和基因。

4 基于MGEA的舰船电网重构实现

4.1 重构问题子类设计

重构问题是基类Problem的子类。子类NR由域、构造器 NR（String solutionType）和方法 evaluate（Solution solution）组成。域包括重构前网络结构（含线路号及对应母线号）、线路参数、负荷数据和电源电压等。类NR核心方法evaluate（）实现对解的评价，其过程如表2所示。

表2 解的评价过程Tab.2 Procedure of solution evaluation

算法第2行中，对计算目标值和约束违背值所需的所有原始数据进行初始化。从方法参数solution中提取决策变量值variables（第3行）。结合实际，按以下3点对variables进行检测：若有故障，则故障区域是否被隔离；电源是否连通；电网是否呈辐射状。如有必要，则进行修正（第4行）。将修正后的决策变量保存到方法参数solution中（第5行）。对照原始电网结构，获得与修正后的决策变量相对应的电网拓扑，按潮流计算要求对其进行拓扑识别（第6行）。结合原始数据进行潮流计算（第7行）。根据潮流计算结果和式（1）—（6），进一步计算目标值和约束违背值，并把最终结果保存到方法参数solution中（第8—10行）。

图3 舰船电网重构基础类图Fig.3 Base class diagram of shipboard power network reconfiguration

4.2 重构项目主类设计

重构项目主类名为MgeaNR，由2个域logger、fileHandler和 1 个 main（String[]args）方法组成。 设置这2个域的作用是以文件形式将重构程序运行过程中产生的重要信息记录在日志中。类MgeaNR方法main（）实现对舰船电网的重构，其过程见表3。

表3 舰船电网重构过程Tab.3 Procedure of shipboard power network reconfiguration

算法第2行中，给定问题、算法和算子，将算法参数和算子初始化，再把算子添加到算法中。执行算法，并返回一个种群（第3行）。将算法执行时间记录在日志中（第4行）。把目标值和对应的决策变量值保存到指定路径的文件中（第5行），同时路径和文件名记录在日志中（第6行）。从返回的种群中获取Pareto前沿front（第7行）。由 front计算出超体积（第8行），并记录在日志中（第9行）。

可借助NetBeans或Eclipse开发环境运行主类MgeaNR，实现基于MGEA的舰船电网重构。

5 重构算法的性能指标

为定量分析多目标重构算法性能，选择能同时兼顾收敛性和多样性的超体积作为评价指标。文献[17，19-21]根据算法获得的非支配解来选择超体积计算所需的参考点，这给不同算法间的性能比较造成很大困难。为此，本文始终以目标空间原点作为参考点，来计算Pareto前沿的超体积。以二维目标空间为例，超体积计算示意图如图4所示。

图4 二维目标空间中的超体积计算Fig.4 Hypervolume calculation in 2-dimensional objective space

假设Pareto前沿由3个非支配解a、b、c组成，则分别从点a、b、c向2个目标轴作垂线围成多边梯形a2aa1bb1cc1oa2，该多边梯形面积即为此Pareto前沿对应的超体积HV。通过虚线b2a1、c2b1将多边梯形分割成 3 个小矩形 a2aa1b2、b2bb1c2、c2cc1o，依次记这些小矩形面积为 V1、V2、V3，则：

同理，三维目标空间中的超体积计算示意图如图 5所示，图中的 V1、V2、V3分别表示最下面、中间、最上面的多面立方体的体积，由非支配解a、b、c构成的Pareto前沿的超体积计算公式同式（9）。不难发现，从下到上的3个多面立方体底面积正是3组非支配解（abc）、（ab）、a 分别在 f1f2平面上的投影构成的Pareto前沿在二维目标空间中的超体积。依此类推，通过递归调用，可计算出四维及以上目标空间中的超体积。

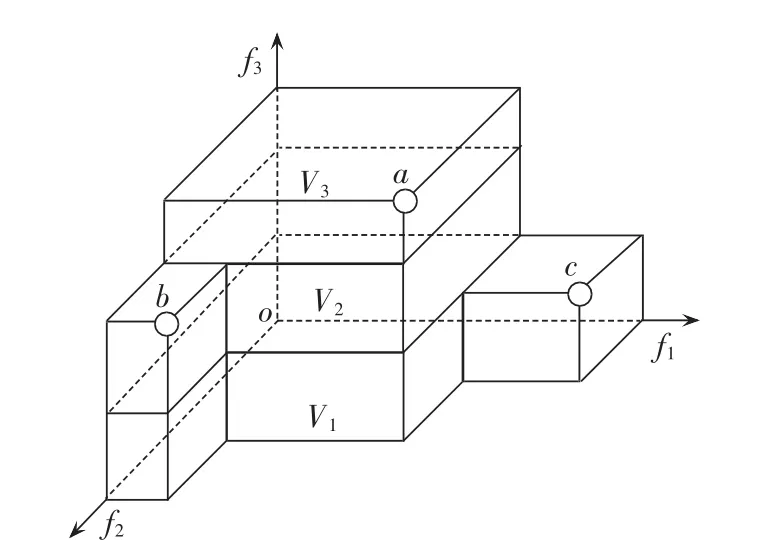
图5 三维目标空间中的超体积计算Fig.5 Hypervolume calculation in 3-dimensional objective space

由于上述超体积的计算视原点为参考点，且重构为目标最小化问题，故算法获得的Pareto前沿越接近真正Pareto前沿，其超体积越小。同时Pareto前沿中解的多样性越佳，其超体积也越小。实际问题中，因真正Pareto前沿未知，造成无法获知求得的Pareto前沿与真正Pareto前沿间的接近程度，故只能通过比较超体积大小来判断重构算法性能优劣。

6 算例分析

本文在NetBeans 7.0和Java jdk1.6.0_26平台上实现电网重构，并用3个算例进行验证。测试所用电脑配置为：AMD Athlon64 X2 4 000+，主频2.11 GHz，1 GB内存。以文献[22]附录A舰船电网结构、线路和负荷数据为例，电源电压U1=11 kV。3种算法的算子和参数设置如表4所示。假定由于某种原因（如线路维护或故障等）要求在电网重构过程中始终保持断开的线路如表5所示。

表4 3种算法的算子和参数设置Tab.4 Operator and parameter settings of three algorithms

表5 算例1—3的断开线路Tab.5 Disconnected lines in case 1-3

NSGA-Ⅱ[12]是由 Deb K 在 2002 年提出的一种基于非支配排序和精英策略的快速多目标进化算法。 SPEA2[14]是由 Zitzler E在 2001年提出的一种基于细颗粒适应度分配、密度估计和外部存档策略的多目标进化算法。NSGA-Ⅱ和SPEA2是在多目标进化界最具代表性的2种算法。

为反映统计数据中各变量的集中趋势和分散情形，并避免极端变量值影响，本文采用中位数和四分位距进行统计分析。表6和表7分别为3种算法独立运行30次得到的运行时间和超体积指标的统计分析，其中Mv是中位数，Iqr是四分位距。由表6可知，MGEA所需运行时间最少，运行速度的稳定性最好；NSGA-Ⅱ所需运行时间比MGEA略长，运行速度的稳定性最差；SPEA2所需运行时间最长，是NSGA-Ⅱ的3.5～5.6倍，是MGEA的5.5～9.3倍，运行速度的稳定性尚可。由表7可知，MGEA在算例1、3中超体积指标优于其他2种算法，但指标大小的稳定性最差；NSGA-Ⅱ在算例2中超体积指标优于其他2种算法，其指标大小的稳定性稍差；SPEA2在算例2中超体积指标优于MGEA，劣于NSGA-Ⅱ，其指标大小稳定性极好。综上所述，MGEA在舰船电网重构中的表现优于NSGA-Ⅱ和SPEA2。

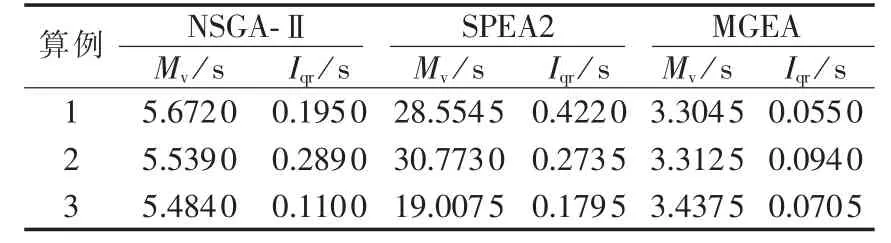
表6 3种算法运行时间的统计分析Tab.6 Statistical analysis of calculation time for three methods

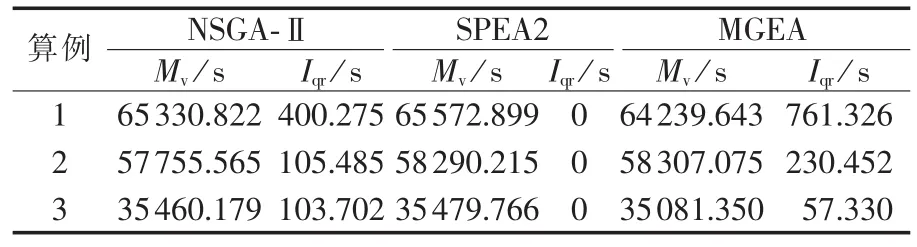
表7 3种算法超体积指标的统计分析Tab.7 Statistical analysis of hypervolume metric for three methods

表8为上述3种算法在不同偏好关系下获得的计算结果，其中 P1和 P2分别表示式（7）和（8）中所描述的目标偏好关系。此结果是在运行算法所获得的Pareto最优解集中选取与不同偏好关系相应的最优解而得到。由于3种算法所获得的计算结果一致，因而表明这些算法均具有获取全局最优解的能力。从表8可知，同一算例在不同偏好关系下所获得的最优解可能不同（如算例1和2），也可能相同（如算例3）。除可行解集的限制外，这主要依赖于算法所获得的Pareto最优解集的多样性。

表8 不同偏好关系下算例1—3的计算结果Tab.8 Computational results of case 1-3 under different preference relations

7 结论

本文提出的基于MGEA并面向对象的舰船电网智能重构策略，与NSGA-Ⅱ和SPEA2相比，在算法运行速度方面具有明显的优势，在算法收敛性能与解的多样性分布方面具有一定的优势，而面向对象的设计不但使其具有良好的移植性和可扩展性，而且实现了基于同平台的不同算法性能的客观比较。对供电连续性要求苛刻的舰船电网而言，重构快速性甚至比全局最优性更为重要，而对于二者均能兼顾地采用MGEA的重构决策方法，无疑具有广阔的应用前景。在评价重构算法性能时，本文没有考察不同参数设置对算法产生的影响，因而在基于MGEA重构技术的后续研究中，可着重考察算法对网格大小、邻域形状、反馈个数和档案大小等参数不同设置时的灵敏度，以便进一步完善。