Zn 空位及Cu 掺杂对ZnTe 电子结构及光学性质的影响

李清芳，胡 舸*，姚 靖，张 双，魏 胜，封文江

(1.重庆大学化学化工学院 化学系，重庆 400044;2.沈阳师范大学 物理科学与技术学院，辽宁 沈阳 110034)

1 引 言

ZnTe 为立方闪锌矿结构的Ⅱ-Ⅵ族化合物半导体材料，禁带宽度为2.26 eV，可重掺杂［1］。ZnTe 在光敏陶瓷、压电器件及太阳能电池材料等诸多领域具有广阔的应用前景，受到了国内外各研究领域的重视［2-3］。近10年来，人们一直致力于研究ZnTe 的电子结构和光学性质，以设计新型半导体材料。K.B.Joshi 等［4］采用经验赝势方法与康普顿计算方法研究了ZnTe 的电子能带结构、电子动量密度分布及其能带分解自相关函数。X.H.Zhou 等［5］采用从头计算法研究了3d 过渡金属Cr、Mn 掺杂的ZnTe 薄膜的电子结构和磁学性质。N.G.Szwacki 等［6］采用从头计算方法研究了MnTe、ZnTe 和ZnMnTe 的结构特性，结果表明，闪锌矿比纤锌矿稳定。Y.Uspenskiia 等［7］采用TB-LMTO 方法计算研究了掺V、Cr、Mn、Fe 和Co 的ZnTe 的电子结构和磁学性质，其结构表明掺杂过渡金属对ZnTe 的铁磁和反铁磁稳定性造成了很大影响。C.Tablero 等［8］计算研究了O 掺杂ZnTe 的总电子能，进而获取了其电子电离能。尽管人们对ZnTe 结构本体及ZnTe 掺杂体系的电子结构和光学性质的研究已取得了一定的成果，然而却很少有人研究ZnTe 空位缺陷以及Cu 掺杂超晶胞的微观结构及性能。本文中采用基于密度泛函理论的第一性原理平面波赝势方法，对ZnTe 结构本体、Zn 空位及Cu 掺杂3 种超晶胞进行结构优化处理，计算并详细分析了几种体系下ZnTe 材料的缺陷形成能、态密度、能带结构、集居数、介电函数、损失函数、吸收光谱、光电导率、复折射率及反射率，以期揭示Zn 空位及掺Cu 对ZnTe 电子结构和光学性质的影响。

2 计算方法和模型

2.1 计算方法

本文采用基于密度泛函理论的平面波赝势法(PWP)和广义梯度近似(GGA)对体系中的交换相关能进行计算处理，其中相关的算法已植入Perdew-Burke-Ernzerh 机理于CASTEP 中［9］。由于Zn3d104s2、Te5s25p4和Cu3d104s1的能量相对较高，同时内层电子对材料的性质影响不大而外层电子又比较活泼，因此在计算中将其作为价电子层，视作价态处理。k 网格(k-mesh)大小为4 ×4 ×4，平面波截止能量、原子间相互作用力收敛标准与能量收敛标准分别设为400 eV、0.1 eV·nm-1、1.0 ×10-5eV·atom-1，总应力张量减小到约0.02 GPa。

对于缺陷体系，本文按照如下方程来计算的缺陷形成能(用Ef表示)［10-11］:

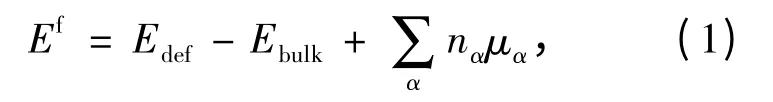
其中，Edef、Ebulk分别是缺陷超晶胞和理想超晶胞的能量，nα代表体系产生空缺缺陷需要移出或掺杂进的α 原子的个数，相应的化学势用μα表示。

Zn 和Te 的化学势的确定需取决于晶体生长条件，不能由总能量唯一确定，还需设定一定的边界条件，因此本文采用μZn+μTe=EZnTe来表示能量条件，其中EZnTe表示晶胞中一对原子的总能量。为了防止纯Zn 的形成，则应有μZn≤μZn(bulk)，其中μZn(bulk)表示单个六边形封闭结构的锌原子的总能量。根据上述限定条件不难看出，富锌条件下的ZnO 中的Zn 原子的化学势就满足关系μZn=μZn(bulk)，另一方面，也有μTe≤μTe(bulk)，否则单个Te 原子就要比ZnTe 晶胞中Te 原子更为稳定了，同时还可能形成Te 单相。考虑到ZnTe 的热稳定性条件，单晶的形成焓ΔH(ZnTe)可由变量μZn和μTe表示［12］为:

则在富锌条件下，有μZn=EZn，μTe=ΔH(ZnTe)-EZn;同样，对于复碲体系，μTe=ETe，μZn=ΔH(ZnTe)-ETe。

光学性质的计算需要密集均匀分布的k 点网格，本文采用一个由20 ×20 ×20 的Monkhorst-Pack 点集成的布里渊区进行计算。采用介电函数来计算体系的光学性质，考虑到吸收的影响，介电函数用复数ε(ω)=ε1(ω)+iε2(ω)来描述，因此，应用Kramers-Krõnig 关系，可推导出虚部ε2和实部ε1的表达式［13-14］如下:

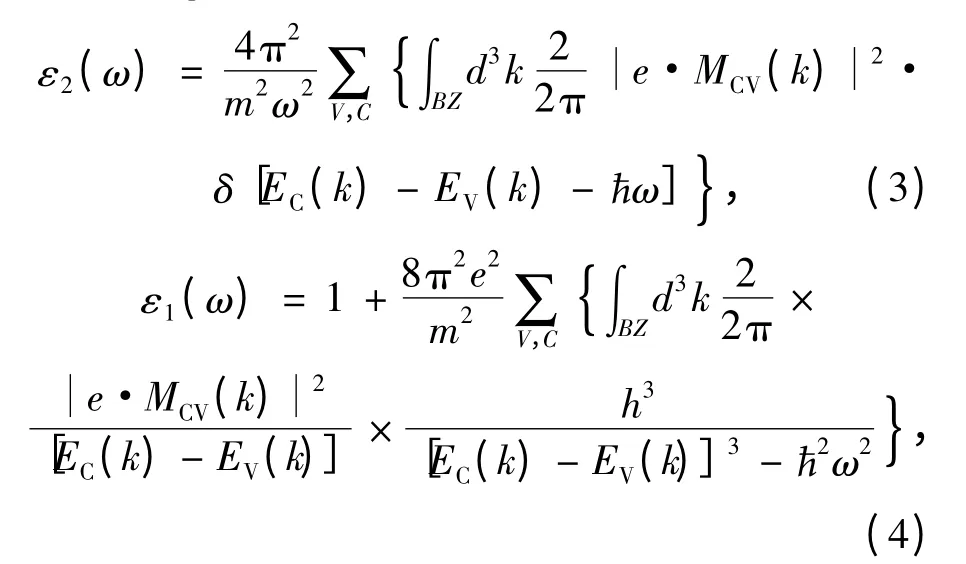
电子能量损失函数与介电常数直接相关，其表达式［14］为:

吸收光谱则采用如下方程［15〛进行计算:

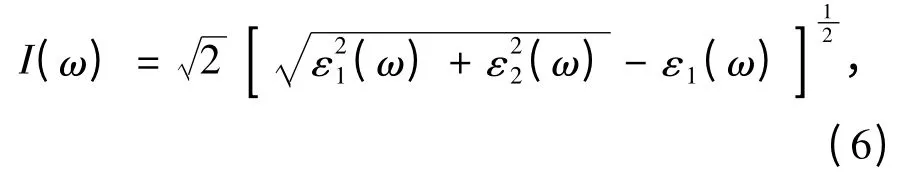
此外，介电函数的实部ε1和虚部ε2还满足如下关系式［14］:

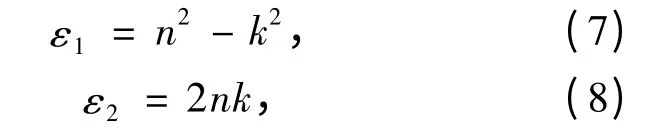
即为复折射率和介电函数的关系式，可见用n、k也能描述体系的光学性质。采用该关系式还可得到3 种晶系的复折射率。

光直接垂直入射到具有复折射率的介质中时，n1=1，n2=n+ik，可得到反射系数的表达式［14］为:

2.2 计算模型

图1 2 ×1 ×1 缺陷ZnTe 超晶胞结构。X:Zn 空位或掺杂原子Cu。Fig.1 Supercell (2 ×1 ×1)of ZnTe with defect.X:Zn vacancy or impurity Cu.

3 结果与讨论

3.1 结构性能

对3 种体系超晶胞进行结构优化，可得到体系的稳定结构。表1 总结了3 种体系的晶胞参数。可以看出，Zn0.875Te 的体积略小于ZnTe 的，这是Zn 空位缺陷引起的;而Zn0.875Cu0.125Te 的体积减小则是由于Cu、Zn 原子间微小的原子半径差异引起的，即几何结构优化后的Te、Cu 原子间距离相对Te、Zn 原子间距离更近一些。

表1 本征ZnTe 与缺陷ZnTe 体系的结构优化晶胞参数Table 1 Optimized lattice parameters of perfect ZnTe and that with defect

ZnTe 结构中，Zn、Te 原子各贡献4 个成键电子形成极性共价键，从2 ×1 ×1 的ZnTe 超晶胞单元中去除中心Zn 原子形成Zn 空位，缺陷使得局部电子密度分布发生变化，这样就造成空缺周围离子结构弛豫，从而改变了缺陷邻近原子之间键长和键强度。

图2(a～c)分别是本征ZnTe、Zn0.875Te 和Zn0.875Cu0.125Te 的电子密度差分图。各图的标尺一致，比较图2(b，c)和图2(a)可以看出，Zn 空位周围Te 原子电荷密度明显降低，掺杂Cu 原子d 轨道电荷密度也很小。这种电荷再分配也可看作是上述晶胞参数变化的微观解释。

图2 本征ZnTe(a)、Zn0.875Te(b)及Zn0.875Cu0.125Te(c)的电子密度差分图。Fig.2 Figures of electron density difference of ZnTe (a)，Zn0.875Te(b)，and Zn0.875Cu0.125Te(c).

3.2 电子结构

本文主要研究了体系的能带结构和态密度［17］。图3(a～c)分别表示ZnTe、Zn0.875Te 和Zn0.875Cu0.125Te 的电子能带结构。图中虚线代表费米能级，即有E -Ef=0.0 eV，能量标准是eV。由图可以看出，3 种体系的价带顶(VBM)和导带底(CBM)均产生在相同的k 点(G)，即都为直接带隙半导体。ZnTe 的带隙计算值约为1.362 eV，比已有实验数据要小［19］，这正是广义梯度近似(GGA)的缺陷所在［20］。

图3 本征ZnTe(a)、Zn0.875Te(b)及Zn0.875Cu0.125Te(c)的电子能带结构图。Fig.3 Electron band structures of ZnTe(a)，Zn0.875Te (b)，and Zn0.875Cu0.125Te (c).

图4(a～c)所示分别是本征ZnTe、Zn0.875Te和Zn0.875Cu0.125Te 晶体的态密度图(DOS)。由图4(a)可以看出，ZnTe 的导带CB 主要来源于Zn的3d 轨道、Te 的5s 轨道及Te 的5p 轨道，其中Zn 原子占主导地位。-13.5～-11.5 eV 之间的价带VB 由Te 的5s 轨道产生，该能带孤立并远离其他频带，因此几乎可以忽略。-7.5～-5.0 eV 之间的价带VB 主要由Zn 的3d 轨道提供。-5.0～0.0 eV 之间的高价带主要由Te 的5p 轨道提供。

与ZnTe 相比，Zn0.875Te 中Te 的5s 轨道转移到高能级范围，如图4(b)所示，空缺轨道出现在费米能级附近，是由Te 原子的未成对孤对价电子引起的。这种差异可能极大地影响到物质的光学性质。据理论计算结果可以预测，Zn0.875Te 中Zn空位可能形成浅受主能级并具有n 型导电性。

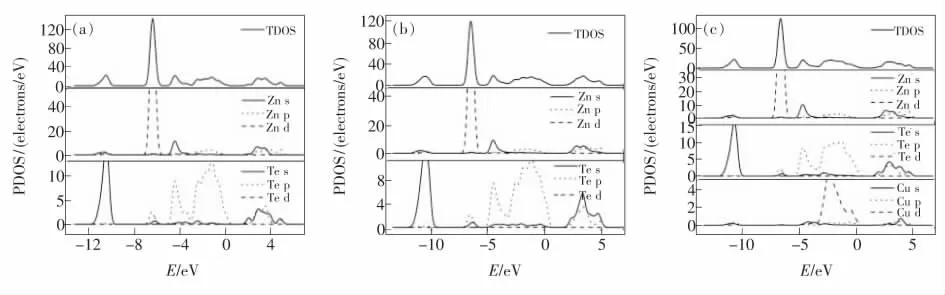
图4 本征ZnTe(a)、Zn0.875Te(b)及Zn0.875Cu0.125Te(c)晶体的总态密度图和各原子的分态密度图。Fig.4 Total and partial state densities of ZnTe(a)，Zn0.875Te(b)，and Zn0.875Cu0.125Te(c).

Zn0.875Cu0.125Te 中Cu 的s 轨道能量与Zn 能量相近，如图4(c)所示，因此Zn0.875Cu0.125Te 与ZnTe可能具有大致相同的能带间隙。能带结构和态密度DOS 表明(图3(c)和图4(c))，Zn0.875Cu0.125Te能带间隙相对较窄(0.960 eV)，价带顶能(EV)上升到0.282 eV 可能是由p-d 排斥作用所引起的［21］:Zn0.875Cu0.125Te 中Cu 的3d 轨道能量相对于Zn 的3d 轨道能量而言，更接近于Te 的4p 轨道的能量，这就产生了更强的p-d 斥力;并且由于Cu 的3d 轨道比Zn 的3d 轨道的离域性更强，因此随之伴有带隙的大幅减小，这使得Zn0.875Cu0.125Te中产生较大的耦合矩阵元，因此会产生更大范围的p-d 斥力，这可能也是掺杂的困难所在。

重叠布居值的大小可用来判断各种价键离子性或共价性的强弱［22］。重叠布居值越高表明共价键相互作用越强，反之离子键相互作用越强，数值的正负则表示成键态与反键态。布居值接近于零，表示这两种原子的电子群体之间为纯离子键相互作用［23］。

由表2 可以看出，3 种体系中Zn—Te 大部分重叠布居数值较高，说明存在共价键。其中有一些表现有混合离子共价键的性质，如Zn0.875Te 中，ZnⅡ(或ZnⅣ)—TeⅠ的重叠部分增加，但键长却减小。这表明Zn 空位诱导了近邻Te 原子的成键的改变，同时，Zn—Te 原子成键中共价键增强，这正与上述电子密度差异分析相吻合。Zn0.875Te 中ZnⅣ—TeⅡ重叠布居数最低，表明共价键减弱。由表2 还可以看出，Zn0.875Cu0.125Te 中Cu—TeⅠ重叠布居数比其他Zn—Te 键要高，这也表明体系的共价键增强。

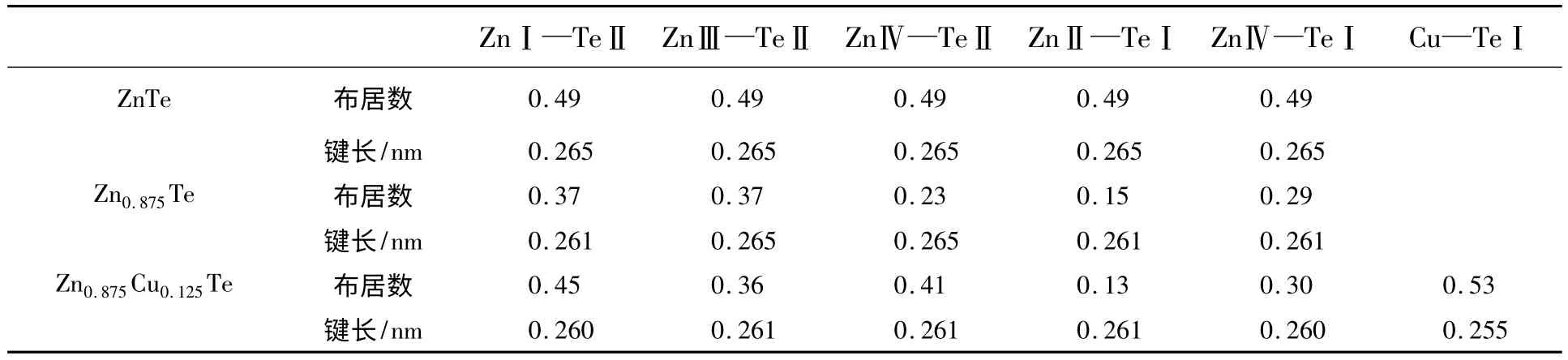
表2 Zn—Te 键与Cu—Te 键的马利肯布居数分析Table 2 Mulliken population analysis on bonds Zn—Te and Cu—Te

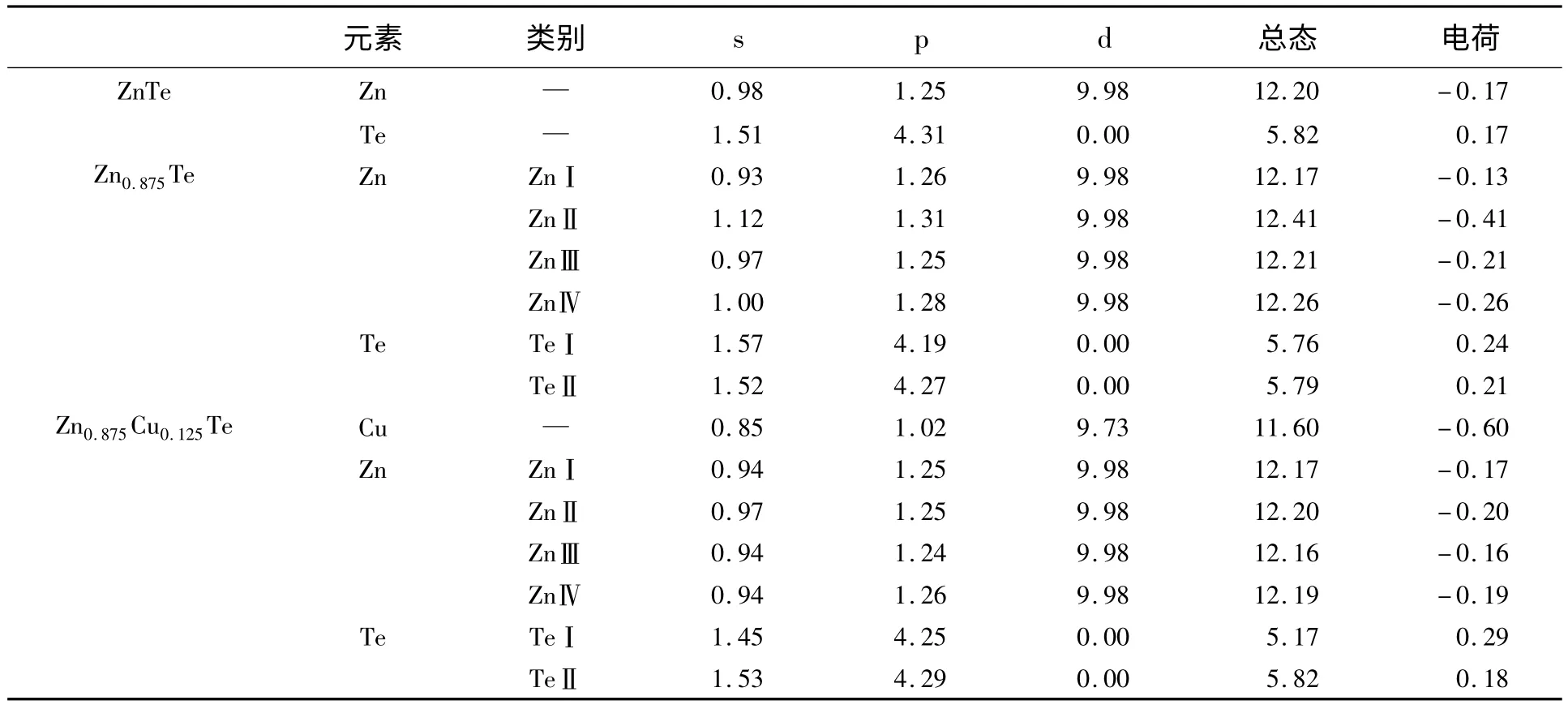
表3 Zn、Te、Cu 原子的马利肯布居数分析Table 3 Mulliken population analysis on atoms Zn，Te，Cu

表3 是体系中3 种原子的马利肯布居数，由表可以看出，同一原子的原子位置不同其电荷分布也不同。

在Zn0.875Te 中，TeⅠ比TeⅡ电荷值下降要稍微多一些。ZnⅠ原子的电荷值增加，但ZnⅡ原子的电荷值却降低，这可能是Zn 空位使得Te 原子产生未配对价电子引起的，从ZnⅡ的s 轨道电子异常排布也可以看出来。对Zn0.875Cu0.125Te 而言，TeⅠ电荷值变化较大，Cu 的电荷值为负值(-0.60e)，表明Cu 的电负性大于Zn，更难失去电子。显然，Zn0.875Te 和Zn0.875Cu0.125Te 中，ZnⅡ原子的电荷值总是最小的，这表明ZnⅡ的位置对Zn 空位或掺杂原子具有最敏感的反应，并且与其他临近原子的相互作用也自发很弱。

3.3 光学特性

这3 种物质在光电子器件与半导体产业方面具有潜在的应用价值，因此它们的光学特性显得尤为重要［2-3］。我们采用剪刀算符来修正带隙，研究了3 种体系的介电函数、损失函数、吸收系数、光电导率、复折射率及反射率［14］。

图5(a～c)是3 种体系的介电函数。由图5(a)可知，ZnTe 的介电函数的虚部ε2(ω)有一个显著的峰:A(4.245 eV)。该峰主要来源于Zn3d和Te4p 轨道价带(VB)向Te4p 和Zn4s 轨道导带(CB)的过渡，这由图3(a)中的局部密度的状态也可以看出。Zn0.875Te 在0.496 eV 处产生了一个新峰(B)，如图5(b)所示，这可能是由电子从导带向空位受体能级转换并引起红色光致发光引起的。同样，如图5(c)所示，Zn0.875Cu0.125Te 的介电峰C(0.865 eV)也可能是由于电子从导带向杂质受主能级转变引起的。

图5 本征ZnTe(a)、Zn0.875Te(b)及Zn0.875Cu0.125Te(c)晶体的介电函数。Fig.5 Dielectric function of ZnTe(a)，Zn0.875Te (b)，and Zn0.875Cu0.125Te(c).

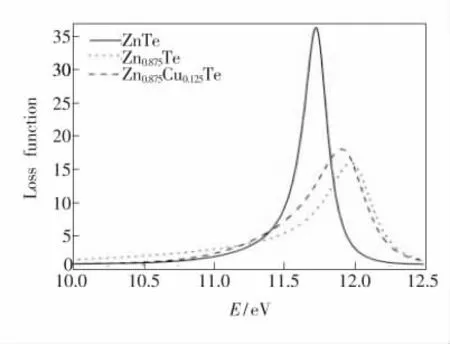
图6 本征ZnTe、Zn0.875Te 及Zn0.875Cu0.125Te 晶体的损失函数。Fig.6 Loss function of ZnTe，Zn0.875Te，and Zn0.875Cu0.125Te.

由电子能量损失函数与介电常数的关系式(5)可以得到体系电子的能量损失函数。图6 所示为3 种体系的电子能量损失函数。由图可以看出，当ZnTe 体系能量小于0.693 eV 时，能量损失为0。ZnTe、Zn0.875Te 和Zn0.875Cu0.125Te 的损失峰分别出现在11.727，11.975，11.910 eV 处，能量损失分别为35.258，15.889，17.927 eV，分别与等离子体振荡直接相关并对应于边缘能量。

图7 是相应的线性吸收谱图。ZnTe 从0.16 eV 开始出现吸收峰，与实验结果符合较好［19］，这主要是由电子从Te4p 轨道价带顶过渡到Zn3d 轨道导带底引起的，每一个吸收峰的能量也几乎是由激发电子从价带向导带跃迁引起的。显然，吸收峰表明Zn0.875Te 和Zn0.875Cu0.125Te都产生红移。

光电导效应是半导体各种光电子作用的物理基础［14］。图8 是3 种体系的复光电导率，由图8(a～c)可以看出:ZnTe、Zn0.875Te 和Zn0.875Cu0.125Te 3种体系的实部分别在能量小于0.4 eV 和大于16.6 eV的范围内、能量大于16.8 eV 的范围内以及能量大于16.8 eV 的范围内为0，主要峰值分别出现在3.7～5.3 eV、3.8～5.3 eV 和3.8～5.3 eV 的范围内，与吸收峰出现的范围相一致，说明光电导率实部与吸收系数之间存在着密切的关系。

图7 本征ZnTe、Zn0.875Te 及Zn0.875Cu0.125Te 晶体的吸收系数。Fig.7 Absorption coefficients of ZnTe，Zn0.875Te，and Zn0.875Cu0.125Te.

图8 本征ZnTe(a)、Zn0.875Te(b)及Zn0.875Cu0.125Te(c)晶体的光电导率。Fig.8 Photoconductivity of ZnTe(a)，Zn0.875Te(b)，and Zn0.875Cu0.125Te(c).

图9 本征ZnTe(a)、Zn0.875Te(b)及Zn0.875Cu0.125Te(c)晶体的复折射率。Fig.9 Complex refractive index of ZnTe(a)，Zn0.875Te(b)，and Zn0.875Cu0.125Te(c).

由介电函数与复折射率的关系式(7)和(8)可得到3 种体系的复折射率。由图9 可知，ZnTe、Zn0.875Te 和Zn0.875Cu0.125Te 的折射率n 的主要峰值分别出现在1.6～3.8 eV、2.9～3.9 eV 和1.9～3.7 eV的范围内，最大峰值对应能量分别为1.8，3.4，2.7 eV。由图5 可知，3 种体系的介电函数的实部(Re)分别在能量为4.4～11.7 eV、4.5～11.9 eV 和4.5～11.9 eV 的范围内为负值，在此范围内光反射率很大，光不在固体中传播。由图7 可以看出，3 种体系分别在光子能量小于0.3 eV 和大于16.4 eV 的范围内、大于17.9 eV的范围内以及大于17.8 eV 的范围内对光的吸收为0，表明分别在波长小于4.6 nm 和大于273.3 nm 的范围内、小于0.2 nm 的范围内以及小于0.2 nm的范围内是透明的，即与吸收系数相对应。

图10 本征ZnTe、Zn0.875Te 及Zn0.875Cu0.125Te 晶体的反射率。Fig.10 Reflectivity of ZnTe，Zn0.875Te，and Zn0.875Cu0.125Te.

根据关系式(9)，由体系的复折射率可进一步计算体系的反射系数。图10 是3 种体系的反射谱，由图可以看出，ZnTe、Zn0.875Te 和Zn0.875Cu0.125Te 分别在1.4～4.651 eV、1.4～4.5 eV 和1.4～4.8 eV的能量范围内发生部分反射现象，而在6.3～12.8 eV、6.4～13.0 eV 和6.5～13.0 eV 的高能区域内，其平均反射率分别达到了0.669、0.587和0.634。当能量分别为8.286，8.438，8.389 eV时，其反射率达到最大，分别为0.808、0.789 和0.801，均接近于1，说明此能量范围内体系均能呈现出金属反射特性，入射的光大部分被反射。由图9 也可以看出，在对应能量范围内，折射率值n 趋近于0，说明Zn、Cu 的4s 电子与Te 的5p 电子之间具有很深的能级，这与上述能带结构和态密度结果也相吻合。

4 结 论

采用基于密度泛函理论下的平面波赝势法(PWP)及广义梯度近似(GGA)，研究了闪锌矿ZnTe 结构本体及缺陷掺杂体系Zn0.875Te 和Zn0.875Cu0.125Te 的电子结构和光学性质。计算获得的结果与其他理论结果及已有实验数据吻合较好。相对于ZnTe 结构本体而言，由于有缺陷的存在，Zn0.875Te 和Zn0.875Cu0.125Te 体系的晶格参数略有变化，晶体体积略有减小，原子的电荷量也因为成键性质的变化而产生了一定的改变，这两种受主能级价带顶都提供了n 型电导性。由于缺陷能级的引入，体系带隙减小。对于Zn0.875Cu0.125Te，价带顶的p-d 排斥作用及导带底的sp 杂化还有助于带隙变窄，电子也因此在可见光区的跃迁明显增强。Zn0.875Te 和Zn0.875Cu0.125Te 均出现了介电峰，吸收光谱产生一定程度的红移，改善了ZnTe 的光学性质。

［1］Xia Z Q，Li R P.First principles study of rare earth doped in ZnTe used for CdTe solar cell back contact layer［J］.Acta Phys.Sinica (物理学报)，2012，61(1) ：0171081-071086 (in Chinese).

［2］Kim J S，Kim H M，Park H L，et al.Growth and optical characterization of single quantum well structure of submonolayer ZnS/ZnTe［J］.Solid State Commun.，2006，137(3) ：115-119.

［3］Erlacher A，Ambrico M，Perna G，et al.Absorption and photoconductivity properties of ZnTe thin films formed by pulsedlaser deposition on glass［J］.Appl.Surf.Sci.，2005，248(1-4) ：402-405.

［4］Joshi K B，Pandya R K，Kothari R K，et al.Electronic structure of BeTe and ZnTe［J］.Phys.Status Solidi (b)，2009，246(6) ：1268-1274.

［5］Zhou X H，Chen X S，Huang Y，et al.First-principles study of carrier-mediated ferromagnetism in ZnTe-based thin film［J］.Phys.Stat.Sol.(b)，2006，243(6) ：1375-1382.

［6］Szwacki N G，Przez＇dziecka E，Dynowska E，et al.Structural properties of MnTe，ZnTe，and ZnMnTe［J］.Acta Phys.Pol.(a)，2004，106(2) ：233-238.

［7］Uspenskiia Y，Kulatovb E，Mariettec H，et al.Ab initio study of the magnetism in GaAs，GaN，ZnO，and ZnTe-based diluted magnetic semiconductors［J］.J.Magn.Magn.Mater.，2003，258-259：248-250.

［8］Tablero C.Acceptor and donor ionization energy levels in O-doped ZnTe［J］.Comput.Mater.Sci.，2010，49(2) ：368-371.

［9］Segall M D，Lindan P J D，Probert M J，et al.First-principles simulation：Ideas，illustrations and the CASTEP code［J］.J.Phys.：Condens.Matter.，2002，14(11) ：2717-2744.

［10］Liu X，Furdyna J K.Optical dispersion of ternary Ⅱ-Ⅵsemiconductor alloys［J］.J.Appl.Phys.，2004，95(12) ：7754-7765.

［11］Han D，West D，Li X B，et al.Impurity doping in SiO2：Formation energies and defect levels from first-principles calculations［J］.Phys.Rev.B，2010，82(15) ：155132-155138.

［12］Guo L，Hu G，Zhang S T.Defects energetic，electronic structure and optical properties of Cu-doping and Zn vacancy impurities in ZnSe［J］.Acta Phys.-Chim.Sinica (物理化学学报)，2012，28(1) ：1-9 (in English).

［13］Zhang Z Y，Yang D L，Liu Y H，et al.Electronic structures and optical properties of BaTiO3［J］.Acta Phys.-Chim.Sinica (物理化学学报)，2009，25(9) ：1731-1736 (in Chinese).

［14］Zhao F J，Xie Q，Chen Q，et al.First principles calculation of BaSi2electronic structure and optical properties［J］.Science in China (Series G：Physics，Mechanics ＆ Astronomy) (中国科学G 辑：物理学 力学 天文学)，2009，39(2) ：260-266 (in Chinese).

［15］Feng J，Xiao B，Chen J C，et al.Optical properties of new photovoltaic materials：AgCuO2and Ag2Cu2O3［J］.Solid State Commun.，2009，149：1569-1573.

［16］He K H，Yu F，Ji G F，et al.Study of optical properties and electronic structure of V in ZnS by first principles［J］.Chin.J.High Pressure Phys.(高压物理学报)，2006，20(1) ：56-60 (in Chinese).

［17］Li J H，Zeng X H，Ji Z H，et al.Electronic structure and optical properties of Ag-doping and Zn vacancy impurities in ZnS［J］.Acta Phys.Sinica (物理学报)，2011，60(5) ：0571011-1-7 (in Chinese).

［18］Reuter K，Stampfl C，Scheffler M.Handbook of Materials Modeling：Part A Methods［M］.Berlin：Springer，2005，149-234.

［19］Gao H X，Xia J B.Effect of Li-doping on the magnetic properties of ZnO with Zn vacancies［J］.J.Appl.Phys.，2012，111(9) ：093902-1-5.

［20］Muscat J，Harrison N M，Thornton G.First-principles study of potassium adsorption on TiO2surfaces［J］.Phys.Rev.B，1999，59(23) ：15457-15463.

［21］Wei S H，Zunger A.Role of metal d states in Ⅱ-Ⅵsemiconductors［J］.Phys.Rev.B，1988，37(15) ：8958-8981.

［22］Mulliken R S.Electronic population analysis on LCAO-MO molecular wave functions［J］.J.Chem.Phys.，1955，23(10) ：1833-1840.

［23］Segall M D，Shah R，Pickard C J，et al.Population analysis of plane-wave electronic structure calculations of bulk materials［J］.Phys.Rev.B，1996，54(23) ：16317-16320.