非线性功放信道下联合信道估计研究

孙珊珊，孙学斌，李 斌，周 正

(北京邮电大学信息与通信工程学院，北京 100876)

0 引言

在无线通信系统中，非线性放大器广泛存在于无线信道中，对数据的传输与恢复、相关检测和信道均衡等等有着显著的影响。因此，在做一些信道相关的应用和研究时，有必要研究一些信道特性，包括非线性放大器的参数和信道参数的估计。现有的信道估计方法没有针对非线性放大器的参数进行估计，本文针对因非线性放大器产生非线性影响的FIR信道，对非线性放大器的参数进行了估计，对输入信号进行了检测［1］。

盲均衡技术指的是在非线性放大器及信道参数未知的情况下，通过被非线性和噪声污染的输出信号(观测信号)来检测输入信号。根据贝叶斯方法来估计非线性放大器的参数。MCMC［2］是贝叶斯方法的一种，依托于贝叶斯框架，利用先验信息提高解的精度，同时没有对贝叶斯理论进行线性化，适合于存在非线性放大器的高斯信道。MCMC方法通过构造一个平稳分布于所求后验分布相同的马尔科夫链，反复迭代至平稳状态，从而得到后验分布的样本，再基于这些样本做各种统计推断，就可以获得模型均值及其对应的方差，从而得到非线性放大器的参数估计值并检测信号参量。

目前，现有的算法中并没有对存在非线性放大器的信道进行多种非线性参数的联合估计，因此需要一种应用于无线通信系统的存在非线性放大器的联合非线性参数估计和信号检测的方法。这里采用的Metropolis-Hastings(MH)算法是MCMC方法的一种，针对本发明的应用场景，进行非线性放大器的非线性参数估计和输入信号的检测［3］。

1 信道模型

硬件的非理性因素会造成一定的硬件减损，对通信性能产生较大影响。硬件减损主要包括功率放大器(Power Amplifier，PA)的非线性影响。PA的非线性影响包括幅度失真(AM-AM)和相位失真(AMPM)［4］。在60 GHz信道中功率放大器的非线性模型如下:

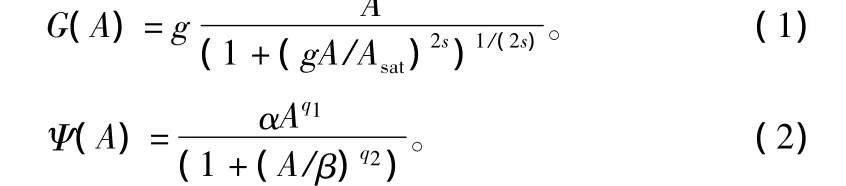
式中，A和G(A)分别为输入和输出的电压幅度;线性增益g=4.65;失真拐点平滑程度s=0.81;输出电压幅度饱和值Asat=0.58 V;Ψ(A)为输入电压幅值为A时所产生的相位失真大小，单位为角度制;α，β，q1，q2的取值分别为 2560，0.114，2.4，2.3。由式(1)和式(2)可知，输入信号幅度越大，幅度失真和相位失真就越严重。经过16QAM编码调制的数据流{dπ(i)}，经过非线性放大器后变成{xk}，接着进入单径信道，信道模型如下:

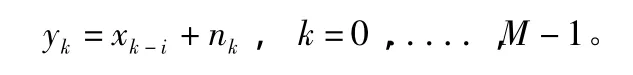
式中，yk，xk和nk互相独立，分别为k时刻的接收信号、传输信号和加性噪声。采用的存在非线性功放下的单径系统模型如图1所示。

图1 存在非线性放大器系统

2 MCMC算法

MCMC是贝叶斯方法的一种，它通过反复迭代以构建马尔科夫链至平稳状态，最后可以获得目标分布的样本，使得许多复杂的贝叶斯分析问题得到解决。它是对非线性参数进行估计的关键部分，经过反复迭代在这一模块中得到非线性放大器的非线性参数［5］。MCMC方法就是通过建立一个平稳分布为π(x)的马尔科夫链来得到π(x)的样本，并根据这些所得到的样本做统计推断，可用如下步骤来描述:

建立一个转移核P(·，·)的马尔科夫链，其平稳分布为π(x)，常用的构造转移核的是Gibbs抽样和Metropolis-Hastings方法。

从X(0)出发，根据式(1)中的马尔科夫链生成X(1)，…，X(n)。

当生成的链的长度足够时，

可用来表示函数f(x)的期望值。

由于 Metropolis-Hastings［6］方法非常适合本发明中的条件，因此这里采用 Metropolis-Hastings方法。

假设目标是从目标密度函数p(θ)(∞ ＜θ＜∞)中得到采样粒子［7］。由 Metropolis-Hastings(MH)方法采样建立的马尔科夫链产生一系列的值θ(1)→θ(2)→…+→θ(t)→…，在这里 θ(t)表示马尔科夫链在t时刻收敛得到的值。在Metropolis-Hastings方法中，先初始化最初状态，θ(0)是初始值，该取值最好接近真实值，不要离得过远。然后根据采样器先前的状态，利用提议概率分布q(θ|θ(t－1))产生一个候选值θ*。下一步就是根据接受概率α，选择接受或拒绝候选值［8］，

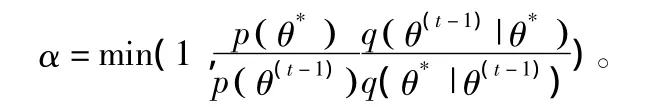
先产生一个随机数u(0＜u＜1)，如果u＜α，则接受这个候选值θ(t)=θ(*)，否则拒绝这个候选值，一直产生新的候选值，直到达到收敛。

为了解决本发明中的问题，让未知参量组成一个向量，并且它们的目标概率分布是已知的。不是整体更新 Θ 值，而是依次更新 Θ =［θ1，θ2，θ3…θn］T中的每一个参数。先将向量初始化 Θ0=［，］T，让 Θ－i=［θ1，…，θi－1，θi+1，θn］，Θ－i包含了除了θi的所有其他θ。

选择循环平稳随机游走函数作为核函数qi=(|，Θ－i)针对本发明中的问题，核函数选择:

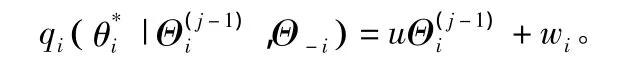
式中，u是一个常数，(0＜u＜1);wi在本发明中为正态分布。

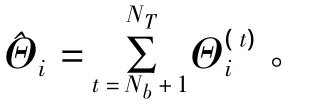
基于MCMC技术的对存在非线性功放的单径信道的联合信道估计及数据检测方法具体步骤［9］归纳如下:

① 发送端产生随机二进制序列 { di}，经过16QAM编码调制形成数据流{dπ()}i;接着，该数据流经过功率放大器变为{xk}，最后进入单径信道，接收机从信道接收到观测数据{yk}。

②设迭代系数j=1，构造参数向量并进行初始化。

式中，Θ向量中的各参数对应于非线性功放模型中各非线性参数 g，s，As，q1，q2，alfa，beta。

③设参量系数i=1，参数向量的第i个可能值φi由随机游走概率密度函数，Θ－i)得到。本步骤是本发明方案中最关键的一步，要找到合适的随机游走函数，使得马尔科夫链的极限分布是目标函数分布。在本发明中，目标函数分布［10］为:

根据目标函数所取的随机游走函数为:

在这里wi是符合均值为 u·，方差为1/u的高斯分布。

④ 计算接受概率 αi，Θ－i，φi)。

⑤产生一个在区间［0，1］上均匀分布的随机数u，令

⑥更新参量系数i到i+1，然后回到步骤③。当i=7时，到步骤⑦。

⑦更新收敛系数j到j+1，然后回到步骤②。当达到收敛或设定的收敛值时结束循环。

⑧取均值，除去收敛之前得到的估计值，将收敛后得到的估计值取均值。

式中，NT为总的收敛次数;Nb为需要去除的前面不收敛的次数。

⑨利用得到的非线性功放参数和信道参数，利用最小差值法进行数据检测［11］。

3 仿真结果

仿真获得的非线性放大器产生的非线性模型中，各个非线性参数估计值与实际值对比如图2和图3所示。由图形可以看出，仿真得到的估计值与真实值相差较小，并且收敛速度很快，大约50次左右就可以达到收敛。

图2 g，s，Asat，q1 的估计值与真实值的对比

图3 q2，alfa，beta的估计值与真实值的对比

在得到模型中各非线性参量的估计值后，利用最小差值法进行数据检测，得到数据检测值的误码率随BER变化的仿真图如图3(d)所示，在信噪比为16 dB时得到误码率为10－5，效果良好。

4 结束语

首先分析了存在非线性放大器的单径信道模型，对MCMC技术中的MH算法进行了详细地描述，然后提出了基于MCMC算法的联合信道估计和信号检测技术，最后针对所提算法进行了仿真。

所提出的算法适用于所有已知非线性模型的信道，在非线性放大器及信道参数未知的情况下，通过被非线性和噪声污染的输出信号(观测信号)来估计非线性放大器的参数，经过反复迭代可以估计出所有的未知参数。仿真结果表明，将MCMC算法应用于非线性参数估计和信号检测中，有优越的检测性能。 ■

［1］YANG Li-ly.60GHz:Opportunity for Gigabit WPAN and WLANConvergence ［J］.ACMSIG-COMM Computer Communication Review，2009，39(1):56 －61.

［2］HERZET C，WYMEERSCH H，MOENECLAEY M，et al.On Maximum-likelihood Timing Synchronization，2007，55(6):1116－1119.

［3］GUENACH M，WYMEERSCH H，STEENDAM H.，et al.Code-aided Ml Joint Synchronization and Channel Estimation for Downlink MC-CDMA，2006，24(6):1105 －1114.

［4］TANNER M A.Tools for Statistics Inference［M］.New York:Springer-Verlag，1991.

［5］ROBERT C R，CASELLA G.Monte Carlo Statistical Methods［M］.New York:Springer，1999.

［6］DOUCET A，WANG X.Monte Carlo Methods for Signal Processing:a Review in the Statistical Signal Processing Context，2005，22(6):152 －170.

［7］RITTER C，TANNER M A.Facilitating the Gibbs Sampler:the Gibbs Stopper and the Griddy Gibbs Sampler［M］.Journal of the American Statistical Association，1992(87):861－868.

［8］GILK S.Richardson，Introducing Markov Chain Monte Carlo［M］.In Markov Chain Monte Carlo in Practice.London:Chapman ＆ Hall，1996.

［9］SUYAMAS，SUZUKI H，FUKAWA K，et al.Iterative Receiver Em-ploying Phase Noise Compensation and Channel Estimation for Millimeter-Wave OFDM Systems［J］.IEEE Journal on Selected Areas in Communications，2009，27(8)，111 －115.

［10］FARHANG B，ZHU H，SHI Z.Markov Chain Monte Carlo Algorithms for CDMA and MIMO Communication Systems［J］.IEEETrans.Signal.Process，2006，54(5):1896 －1909.

［11］FRANK H，FRISCH I T.Analysis and Design of Survivable Network［J］.IEEE Transactions on Communication Technology，1970，218(5):501－519.