基于射表数据的火炮弹道仿真分析方法

胡梦中，衣同胜，潘佳梁，潘朝晖

(中国人民解放军92941部队，辽宁葫芦岛 125000)

0 引言

由于空气阻力对高速的火炮弹道具有重要影响，实际试验过程中，人们特别期望能在计算其弹道之时能合理考虑空气阻力的影响，获取高精度的弹道仿真数据，从而为测控装备跟踪拦截火炮目标提供指导，查阅相关文献［1－10］可知，空气阻力的大小与目标形状、速度和气象参数等有着复杂的关系，合理建立完备的数学模型十分困难。在分析诸多影响空气阻力的因素之中可以发现，目标形状和速度是影响其受空气阻力的主要因素。

由于难以建立精确的数学模型考虑空气阻力，人们在试验过程中常常注重积累一些常用射角下的火炮射表数据以便火炮弹道估算之用，本文正是基于这些珍贵的射表数据，结合现有的空气阻力理论模型，从速度及形状这2个主要影响因素来建立一种空气阻力模型，从而实现火炮弹道的精确计算。

1 基于射表数据空气阻力模型的建立

火炮射表数据一般指火炮在某一特定发射俯仰角下，火炮在不同时间点对应的空间位置数据，一般包括:时间、对应时间点火炮斜距和对应时间点火炮高程。

假设火炮射表数据包括以上3个方面，通过坐标转换及数据分析，可以得出火炮发射后水平和垂直方向的加速度，由于火炮在空中只受重力和空气阻力的影响，重力为垂直方向，空气阻力可以分解到水平和垂直方向，故可利用多项式拟合得出火炮所受到的空气阻力与速度的关系式，具体数据处理流程如图1所示。

图1 火炮射表数据处理流程

上述涉及的多项式拟合，可分别采用1阶、2阶和3阶多项式拟合法得到阻力在水平及垂直方向上产生的加速度函数，结合文献［1－7］已有的空气阻力模型，分析比较发现采用2阶多项式拟合能较好地反映加速度与速度的关系，设拟合后加速度计算公式为:

设火炮发射后初速度在水平及垂直方向分量分别为Vx0和Vy0，由于在垂直方向上火炮受到阻力和重力的影响，在水平方向上火炮只受空气阻力影响，发射后火炮加速度及速度计算公式为:

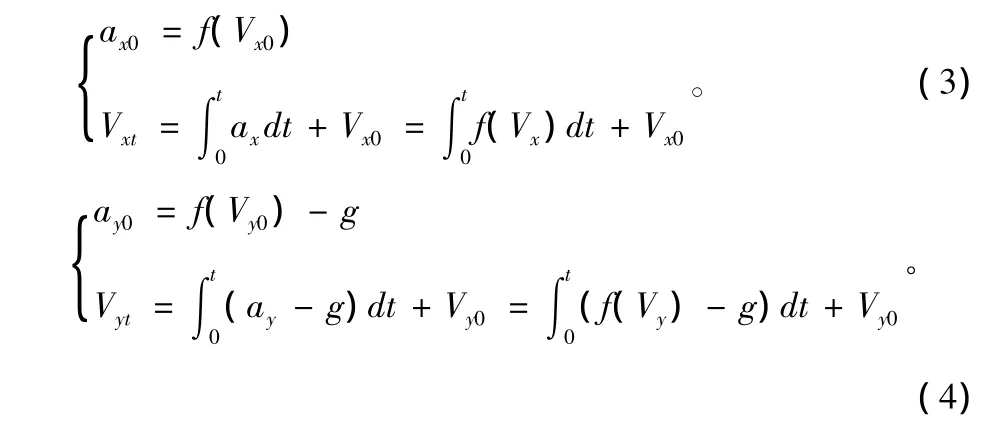
式中，g为重力加速度，将式(1)和式(2)代人式(3)和式(4)就得到火炮瞬时加速度计算公式，然而实际上，式(3)和式(4)中Vx，Vy也是一个与时间有关的函数，且并不知其具体表达式，故积分无法得出解析表达，分析发现可以采用时间离散分析得出离散化的计算结果。

2 火炮弹道离散分析与计算

以上提到Vx实际上也是一个与时间有关的函数，无法得到具体表达式，但可以将上述积分离散化进行分析。假设需要分析0～T时间内火炮的弹道，首先，可以将时间以步长为Δt离散化，并假设在各离散化时间单元内，火炮受到的空气阻力不变，则在t=Δt时加速度:

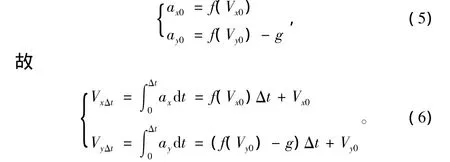
在t=Δt时目标在水平及垂直方向的飞行距离为:

同理可得t=2Δt时目标水平及垂直方向的飞行距离为:

依次类推可得t=nΔt时，

故在t=nΔt时目标在水平及垂直方向的飞行距离为:

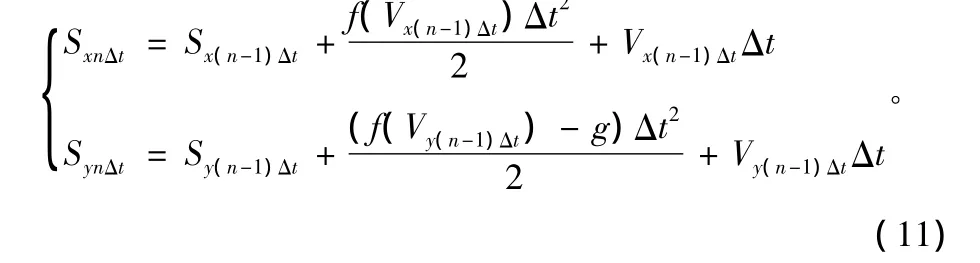
通过以上递推公式，可以计算出离散时间点目标的空间位置，实现弹道的计算。需要注意以下几点:

①该方法是通过对火炮射表数据进行处理，进而建立了空气阻力模型，所以射表数据的精度对计算结果具有重要影响;

②该方法实际只需1个俯仰角度的射表数据就能建立完整的空气阻力模型，进而进行任意俯仰角度的火炮弹道分析计算，但为了充分考虑目标形状与姿态对空气阻力的影响，可以通过收集火炮在不同发射俯仰角下的射表数据，调用对应俯仰角的射表数据进行分析计算，提高分析精度;

③以上建立的火炮弹道计算方法需要火炮发射时的初速度，进而实现后续的递推计算，所以火炮发射时初速度的精度对弹道计算精度具有一定影响;

④由于气象参数对目标受到的阻力也具有一定影响，若需更为精确的建立空气阻力模型，可以考虑积累不同气象参数条件下目标的射表数据，再利用本文提出的方法实现进一步的精确建模。

3 仿真试验与分析

3.1 空气阻力的加速度与速度关系仿真分析

利用本文方法，仿真研究某一火炮加速度与速度的关系，采用了2阶多项式拟合由分析射表数据而得到的数据，比较结果如图2和图3所示。

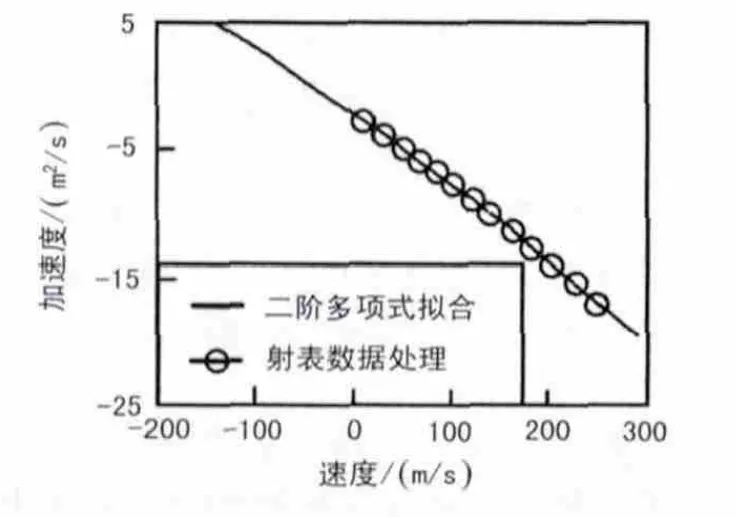
图2 水平方向加速度与速度关系

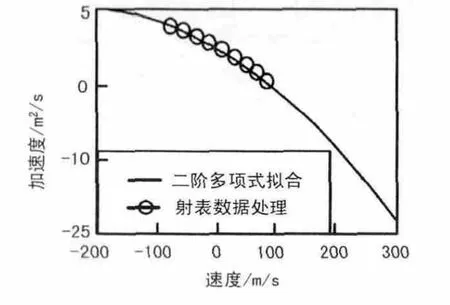
图3 垂直方向加速度与速度关系

可以看出拟合后的曲线与射表数据吻合良好，而且能较好地反应出空气阻力产生的加速度与速度关系，符合现行空气阻力与速度关系的一次函数及二次函数的空气阻力模型分析结果，进一步分析可以得出以下结论:

①在水平与垂直方向上空气阻力产生的加速度与速度关系有所不同，水平方向呈现出二次函数关系，垂直方向呈现一次函数关系，分析原因可能由于火炮在水平及垂直方向上形状不同所致;

②由于拟合后的函数符合现行空气阻力模型，故拟合后所得的关系式能较好地预测射表数据中速度范围以外的加速度变化，故可用于分析火炮不同俯仰角发射时加速度的计算;

③由于不同俯仰角下目标在水平及垂直方向上形状会有一些不同，空气阻力变化趋势也会有些不同，所以在实际分析时，尽可能采用接近待分析的火炮俯仰角的射表数据的拟合结果来进行加速度的准确计算;

④由图2、图3可以明显看出空气阻力产生的加速度比较大，特别是火炮发射后速度非常大的一段时间内空气阻力产生的加速度约为重力加速度的4倍，可见空气阻力的影响在速度很大时已远超过重力的影响。

3.2 与原始射表数据及抛物线法的比较与分析

选择火炮俯仰角为6°时的射表数据，采用本文提出的方法及抛物线法分别计算火炮弹道，并与射表原始数据进行比较，如图4所示。

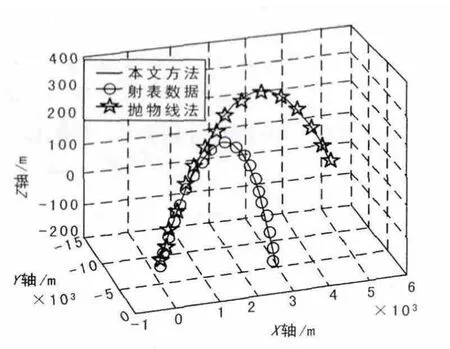
图4 俯仰角为6°时火炮弹道仿真比较

由图4可知:①本文提出的方法计算结果与射表原始数据完全一致，证明了本文方法的正确性与有效性;②抛物线法是一种完全不考虑空气阻力影响的方法，可以看出本文提出的计算方法在考虑空气阻力后的弹道与未考虑空气阻力影响的火炮弹道在发射开始段有部分重合，但一段时间后2个弹道相差甚远，可见不考虑空气影响的抛物线法根本无法用于火炮的全程弹道计算。

4 结束语

通过对火炮射表数据分析处理研究，建立了一种基于射表数据的空气阻力模型，通过时间离散分析，最终实现了考虑空气阻力影响下的火炮弹道的有效数值计算。针对如何考虑目标形状及气象参数对空气阻力的影响建立更为精确的计算模型问题，给出了后续研究及工作的建议。目前，该方法已成功地应用于火炮试验中弹道的高精度仿真分析，多次为测控装备的跟踪拦截火炮提供精确的数据支撑，提高了测控装备跟踪捕获火炮弹丸类目标的能力。 ■

［1］杨晓红.浅析理想模型状态下空气阻力的计算［J］.扬州职业大学学报，2005，9(1):28 －31.

［2］冯红宁.空气阻力对于抛物体轨道射程的影响［J］.鞍山师范学院学报，2011，13(6):8 －11.

［3］廖 旭，任学藻，周自刚.非理想抛体的最佳抛射角［J］.大学物理，2007，26(8):20 －21.

［4］喻 莉，杨植宗，何 艳，等.考虑空气阻力的抛体最大射程和最佳抛射角研究［J］.空军雷达学院学报，2010，24(6):452 －453.

［5］闵永林，陈 池.两种空气阻力模型的抛射体飞行轨迹研究［J］.装备制造技术，2009，12(3):15 －17.

［6］贾拴稳.有阻力的空气介质中质点的运动规律［J］.安阳师范学院学报，2008(5):32－34.

［7］施毅敏，曾晓英.空气阻力模型与运动方程的关系研究［J］.衡阳师范学院学报(自然科学)，1999，20(6):96－98.

［8］王福新，李 红.抛体运动最大射程的概括性分析［J］.大学物理，2007，26(10):16 －17.

［9］陈小波，李 强.关于抛体运动的分析［J］.四川文理学院学报(自然科学版)，2009，19(5):25 －28.

［10］丁增平.由抛体运动的解题思路探究一题多解［J］.安庆师范学院学报(自然科学版)，2009(3):127－128.