基于Simulink的直扩系统频域窄带干扰抑制研究

刘艳良，孔军辉，刘海见

(海军大连舰艇学院基础部，辽宁大连 116018)

0 引言

窄带干扰是DSSS系统所面临的最常见干扰，它是一种干扰频带相对于有用信号窄得多的干扰形式。DSSS系统虽然对窄带干扰具有一定的抑制作用，但在窄带干扰功率足够大、干扰特性复杂或者干扰频率为系统载波的中心频率时，系统接收机将无法正常完成解扩和解调等工作。由于DSSS系统的处理增益不能无限地增大，因此必须依靠窄带干扰抑制技术在接收机解扩前，对窄带干扰进行处理清除［1］。

干扰抑制的基本思想就是采取措施在直扩信号解扩之前把强干扰能量消除，不让强干扰进入解扩解调器，避免干扰超出DSSS系统的干扰容限。目前常用的干扰抑制技术主要分为基于时域预测的干扰抑制技术与变换域干扰抑制技术［2，3］。在变换域干扰抑制技术中，最常用且易于工程实现的是基于FFT的干扰抑制算法，其不需要逐步收敛的过程，并且可以通过快速算法来实现，因此处理速度远远超过时域滤波技术。下面利用Matlab的可视化工具Simulink构建直接序列通信系统模型，仿真分析了基于FFT的干扰抑制技术的有效性，为直接序列扩频系统在干扰环境下的应用提供了依据。

1 基于FFT的干扰抑制算法

1.1 基本原理

在扩频通信系统中，基于FFT的窄带干扰抑制算法的基本原理是利用窄带干扰与扩频信号频域特性的不同，先将混合信号变换到频域，由于窄带干扰相对于扩频信号频域上表现为很窄的尖峰，可以通过包络检测生成门限进行陷波处理，将高于门限值的谱线衰减或完全去除，最后反变换还原成时域信号进行解扩解调处理，从而达到抑制干扰的目的。基于FFT的干扰抑制原理及处理过程中的信号频谱如图1所示。

图1 基于FFT的干扰抑制原理与信号频谱

从图1可以看出，在频域干扰抑制处理过程中，必须在做FFT运算前对时域信号序列进行加窗处理［4］，若不加窗就相当于对时域信号加了矩形窗。由于矩形窗函数的傅里叶变换为sinc函数，其第一旁瓣比主瓣低13.46 dB，对于比有用信号大几十分贝的窄带干扰来说，它的旁瓣也比信号大很多，这样就不可避免地造成了干扰信号的频谱泄露。因此，在进行干扰抑制时，就会使得干扰消除不彻底，或者是增大了消除的带宽范围，因而加重了对有用信号的损伤［5］。为了减小干扰的频谱泄露，必须采用低旁瓣的窗函数，如切比雪夫窗或布莱克曼窗等。

1.2 干扰门限生成算法

为了保持门限确定的自适应性，通常根据当前一次或几次FFT变换值来确定门限值。门限的确定可以表示为［6］:

式中，Thmin为最小的门限值，通常指没有干扰信号时的幅度值;M为FFT变换的次数;NFFT为FFT变换的长度;η为衰减的系数;um为输入信号x(n)和窗函数w(n)相乘之后的FFT变换的值，即

干扰门限确定之后，对超过干扰门限值的谱线通常认为是含有干扰的谱线，可对这些谱线置零，将其彻底去掉，从而实现了频域的陷波处理［7］。

1.3 重叠复用处理

在频域干扰抑制处理过程中，在对信号分段进行FFT变换前加窗是一个很重要的环节。从时域来看，加窗实质上是对输入数据进行加权处理，保证了在FFT之前数据段两端的平滑，虽然达到了减小频谱泄露的目的，却使输入信号发生畸变，带来了额外的信噪比损耗。通常减小加窗损耗的措施是对数据进行重叠加窗，这样既可以补偿由于加窗带来的处理增益损失，又可以增强信号的关联性。假设分段数据长度为N，重叠的比例因子为r(0＜r＜1)［8］。重叠复用原理如图2所示。

图2 重叠复用原理

由图2可知，重叠复用处理必须增加数据若干路处理通道，将每路信号边缘由于加窗而扭曲较大的信号抛弃，保留中间损失较小的信号，将各路信号合成之后即可减小对原信号的扭曲程度。一般重叠比例越大，加窗引起的信噪比损耗就越小，但计算量将随之增大。所以，通常根据实际的性能要求和硬件条件来确定重叠比例的选择。

2 干扰抑制模块的设计及仿真

2.1 仿真模型构建总体思路

利用Matlab的可视化工具Simulink可以方便地建立系统的可视化模型，使得仿真系统建模与工程中的方框图统一起来，并且通过可视化模块近乎“实时”地将数据输入输出显示出来，使得系统仿真工作大为方便、快捷［9］。根据以上分析，采用1/4重叠加窗处理的干扰抑制模型原理如图3所示，其中，x(n)为含窄带干扰的信号;y(n)为经过干扰抑制后的输出信号，均为采样后的离散信号，采样点数为N。

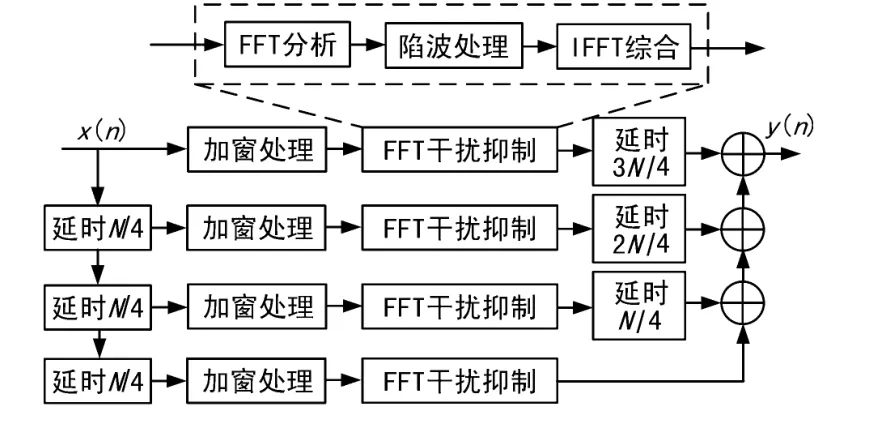
图3 1/4重叠加窗和干扰抑制原理

图3中干扰抑制采用基于FFT的频域陷波处理技术，其原理如图4所示，其中，W(n)为窗函数;abs(u)和angle(u)两个函数分别求FFT变换后的幅度和相位值;Th(u)函数用于确定干扰抑制的门限值;P(u)函数是对超出门限值的谱线进行衰减处理［10］。

根据式(1)构建的干扰门限生成原理及大谱线处理方法如图4中虚线框中所示，其中大谱线处理过程是以含干扰信号的FFT幅度与干扰门限之差作为判断干扰是否存在的依据作为多路开关的控制端。若在某频率处存在干扰则多路开关与下部的输入端，即将超出门限的谱线置零;否则多路开关接通上部的输入端，即将未超过门限的谱线值保留。从而实现了干扰的检测与存在干扰频率处的陷波处理。

图4 频域陷波抑制干扰与门限生成和谱线处理原理

2.2 仿真分析

根据FFT重叠变换干扰抑制算法原理，利用Simulink建立干扰抑制仿真模型，设定仿真条件如下:信源数码率为1 kb/s，扩频码(PN码)率为255 kb/s，载波为510 kHz，高斯白噪声信噪比为10 dB，存在 2个单音窄带干扰，信干比均为－30 dB，中心频率分别为510 kHz和1.5 MHz。仿真过程中，FFT变换的次数 M=1，FFT变换的长度NFFT=8192，衰减系数 η =0.3，1/4 重叠加窗处理的窗函数为第一旁瓣比主瓣低80 dB的切比雪夫窗。

干扰抑制前后的波形对比如图5所示。由图5可见，2个单音窄带干扰信号基本被滤除，但是干扰抑制后的波形相对于未被干扰的信号来说还有一定的起伏，这是因为干扰抑制算法无法抑制高斯白噪声的影响。但抑制后的信号完全可以通过后续的解扩解调还原出数据信号。

1/4重叠复用并经过频域陷波处理后各支路信号波形与4路对齐叠加后的信号波形如图6所示。由图6可见，经过4条支路干扰抑制后合并的信号，其数据段两端的衰减在对齐合并之后已经基本消失，即相对于单独一路加窗后的信号，数据段两端更加平滑，减小了加窗对有用信号的损伤。

干扰抑制前后信号的频谱如图7所示，可以看出，经干扰抑制后，高于干扰门限的谱线被衰减置零，而低于门限的谱线得以保留，从而在进行IFFT变换之后得到如图5所示的干扰抑制后的时域波形，进行下一步的解扩解调处理。

图5 干扰抑制前后的波形对比

图6 各支路经陷波处理后的波形及4路叠加波形

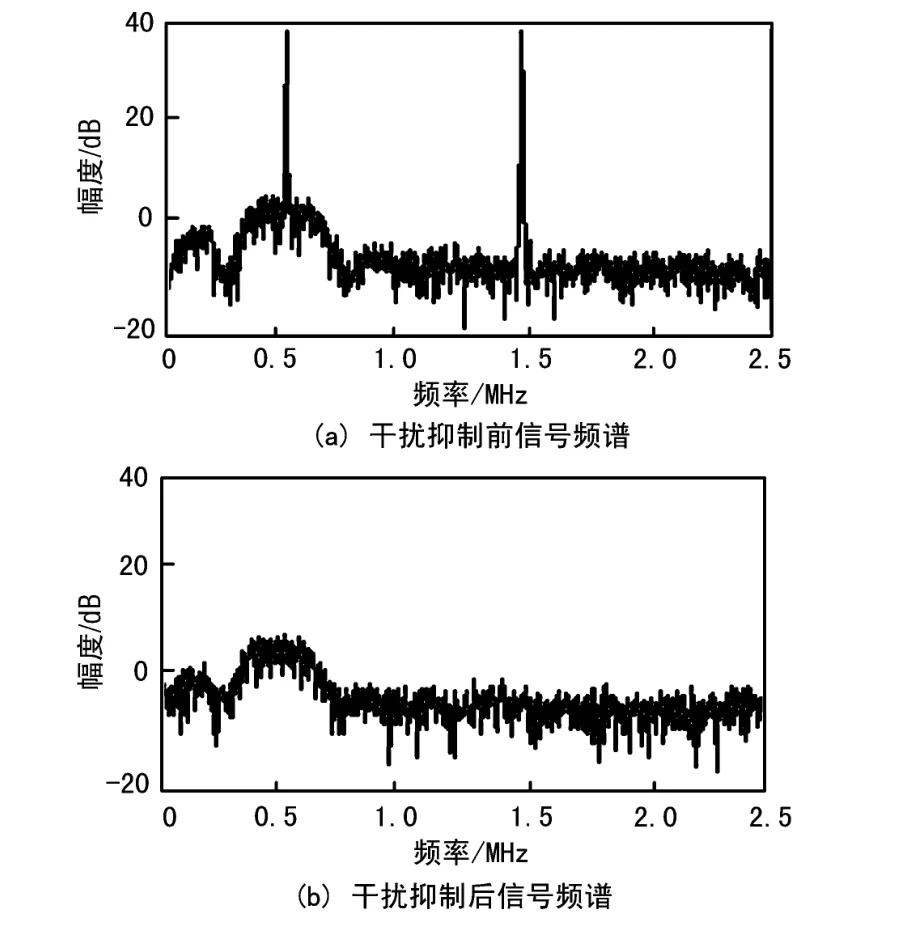
图7 窄带干扰抑制前后的信号频谱

通过以上仿真结果可知，在频域陷波处理时首先用低旁瓣的窗函数对时域信号加窗，并将各路加窗并经过陷波处理后的信号进行重叠处理，降低了窄带干扰的频谱泄露，从而使得干扰抑制后有用信号的损伤大为减少，这些措施共同促成了FFT重叠变换干扰抑制算法具有良好的窄带干扰抑制性能。

3 结束语

本文研究了FFT重叠变换干扰抑制算法的原理，利用Simulink构建模型进行了仿真分析，验证了基于FFT重叠变换的频域陷波技术抑制干扰的有效性，能够为直接序列扩频系统在干扰环境下的应用提供一定依据。通过仿真可知，该干扰抑制技术能够处理多个干扰，可用干扰的变化实现快速跟踪，并且窗函数和抑制算法选择合适，陷波深度可以非常大。 ■

［1］王 波.直接序列扩频通信系统中的窄带干扰抑制技术研究［D］.重庆大学，2009:17－18.

［2］赵 刚.扩频通信系统实用仿真技术［M］.北京:国防工业出版社，2009.

［3］陈 岩，赵 笃.直接序列扩频系统中的窄带干扰抑制［J］.计算机仿真，2006，23(10):100 －102.

［4］张贤达.现代信号处理［M］.北京:清华大学出版社，2003.

［5］CHEN Xiao-wen，GUO Wei，ZHENG Yong.Frequency Domain Interference Suppression in a DSSS System［J］.IEEE International Conference on Communications，Circuits and Systems and West Sino Expositions，2002，1(29):247－251.

［6］李 然，赵 刚.FFT重叠相加抗窄带干扰的算法研究［J］.四川理工学院学报(自然科学版)，2009，22(3):87－89.

［7］姚军勇，郑林华.频域抗干扰算法中的滤波门限问题研究［J］.现代电子技术，2007，24(1):1 －2.

［8］曾祥华，李峥嵘，王雪飞.扩频系统频域窄带干扰抑制算法加窗损耗研究［J］.电子与信息学报，2004，26(8):1276－1281.

［9］牛 海，郑剑云，朱义胜.基于Simulink的直扩通信仿真研究［J］.舰船电子对抗，2008，31(5):10 －12.

［10］张银蒲，孙茂松，窦桂华.基于FFT的扩频通信系统抗干扰技术研究［J］.唐山学院学报，2012，25(3):97－99.