基于原对偶内点法和分枝定界算法的配网无功优化计算及其并行实现

王 云，江全元

（浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

无功优化是指在满足各种约束条件下，利用无功控制手段，如控制可调变压器的分接头、可投切电容器投切数量等，来提高电压水平，降低系统有功损耗。但变压器变比和并联电容器组都不能进行连续的调节，因此，无功优化实质是一类非线性混合整数规划问题。如何有效地处理这些离散变量一直是该类问题的一个难点。多年来，国内外学者对此进行了大量的学术研究，并提出了一系列优化算法。

一种处理方法是先将离散变量作为连续变量参与优化，求得优化解后再进行简单的就近取整，但可能会导致某些约束越限。文献［1］提出了将无功优化问题中的离散变量进行二进制编码的连续化处理，从而把该混合整数优化问题转化为一个等价的连续优化问题来求解。文献［2-4］采用二次罚函数来处理离散变量，并将其嵌入到非线性原对偶内点法中。分枝定界法是一种求解混合整数规划问题的有效方法，学者们对此进行了大量的研究。文献［5］对分枝定界算法选择规则进行了较为深入的研究，提出一种快速分枝定界算法。文献［6］用常规的分枝定界法求解，计算量较大。文献［7］采用简化分枝定界法进行求解，计算量有所减少，但是不能保证获得最优解。文献［8］将原对偶内点法和分枝定界法结合起来求解最优潮流问题，实现了精确求解严格最优潮流问题，但是当离散量较多时，计算相当耗时。文献［9］运用原对偶内点法和分枝定界法解决电力系统无功优化问题，找到了比传统无功优化更加合理的全局最优解，针对大规模系统计算耗时，提出了简化分枝定界算法。并行分枝定界算法在整数规划问题中获得了大量的运用［10-12］：文献［10-11］深入研究了分枝定界并行策略，获得了良好的并行效果；文献［12］提出一种负荷平衡策略，获得较好的并行性能。

本文采用分枝定界法求解混合整数优化问题，采用原对偶内点法求解整数规划的松弛问题。由于完全分枝定界分枝数庞大，计算量大，本文提出一种并行分枝定界策略，采用主从机模式和异步通信策略，测试算例表明，该并行策略有效地提高了计算效率，各从机负荷平衡性好，获得良好的加速比。

1 配网无功优化数学模型

以系统有功损耗为目标函数，配电网络无功优化的非线性模型可表示成如下形式：

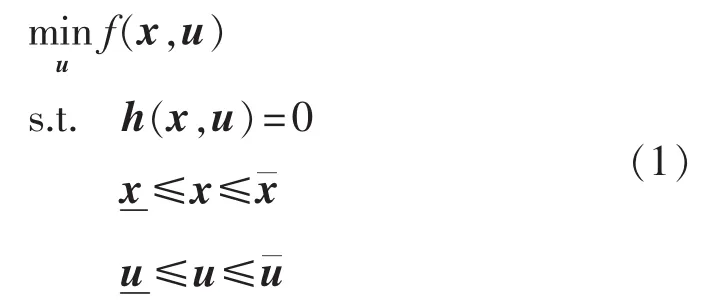
其中，f（x，u）为目标函数，表示配网有功损耗；h（x，u）=0表示配网潮流方程表示电压上下限约束，x是连续变量，由节点电压组成表示离散变量上下限约束，u表示离散变量，由可调变压器变比和无功补偿电容器投切组数构成。可见，这是一个混合整数规划问题。

1.1 目标函数值

以网络损耗最小为目标函数：

其中，Ploss（Q，T）表示电容器投切为 Q、变压器分接头档位为T时的网络损耗。

1.2 潮流方程约束

配网潮流方程约束采用电流不平衡形式：

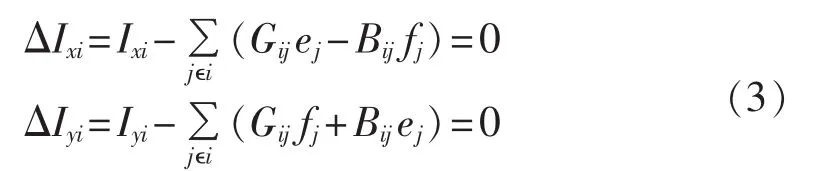
其中，PDi、QDi为节点 i有功和无功负荷；Gij、Bij为对应节点导纳；nB为节点数。

1.3 电压上下限约束

电压上下限约束表示为：

1.4 控制变量约束

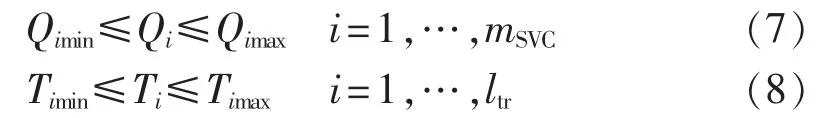
其中，Qi、Ti为离散变量，mSVC为装设电容器节点数；ltr为可调变压器台数。

2 原对偶内点法求解非线性规划问题

分枝定界法求解该混合整数规划问题时，需要求解大量的连续变量非线性规划问题，即不考虑离散变量约束的松弛问题，本文用原对偶内点法求解该非线性规划问题。原对偶内点法是现代内点算法中最好的算法，该方法鲁棒性强，收敛迅速。原对偶内点法求解非线性规划问题可参考文献［13］。

3 分枝定界法求解整数规划问题

分枝定界算法的基本思想就是对于可行解为有限数的有约束条件的最优化问题，把整个可行解空间反复地分割为越来越小的子集（称为分枝），并且为每个子集的目标函数值计算一个下界（称为定界）；在每次分枝后，凡是界限不优于已知可行解集目标函数值的子集不再进一步分枝（称为剪枝），这样许多子集可不予考虑。分枝定界算法具有以下4个基本定则。

a.分枝定则。

分枝定则定义如何将问题划分为子问题。一般选用二分法进行分枝，对未达到整数值的离散变量进行松驰，假如松驰子问题最优解中某一离散变量Xr的值不是整数，则构造Xr≤Ir和Xr≥Ir+1这2个约束分别加入原松驰子问题中形成2个新的子问题，Ir是Xr的整数部分。

b.定界定则。

定界定则定义如何计算一个子问题最优解的上下界。对已达到整数可行解的子问题最优解，判断其是否小于已知下界，若满足条件则进行修改。

c.选择定则。

选择定则定义应选择哪个子问题进行分枝。节点的选取方法就是考察一次分枝后，下一步应选择哪个或哪些节点继续进行分枝计算。主要有深度优先搜索和广度优先搜索。

d.削除定则。

削除定则定义如何识别和消去不可能产生原始问题的最优解的子问题，即识别和删除其中不良分枝。子问题无可行解、找到整数要求的可行解或者其目标函数值大于已知上界，则进行剪枝操作。

分枝定界算法求解混合整数规划问题基本步骤可概括如下［7］。

a.松驰原问题，即将离散变量连续化，并用原对偶内点法求解该非线性连续规划问题。若无解，则原问题无解；否则，置下界z为连续规划问题的目标函数值，置上界z为一足够大数。

b.若无可行解或解的目标函数值已超过z，转至步骤g；否则继续下一步。

c.若满足整数条件，转至步骤f；否则继续下一步。

d.分枝并记录分枝信息。选择父问题的最优解中某一非整数变量，构造Xr≤Ir和 Xr≥Ir+1这 2个新的约束，分别加入原松驰子问题中形成2个新的子问题。

e.选择其中一个分枝，用原对偶内点法求解，然后转至步骤b。

f.保存目前的最优解，并更新z。

g.若所有分枝都已检索完毕，则停止计算，至此得到的最优解就是原问题的最优解。

h.沿分枝回溯到最近一个尚未检索的分枝（后进先出），用原对偶内点法求解，然后转至步骤b。

由上可知，分枝定界算法在理论上可以找到最优解。实际计算中，当变量较少时，可以获得满意的结果，但当系统较大，尤其是整型变量较多时，分枝数较多，决策树庞大，需要占据较大内存，计算相当耗时，算法流程图如图1所示。

图1 分枝定界算法流程图Fig．1 Flowchart of branch&bound algorithm

4 并行分枝定界策略

为了应对串行分枝定界占用内存严重、计算耗时等问题，本文提出一种并行分枝定界策略，各工作机并行产生决策树，并行对各自的子问题执行分枝定界操作。分枝定界有多种并行策略，各并行策略与所使用的并行平台有很大关联。根据各机通信协议的不同可划分为同步和异步并行算法；根据工作内存数量的不同可划分为中央存储（共享内存）、分布式内存和混合存储策略。共享内存模式下，全部子问题保存在一个内存下；分布式内存下，各工作机保存各自的子问题并分别进行分枝定界搜索；混合存储，各工作机有各自的内存，同时有一个共享内存，供所有工作机共享。

本文使用分布式并行机平台、分布式内存存储策略。各并行机有各自的内存，存储各自的子问题并分别进行分枝定界搜索，各并行机采用异步通信模式。并行机控制采用主从模式，在并行机中选择一台作为主机，其余为工作从机。主机负责初始任务的产生和分配，协调从机工作进度，平衡各从机负荷，各工作从机对各自的子问题执行分枝定界操作。分枝定界并行算法需要解决的问题主要有：初始问题产生和任务分配，各工作从机负荷动态平衡，最优值上限交互，终止条件。

a.初始问题产生和任务分配。在算法执行起始阶段，只有一个子问题，因此，不可避免地存在一个并行起始阶段；另一方面，产生一些子问题就立刻启动并行未必是一个好策略，因为串行计算可能产生的最优值上下界会消除一些节点，从而导致并行时某些子树是无意义的计算。本文初始策略为：工作主机串行搜索根节点，直到产生K个子节点（子问题），K定义为工作从机的数量，然后把所得的K个子问题分配给各工作从机。

b.各工作从机负荷动态平衡。各工作从机负荷量一般以其子问题数量计量即可，工作从机负荷量发生变化都将其新的负荷量通知主机。主机负责任务的动态分配，平衡各工作从机负荷。当从机负荷量为零后，从机向主机请求分配任务，主机接到消息后，选择任务数最多的一个从机，请求其给该空闲机发送任务（N个），若从机发送N个任务后自身负荷量低于某设定值La，将通知发送任务失败。本文中，La、N均取为1。显然，该负荷平衡策略下，各工作机为异步通信模式，工作机间的通信可能发生在任何时刻。

c.最优值上下界交互。当某从机找到一个更好的最优值上界，其将该值广播给其他所有工作从机。

d.终止条件。在分布式内存消息模式下，终止条件一般设定为从机工作内存子问题都为空，并保证没有消息在机群间传送。

为了评价并行策略的有效性，提出如下并行分枝定界性能评价标准。

a.搜索树惩罚因子：定义并行子问题数与串行子问题数之比为搜索树惩罚因子Ps。

b.负荷平衡因子：各从机最小有效计算时间与最大有效计算时间之比为负荷平衡因子Lf。有效时间指的是进行分枝定界操作时间，不包括通信时间。

c.加速比：串行分枝定界计算时间与并行分枝定界计算时间之比为加速比S。

5 算例分析

5.1 测试算例

本文采用2个试验系统作为算例，对算法进行分析和验证，表1给出了2个测试算例的参数，其中，nL为系统线路数。试验系统1为23节点系统，有12台可调变压器，可调档位均为9档，有10个节点装设有可补偿电容器，电容器组数均为5组；试验系统2为25节点系统，有5台可调变压器，档位均为5档，5个节点装有可投切电容器，电容器组数均为6组。

表1 测试算例参数Tab.1 Parameters of tests

5.2 测试结果

根据上面提出的并行分枝定界策略，在19核和33核下测试以上2个算例，分析其性能，同时运用串行分枝定界算法对以上2个算例进行测试，分析其运行性能。工作主机硬件为2×Intel Xeon E5520 CPU，6×1 GB DDR3 1333 MHz内存，其他工作从机硬件为 2×Intel Xeon X5550 CPU，6×2 GB DDR3 1333 MHz内存。并行环境在MATLAB2009b环境下测试。所得结果如表2所示，表中M是并行起始阶段工作主机初始问题产生的个数；P是核的数目，包括1个工作主机和P-1个工作从机。运用串行分枝定界算法对这2个算例进行测试，分枝定界法用深度优先搜索策略，测试结果如表3所示。

表2 并行分枝定界算法性能分析Tab.2 Performance analysis of parallel branch&bound algorithm

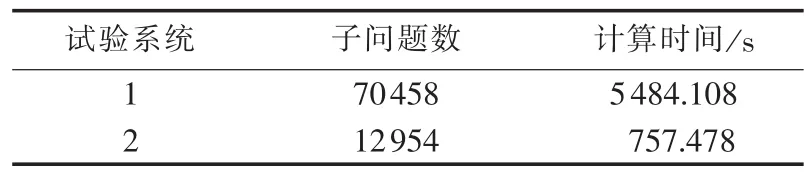
表3 串行分枝定界算法性能分析Tab.3 Performance analysis of series branch&bound algorithm

根据上面提出的并行分枝定界策略，并行起始阶段，工作主机串行产生P-1个子问题，并分配给P-1个工作从机，此后工作从机对各自的问题并行计算。从表2可以看出，2个试验系统的并行效果均较好，各从机负荷平衡性好，子问题数少于串行分枝定界算法问题数，获得良好的加速比，加速比甚至大于并行机数目，这是因为与串行分枝定界法相比，并行分枝定界算法可能提前找到更好的最优解从而避免了一些子问题的求解，由此减少计算时间，获得良好的加速比。此外，从表2可以看出，各工作从机平衡因子接近1，负荷平衡性好，因此，本文提出的负荷平衡策略是有效的。为了分析核的数量对该并行策略的影响，对25节点系统分别在3核、7核、13核、19核、25核和33核下进行测试。图2和图3分别描述加速比和负荷平衡因子随核的数量变化折线。从图2可以看出，该并行分枝定界算法几乎可获得超线性加速比，核的利用数量达33。异步通信模式下的并行算法，各工作从机负荷动态平衡是一个很重要的问题，从图3可看出，该并行分枝定界策略能适应不同核的数量，负荷平衡因子随核的数量增加有减少趋势，其值不低于0.955，负荷平衡性良好。

图2 加速比S变化折线Fig.2 Broken line graph of speedup ratio S

图3 负荷平衡因子Lf变化折线Fig.3 Broken line graph of load balancing factor Lf

6 结论

无功优化是一类非线性混合整数规划问题，对于离散变量的处理一直是该问题的难点。本文提出一种并行分枝定界算法，各工作从机并行产生决策树，分别进行分枝定界操作，主机负责初始任务产生和分配、各工作从机任务动态分配和负荷平衡等。测试结果表明，该并行分枝定界策略运行效果良好，搜索树惩罚因子低，负荷平衡因子接近1，获得良好的加速比。本文算法有如下特色：

a.本文中各并行机通信采用异步通信模式，各从机通信可能发生在任何时间，与同步通信模式相比，可有效地降低等待时间；

b.本文并行策略中分配一台计算机为主机，负责初始任务分配和负荷动态平衡，测试算例表明，本文提出的分枝定界算法负荷平衡性好，可获得良好的加速比；

c.与串行分枝定界算法相比，本文提出的并行分枝定界策略产生的子问题数有所减少，甚至可获得超线性加速比，这是因为并行分枝定界算法可能提前找到一个更好的最优解从而避免一些子问题的计算；

d.本文提出的分枝定界并行策略采用异步通信模式，异步通信模式下的并行算法需要解决各并行机负荷平衡问题，测试算例表明，本文提出的并行分枝定界策略负荷平衡性良好，能适应不同数量的并行机。