分布式发电微网系统暂态时域仿真方法研究
——(一)基本框架与仿真算法
2013-10-17王成山黄碧斌丁承第
李 鹏 ,王成山 ,黄碧斌 ,高 菲 ,丁承第 ,于 浩
(1.天津大学 智能电网教育部重点实验室,天津 300072;2.国家电网能源研究院,北京 100052;3.中国电力科学研究院,北京 100192)
0 引言
电力作为重要的二次能源,传统的集中式电能生产方式受到挑战,分布式发电技术[1-2]的蓬勃发展正推动着电力工业经历几十年来最为深刻而持久的变革,并被认为是代表了未来电力工业的发展方向。
分布式发电技术的成熟与发展使得电能生产价格不断下降,为分布式发电技术的规模化应用提供了可能。现有研究和实践表明,将分布式发电系统以微网的形式接入到大电网并网运行是发挥其效能的最有效方式[3]。大量分布式电源的并网运行必将对微网及所接入的配电系统的运行特性、电能质量、电压与频率调节以及继电保护等方面产生诸多影响,定量分析这些影响对微网及整个电力系统的规划、设计、运行与科学研究具有十分重要的意义[3]。
与传统的电力系统相比,分布式发电微网系统有其自身特点,主要体现在:
a.分布式电源种类繁多且形式各异,既有静止的直流型电源,也有旋转的交流电机;
b.大部分类型的分布式电源需通过电力电子变流器向电网或负荷供电;
c.通常具有并网和独立运行等多种模式;
d.许多分布式电源的出力具有间歇性和随机性,往往需要储能设备、功率补偿装置以及其他种类分布式电源的配合才能达到较好的动、静态性能;
e.分布式发电微网系统控制复杂,它包括分布式电源及储能元件自身的控制、电力电子变流器的控制以及网络层面的电压与频率调节;
f.有的分布式电源在运行时不仅要考虑系统中电负荷的需求,有时还要受冷、热负荷的约束,达到“以热定电”或“以冷定电”的目的;
g.中小容量的分布式电源大多接入中低压配网,此时网络参数与负荷的不对称性大幅增加,此外,用户侧的分布式电源可能采用单相逆变器形式并网,更加剧了系统的不对称性。
因此,系统的运行状态会随着外部条件的变化、负荷需求的增减、电源出力的调整、运行方式的改变以及故障或扰动的发生而不断变化,其动态过程也将更为复杂。此时,仅依靠稳态分析的方法是不够的,必须借助有效的暂态仿真工具以获取分布式发电微网系统在各种复杂运行情况下的时域响应特性。
对传统电力系统的分析研究通常借助于数字仿真和动态模拟来实现[4],而分布式发电微网系统的相关研究不但可以借助真实的物理装置,一些情况下实验系统甚至可以按1∶1的比例真实地再现研究对象[5]。尽管如此,相对于物理试验,数字仿真在经济性和灵活性等方面仍保持着独特的优势,具有不可替代的作用。传统电力系统数字仿真的研究分别针对电磁暂态过程与机电暂态过程发展出了相应的数字仿真方法,即电磁暂态仿真方法与机电暂态仿真方法[6]。分布式发电微网系统的数字仿真方法研究可借鉴传统电力系统数字仿真的经验,即以电磁暂态仿真方法为基础研究分布式发电微网系统中相对较快的动态过程,而以机电暂态仿真方法为基础研究其中相对较慢的动态过程,其中“较快”和“较慢”在一般情况下以工频为界加以区别是合适的。
分布式发电微网系统稳定性仿真侧重于分布式发电微网系统中各种变化较慢的暂态过程的仿真,通过采用简化模型对系统进行建模,适当忽略了系统中快动态过程的影响,基于电力系统机电暂态仿真的基本理论与方法,具有相对较快的仿真计算速度,适于高渗透率下大规模微网系统的仿真计算,主要用于分布式发电微网系统的稳定性分析及仿真、控制器策略验证等方面的研究。
分布式发电微网系统暂态仿真侧重于分布式发电微网系统中各种快速变化的暂态过程的详细仿真,在系统层面进行详细建模,采用电力系统电磁暂态仿真与电路仿真的基本理论与方法,可捕捉频率从几百kHz到工频之间的动态过程。从应用对象上看,分布式发电微网系统暂态仿真主要用于分布式发电及微网系统的规划、设计、运行以及科学研究等方面;从功能上看,分布式发电微网系统暂态仿真主要用于分布式发电微网系统稳态时的谐波分析、电压与频率控制、能量管理,暂态时的短路电流计算、故障穿越特性、紧急控制、保护装置整定以及实际物理系统的试验与验证等诸多方面。
本文着重关心分布式发电微网系统中快动态过程数字仿真的相关问题,即文中所提到的“暂态仿真”,详细介绍了分布式发电微网系统暂态仿真的基本问题与挑战,提出了基于节点分析法实现的分布式发电微网暂态仿真的基本框架,从建模需求、算法可行性、设计与实现难度、可扩展性及工程应用等多个角度比较了当前各种算法的优劣,解决了分布式发电微网系统暂态仿真的基本问题,为今后开发更加高效的暂态仿真算法奠定了基础。
1 暂态仿真的基本问题
1.1 问题与挑战
按分布式电源类型的不同,典型的分布式发电系统包括燃料电池发电系统、光伏发电系统、微型燃气轮机发电系统、风力发电系统等,典型的储能装置包括蓄电池储能、飞轮储能以及超级电容器储能等。利用分布式电源及储能元件动态特性的差异可组成各种混合发电系统,如风光蓄发电系统等。微网是指由分布式电源、储能元件、能量转换装置、相关负荷和监控、保护装置汇集而成的小型发配电系统,是一个能够实现自我控制、保护和管理的自治系统,其核心在于能够实现并网与独立运行2种模式及模式间的切换[7]。本文立足于从方法上解决分布式发电微网系统暂态仿真时的各种建模与仿真算法问题,其核心在于各种分布式电源、电力电子装置及控制器模型的建模与求解。
分布式发电微网系统可以有多种能源输入、多种产品输出、多种能量转换单元、多种运行与控制方式,其动态过程可能包括了化学反应过程、热力学动态、机械传动过程以及电磁场间的作用,分布式发电微网系统自身各动态过程间的相互耦合与相互作用决定了它将是一个十分复杂的非线性动力学系统,并且在并网运行时,分布式发电微网系统的动态特性将“传导”到其所接入的配电网络中,从而改变整个配电系统的动态特性。
分布式发电微网系统自身的特点对分布式发电微网暂态仿真提出了新的挑战,包括以下几个方面:
a.丰富的分布式电源类型和不断丰富、发展的分布式电源模型需要数字仿真程序具有强大的建模能力;
b.分布式电源本身及其控制器模型都具有较强的非线性,整个分布式发电微网系统是一个强非线性系统;
c.在需要精确计及电力电子装置动态特性的场合,采用开关模型的电力电子器件的频繁动作对程序的计算精度和数值稳定性提出了较高要求;
d.当微网系统规模较大,电气网络复杂,同时含有多个分布式电源时,程序的计算负担也是必须着重考虑的问题;
e.需要基于开放的设计架构以面向今后的扩展以及同其他仿真程序的交互、融合。
1.2 理论基础
在分布式发电微网系统的动态过程中,一般而言电场与磁场间的相互作用变化较快,相比之下热力学等动态过程的变化则较为迟缓,它们在运行时,特别是在暂态过程中,将体现出完全不同的时间尺度特性。与传统的电力系统暂态过程划分不同,分布式发电微网系统暂态过程的时间尺度可能还需要进一步研究,因此采用尽可能详尽的系统级元件模型以得到系统运行时详细、充分、完整的动态响应特性是至关重要的;另一方面,由于大部分分布式电源惯性较小,暂态过程中特别是独立运行的分布式发电微网系统的频率通常会随着故障的发生及负荷的突变剧烈波动,此时可利用详细的暂态仿真结果作为分布式发电微网系统模型简化与仿真方法验证的依据。此外,对分布式发电微网系统中快动态问题的研究,如系统的故障穿越能力[8]、谐波与电压闪变、防孤岛保护、铁磁谐振、次同步谐振[9]以及用于二次设备设计[10-11]和测试的实时仿真[12]等,需要得到系统中各种参数(主要是电气量)随时间变化的“真实的”响应曲线,以瞬时值描述的系统响应特性曲线也同样需要系统级的详细建模。从仿真方法看,通过对元件的详细建模以捕捉具有快动态特性的暂态过程并得到详细、充分、完整的系统动态响应特性属于电力系统电磁暂态仿真的范畴。
1.3 基本框架
从仿真方法上看,电力系统电磁暂态时域仿真的基本框架可以分为基于状态变量分析法和基于节点分析法 2 类[13]。前者以 MATLAB/SimPowerSystems为代表,属一般性的建模方法,不仅能仿真电力系统的各种动态过程,同时也能求解以微分方程描述的动力学系统的其他问题,方法更具普遍性和一般性;后者则以EMTP-RV、EMTDC和ATP等为代表,统称为EMTP类程序。状态变量分析法的基本步骤之一是形成式(1)形式的状态变量方程:

具有标准形式的状态方程可使用各种成熟的数值计算程序进行求解,但与式(2)的节点方程相比,状态方程的形成要复杂和困难得多。通常情况下,以微分方程描述的元件特性方程并不能直接形成式(2)形式的节点方程,而是需要先应用具体的数值积分算法对元件的特性方程进行差分化得到诺顿形式的等效电路,通过联立元件的差分方程得到式(3)形式的节点电导方程进行求解。对图1(a)所示电路应用数值积分算法后得到的等效计算电路模型如图1(b)所示。这里的数值积分算法包括梯形法、后向欧拉法等各种隐式算法,梯形法由于良好的数值稳定性、简单的形式以及较高的计算精度成为首选的方法。状态变量分析法与节点分析法的根本区别在于式(1)不含有任何数值算法,而式(3)则已是由微分方程差分化后得到的代数方程组,因此从计算求解的数值方法上状态变量分析法显得更加灵活,但计算过程也更加费时,此外,它在处理开关拓扑、某些非线性元件、频率相关元件及系统元件初始化时也不如节点法方便[13];而节点方程与定步长梯形法则构成了EMTP类程序的基本框架,它具有良好的数值稳定性和较快的计算速度,适用于大规模系统的计算求解,并被当前包括实时仿真工具在内的许多专门的电力系统电磁暂态仿真工具所采用。考虑到实现难度、算法的数值稳定性和计算速度,本文将基于EMTP类程序的基本框架实现分布式发电微网系统的暂态时域仿真。

图1 电路示例及等效计算电路模型Fig.1 Circuit example and its equivalent circuit model
对EMTP类程序而言,其中的电气系统与控制系统是分别求解的[14-15],如图2所示,这主要是考虑到电气系统中绝大多数元件是线性的,仅含少量的非线性元件(如电机、非线性阻抗等),可通过补偿法或预测校正法等方法与节点方程接口;而对控制系统而言,其特性主要以元件的输入/输出关系来描述,这与电气系统有较大不同,同时在控制系统中也含有较多的非线性环节,如非线性代数运算、限幅环节等。因此,按照元件的物理属性分别在电气系统与控制系统中建模并分别求解是合适的,此时电气系统与控制系统之间将存在一个步长的时延。这里采用同样的方法对元件进行建模求解。
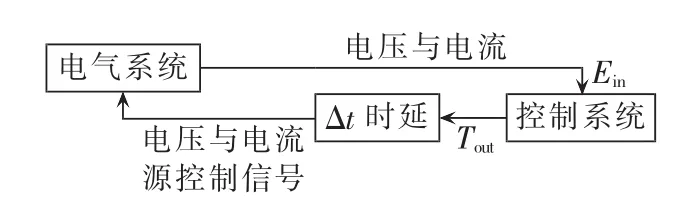
图2 电气系统与控制系统求解示意图Fig.2 Schematic diagram of solution calculation for control system and electrical system
2 系统建模与解算方法
2.1 增广的改进节点方程
电气系统的求解主要是基于式(2)的节点方程通过差分化后的元件伏安关系形成式(3)形式的节点电导矩阵。但受节点方程的限制,式(2)不能很好地处理受控源支路(如理想变压器模型)及不接地的理想电压源等模型。为此,SPICE采用改进的节点方程 MNA(Modified Nodal Approach)[13]以提高程序的建模能力,在此基础上文献[16]提出了增广的改进节点方程,如式(4)所示。与改进的节点方程相比,式(4)中增加了理想开关支路的元件特性,当开关关断时满足is=0,而开关闭合后支路两端电压满足ui-uj=0的关系。本文亦采用式(4)对分布式发电微网系统的电气网络进行建模。

式(4)可用于计算系统的稳态解、时域仿真及频率扫描。以图1(a)所示的简单电路为例,采用理想开关模型建模且开关闭合后,暂态仿真时形成的增广的改进节点方程如式(5)所示。

在对电力电子器件进行建模时,本文采用基于双电阻表示的开关模型而非理想开关模型[14],这主要是考虑到开关状态改变时算法的稳定性。此时,增广的开关支路可用于支路电流的测量。当网络的拓扑结构改变时,如开关关断或闭合、非线性元件状态改变等,需重新形成电导矩阵,通过节点编号可仅对受拓扑结构变化影响的部分进行局部重新因子分解以提高计算速度[17],但这需要稀疏求解算法的配合。
2.2 基于牛顿法的控制系统求解
控制系统仿真最初是为了实现HVDC变流器的控制器建模,并通过子程序TACS(Transient Analysis of Control Systems)提供给 EMTP 的[14]。控制系统的基本元件包括了各阶传递函数、典型的非线性环节及各种基本的代数运算、比较运算、逻辑运算环节等;与电气系统不同,控制系统的元件特性主要以输入/输出关系来描述,通过各种基本环节的组合与拓扑连接从而实现复杂的动态、静态及非线性特性;相对于电气系统,控制系统的建模能力更强,不仅可用于对发电机的原动机、励磁调节器以及各种控制与保护装置等在内的二次设备进行建模,还可以对具有复杂非线性特征的电气元件进行建模,在分布式发电微网系统暂态仿真建模中具有十分重要的作用。式(6)给出了微型燃气轮机发电系统暂态仿真中常用的永磁同步电机模型[18-19]。

其中,p为电机极对数,ωr为转子的机械角速度,λ为永磁通,J为电机的转动惯量,D为阻尼系数。
图3以传递函数的形式对该模型加以描述,它可通过控制系统的基本元件实现建模,其中函数f=Te=1.5p[λiq+(Ld-Lq)idiq]。
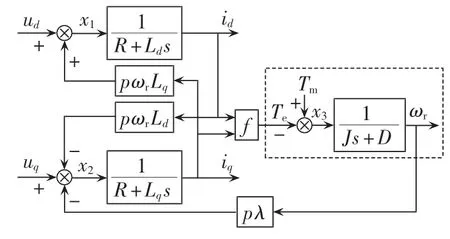
图3 以传递函数描述的永磁同步电机模型Fig.3 PMSM model expressed by transfer functions
控制系统通过联立求解各基本环节的元件特性得到系统输出的暂态时域解,与电气系统相似,对以传递函数表示的动态环节需要首先应用数值积分方法差分化后得到描述输入/输出关系的代数方程[14,20],这里同样以梯形法作为首选的数值算法。对图3中的3个一阶传递函数差分化后可得到式(7)的关系;以图3中虚线所表示的线性部分为例,联立后的系统方程可表示为式(8),此时认为Tm=um及Te=ue为系统输入。相对于电气系统,控制系统元件的非线性特征更强,种类也更丰富。早期的EMTP程序通过对非线性元件特性插入一个步长的时延可以将非线性问题化为线性方程组求解[14],这称为伪非线性方法。文献[15]通过联立控制系统的线性及非线性方程形成了式(9)形式的牛顿法迭代格式,消除了伪非线性方法产生的控制系统内部时延,改善了解的精度和数值稳定性。若整个系统都是线性的,则雅可比矩阵J为常数,每个仿真步长下只需一次线性方程组的求解即可得到系统的暂态解;若系统中存在非线性元件则需要进行迭代。实际应用时,可不必在每次迭代中都重新形成雅可比矩阵,通过迭代次数控制雅可比矩阵的更新可在一定程度上提高控制系统的解算速度,这称为伪牛顿法(pseudo Newton method)。
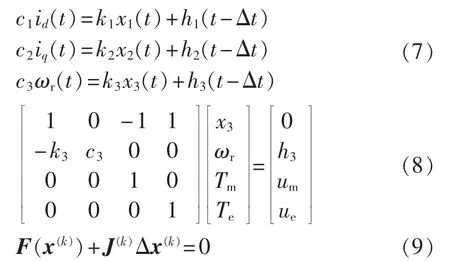
2.3 电气系统求解的插值算法
当前,各种形式电力电子变流器在分布式发电微网系统中获得了广泛的应用,它被用于不同频率、不同电压及交直流系统间的电能转换。对系统级仿真研究而言,主要强调电力电子装置对系统整体的影响而不必过多地考虑开关本身的非线性特性,采用简化的开关模型是合适的[21]。如前所述,基于节点分析框架的暂态仿真算法采用定步长的梯形法,使得开关状态的改变只能在步长的整数倍时刻,这不但会导致电压、电流波形出现不真实的“尖峰”(即非特征谐波),同时在开关动作后梯形法也会引起数值振荡;此外,电力电子装置中的大量开关模型会在仿真的某一时刻出现由于一个开关动作而引起的连锁反应情况,即同步开关动作[22];对于定步长算法,由于电力电子装置的频繁动作,在一个仿真步长内可能会出现多个开关动作时刻,这被称为多重开关[23]。综上所述,对采用节点分析框架的暂态仿真方法需要解决定步长引起的开关动作与仿真步长不一致及多重开关问题,需要解决同步开关的动作问题,需要解决开关动作后梯形法引起的数值振荡问题。
文献[24-25]提出的临界阻尼调整(CDA)技术通过在开关动作时刻改用2个半步长的后向欧拉法可解决数值振荡问题,在此基础上文献[26-27]提出的“同步响应法”(SRP)改进了CDA技术,以解决电力电子装置中的同步开关动作问题。当前,基于线性插值的方法解决电力电子电路的仿真问题获得了较多的关注[28-31],并被 EMTDC 等离线仿真工具所采用[17]。其中,文献[29]改进了文献[28]中的插值算法仅适用于自然换向的情况,同时由于数值振荡是围绕“真值”上下的等幅振荡,通过再次插值得到开关动作后梯形法步长的中点值消除了数值振荡。该算法在仿真过程中仅采用梯形法一种数值积分方法与插值算法相配合,较易于实现,但它认为插值得到开关动作时刻动作前的节点注入电流源列向量i-(即式(3)中的i)和开关动作后的i+是相同的,这可能会影响仿真结果的计算精度。文献[30]在NETOMAC算法的基础上通过外插和后向欧拉法的配合得到了开关动作时刻开关动作后新的网络拓扑结构和系统初值,实现了“重初始化”。文献[31]在文献[30]的基础上考虑了同步开关检测过程中出现的多重开关动作,将系统重初始化时刻选在开关动作后的半个步长点上,算法的基本步骤见图4[27],这里简单介绍如下:
a.由t-ΔT时刻使用梯形法积分一个步长至t;
b.由t时刻使用梯形法积分一个步长至t+ΔT,此时检测到td时刻的开关动作;
c.由t和t+ΔT时刻值内插到td时刻值;
d.改变开关状态,重新形成暂态计算矩阵,以后向欧拉法积分半步长至td+ΔT/2,并检测该时刻各开关动作条件,如果没有开关动作则转入下一步,否则重复步骤d;
e.由 td和td+ΔT/2外插到td-ΔT/2时刻值;
f.在td-ΔT/2时刻以后向欧拉法积分至td;
g.在td时刻以后向欧拉法积分至td+ΔT/2;
h.在td+ΔT/2时刻以梯形法积分至td+3ΔT/2,此时需重新检测开关状态。

图4 电气系统插值方案Fig.4 Interpolation scheme applied in electrical system
本文采用上述的插值方案作为处理电气系统中电力电子开关的解算方法。线性插值算法简单、方便、有效,它假设在相邻的2次开关动作之间的系统特性可以用线性关系拟合,总体而言它对系统计算负担增加不大。由于控制系统中存在较多的非线性环节(包括连续的和离散的),并通过迭代计算求解,此时线性假设不成立,且算法实现也较为困难,因此本文对控制系统的解算不进行插值,这会导致强制换向元件的控制信号的时延,但它已被包含到电气系统与控制系统解算本身的时延之内。实际应用上述插值算法时,需要将仿真结果与控制系统在仿真的整步长时刻同步,在完成步骤g的后向欧拉法积分后,需要根据td+ΔT/2与t+ΔT的相对位置决定是先同步到t+ΔT时刻再进行步骤h的梯形积分,还是先进行步骤h再进行同步。
3 初始化
暂态仿真的启动需要一个合理的初始运行点,合理的意思是指满足该时刻系统中的所有代数约束,否则可能会引起仿真结果的数值振荡等问题,对于电气系统而言主要的代数约束包括KVL和KCL等。当前,包括稳态解(steady-state solution)初始化、潮流解(power flow solution)初始化及零状态初始化在内的3种初始化方法在电磁暂态仿真中均得到了应用,如EMTP就提供了不同的初始化方法。基于稳态解的初始化方法对于简单的小规模系统是合适的,但对于大规模电力系统可能采用潮流解初始化的方法更有效[32],在参数不对称、负荷不平衡的配电系统中可能还需要多相潮流算法的支持[33]。在分布式发电微网系统中,交直流母线处的谐波成分很高,要实现含有各种电机模型及大量开关元件的电气系统的初始化是非常困难的,同时要保证控制系统中的大量非线性元件在同一时刻也被正确初始化就更加困难[13]。分布式发电微网系统暂态仿真的初始化问题本身就是一个值得研究的科学问题。因此,这里采用零状态初始化方法用于本文的研究工作,它同样也被EMTDC等仿真工具所采用。
4 结语
分布式发电微网技术的广泛应用需要特别重视各种分布式电源接入系统后的影响。分布式电源种类的多样性、一次能源的随机性、控制系统的复杂性决定了分布式发电微网系统的动态过程相对于传统配电系统将更复杂,同时分布式发电微网系统也更接近终端用户,担负着提供安全、可靠、清洁、经济的能源供给的任务。对分布式发电微网系统快动态过程的分析、研究需要详细的时域仿真结果,本文采用基于节点方程的电磁暂态仿真的基本框架作为分布式发电微网系统暂态仿真的基础,介绍了实现暂态仿真所采用的各种算法,具体包括采用增广的改进节点方程扩展了电气系统的建模能力;采用牛顿法迭代求解控制系统消除了非线性元件的内部时延;利用伪牛顿法提高了控制系统计算速度;采用插值算法解决电力电子开关仿真时的同步开关及数值振荡等问题。通过比较,分析了不同算法的优劣。最后,本文讨论了分布式发电微网系统初始化的各种方法,认为采用零状态初始化是当前可行的方法。
