水火弯板机系统中三维重建技术的研究

钟 华，程良伦

ZHONG Hua，CHENG Liang-lun

（广东工业大学 自动化学院，广州 510006）

0 引言

在目前的水火弯板机系统中，主要是利用激光测距仪对钢板加工数据进行测量，其主要问题如下：须有操作人员的干预，不能实现全自动化的生产。对一块10米长3米宽的钢板，测量时间长达十分钟左右。为了解决这个问题，本论文拟采用基于机器视觉的三位重建方法对钢板进行三维重建，系统直接从三维重建后得到的立体图形中取得生产所需的尺寸数据。

1 研究背景

文献[1]提出了利用编码结构光的方法对头像进行三位重建，重建的精度高，速度快。

文献[2]提出针对文献[1]存在的编码结构光易受到环境影响，对编码结构光的方式进行了改进。

文献[3]指出了相移的缺点，并提出线移的概念。投影图案由等宽的条纹组成。通过寻找这些相移图案的边缘来增加测量点密度。

文献[4]针对图像的特征点匹配问题，提出了一种基于小波多分辨率特征的字符串匹配算法。

文献[5]针对研究并实现了一种基于多特征约束的分阶段立体匹配算法。

针对广船项目三维重建的特点，本论文提出基于图像特征点的三维重建方法，以解决目前三维重建方法中存在的点云数量庞大，设备精密不适用于工业现场的问题。

2 研究内容

基于特征点的三维重建主要包括，照相机标定、特征点坐标提取和特征点匹配三个部分构成。

2.1 照相机标定

照相机的标定是为确立图像中的某一点u(u0,v0)与其空间点U(X0,Y0,Z0)之间的对应关系，这个对应关系可由一个3×4的矩阵来表示。

通过引入摄像机坐标系，照相机坐标系和世界坐标系等辅助坐标系，推导出得到世界坐标系中P（Xw,Yw,Zw）点和其在图像坐标系中的p(u,v)点之间的对应关系为[6]：

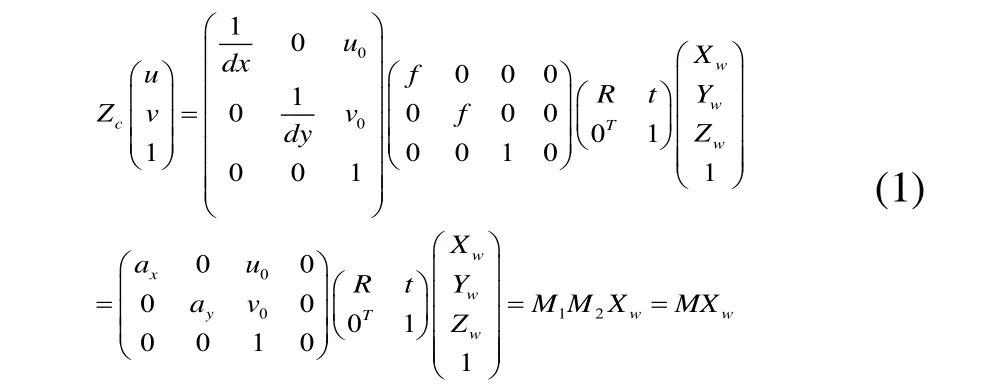
其中M1为照相机内参数矩阵，M2为照相机外参数矩阵。确定M1，M2矩阵参数的过程称为照相机的标定。

本文利用camera calibration tools这个标定工具[7]进行标定。

2.2 特征点图像坐标系的求取

在广船项目中，由于三维重建的目标物体为大面积的钢板，表面平整，先用Led点阵向钢板投影，双目照相机对钢板拍照如图1左图所示，通过图像处理，可以得到质量较好的右图像。

视光点为正方形，寻找特征点的工作简化为寻找图像中白色方块的中心坐标。其处理过程为：

图1 处理前后的Led点阵图像对比

1）特征点的个数是不定的，需要用一个单向链表来保存白色方块的首个像素的坐标，每次检测到一个新的白色方块，就将此白色方块的首像素的坐标插入链表的尾部，直到程序检测到所有的白色方块位置。此链表称为集团链表。

2）由于白色方块的大小未定，即每个方块中包含多少白色像素点不能确定，所以以集团链表的每个节点为起始点，创建一个新的链表，此链表称为子集团链表，每当检测到某个白色像素点属于某个集团，就将此白色像素点纳入该集团内。

对每个集团链表的特征点都采用此方法进行聚类，完成整个数据结构的建立。

完成整体数据结构的创建以后，遍历每一个子集团链表，得出其第一个结点图像坐标数据(x0,y0)和最后一个结点图像坐标数据(xn,yn)的数据，则此白色方块的中心坐标(xc,yc)可有下列的公式得到：

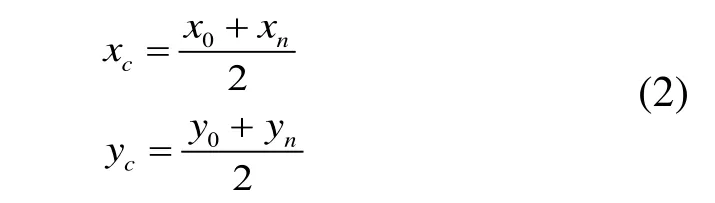
数据结构如图2所示。

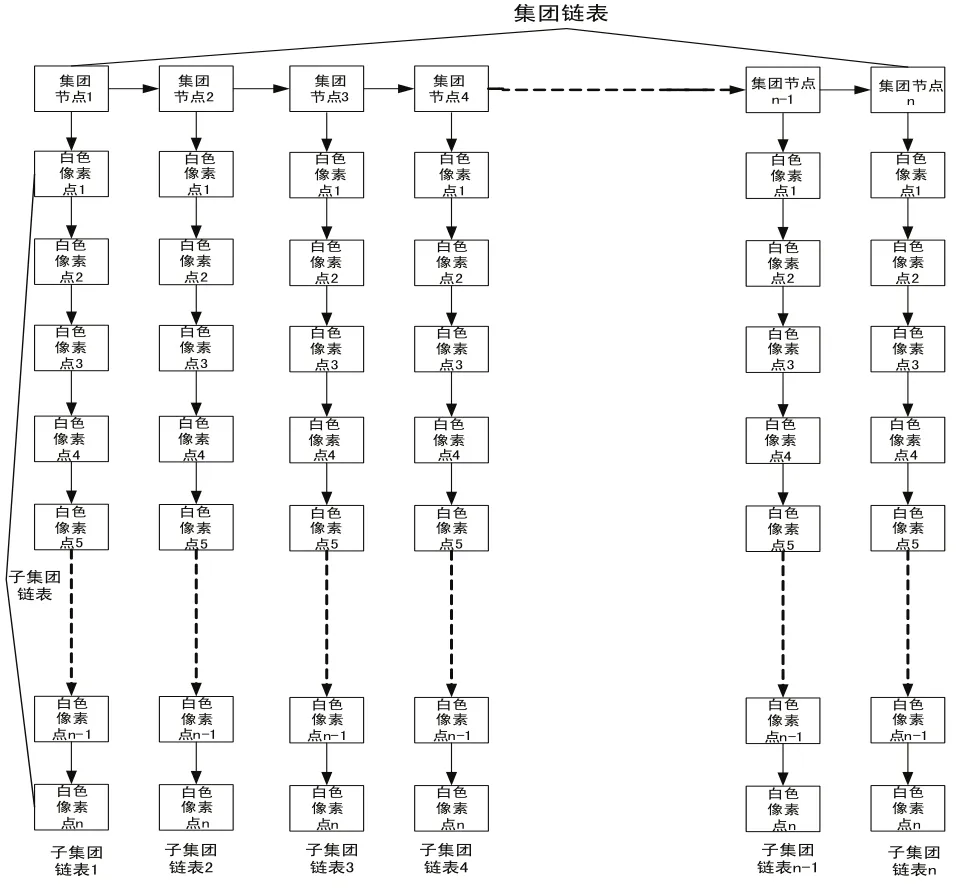
图2 数据结构形成示意图

2.3 特征点匹配

在三维重建中，实现特征点匹配是一个关键问题。

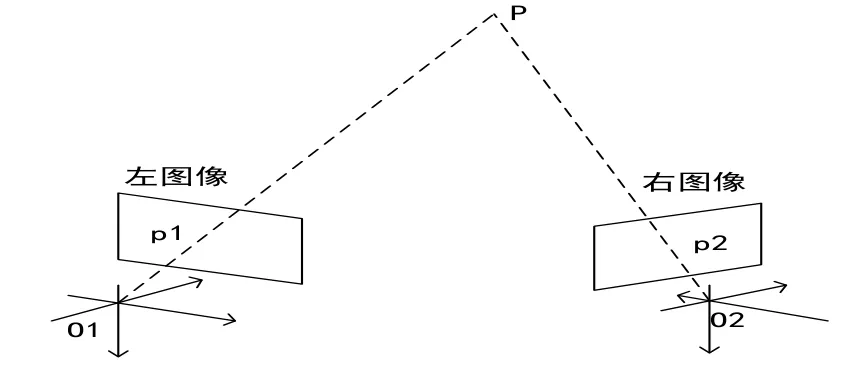
图3 双目照相机示意图

对于两图像的集团链表来说，其特征点是相对应的。也就是说按照从上到下，从左到右的顺序，左右图像特征点是相互对应的。对左右两幅钢板图像进行特征点聚类操作，完成特征点的匹配工作。其结构如图4所示。

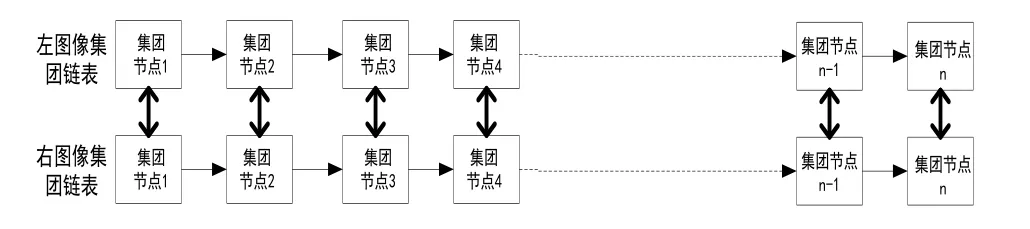
图4 特征点匹配示意图

在图4中，两个集团链表节点之间的双向箭头表示这两个节点所在的特征方块的中心坐标点是一对特征点对。

2.4 多个空间点的重建

在图3中，左图像中的某一点p1，其对应为空间直线Pp1，若要得到P点，则需要另外一台照相机在另外一个角度对P点进行拍照，得到右图像，在有图像中p2点对应的空间直线Pp2，Pp1和Pp2相交于唯一的空间点P，p1和p2称为特征点对。设其投影矩阵分别为M1，M2，得到下列方程组：

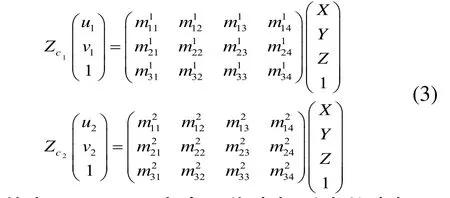
其中(u1,v1)是p1点在图像坐标系中的坐标，(u2,v2)是p2点在图像坐标系中的坐标。(X,Y,Z)是P点在世界坐标系中的坐标。解这个方程组，就可以求出P点在空间坐标系中的坐标。

本论文中的试验用到了34个点，实验过程如下。

3 试验数据

对实验室中任取的一个弧面进行了重建，弧面如图5左图所示。

弧面的重建用到了20个特征点，均匀的分布在如图5左图的170mm×100mm弧面上，以下为数据：

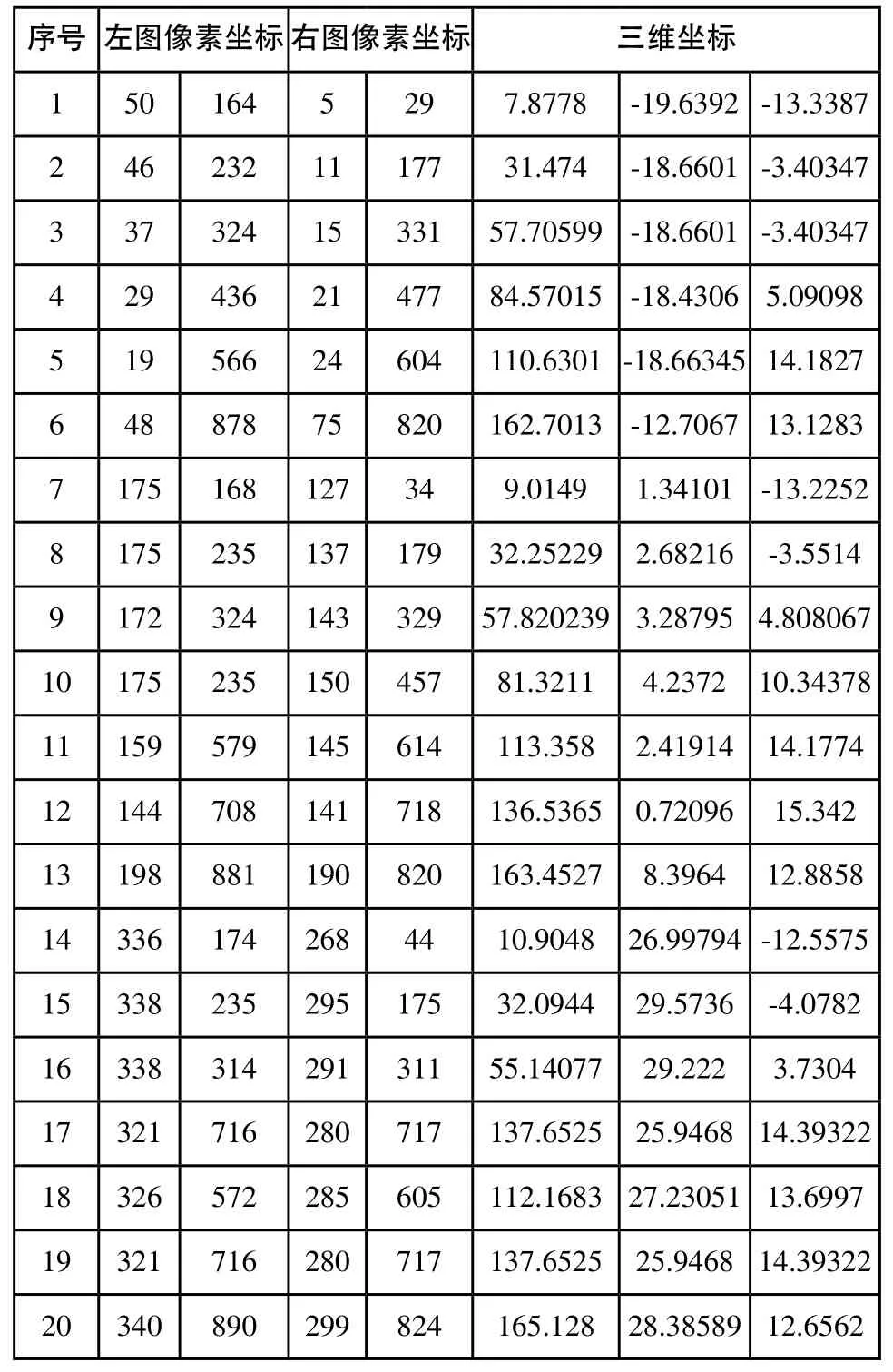
序号 左图像素坐标右图像素坐标 三维坐标1 50 164 5 29 7.8778 -19.6392-13.3387 2 46 232 11 177 31.474 -18.6601-3.40347 3 37 324 15 331 57.70599 -18.6601-3.40347 4 29 436 21 477 84.57015 -18.4306 5.09098 5 19 566 24 604 110.6301-18.66345 14.1827 6 48 878 75 820 162.7013 -12.7067 13.1283 7 175 168 127 34 9.0149 1.34101 -13.2252 8 175 235 137 179 32.25229 2.68216 -3.5514 9 172 324 143 329 57.820239 3.28795 4.808067 10 175 235 150 457 81.3211 4.2372 10.34378 11 159 579 145 614 113.358 2.41914 14.1774 12 144 708 141 718 136.5365 0.72096 15.342 13 198 881 190 820 163.4527 8.3964 12.8858 14 336 174 268 44 10.9048 26.99794-12.5575 15 338 235 295 175 32.0944 29.5736 -4.0782 16 338 314 291 311 55.14077 29.222 3.7304 17 321 716 280 717 137.6525 25.9468 14.39322 18 326 572 285 605 112.1683 27.23051 13.6997 19 321 716 280 717 137.6525 25.9468 14.39322 20 340 890 299 824 165.128 28.38589 12.6562

实际弧面和Matlab重建的弧面图形如图5所示。

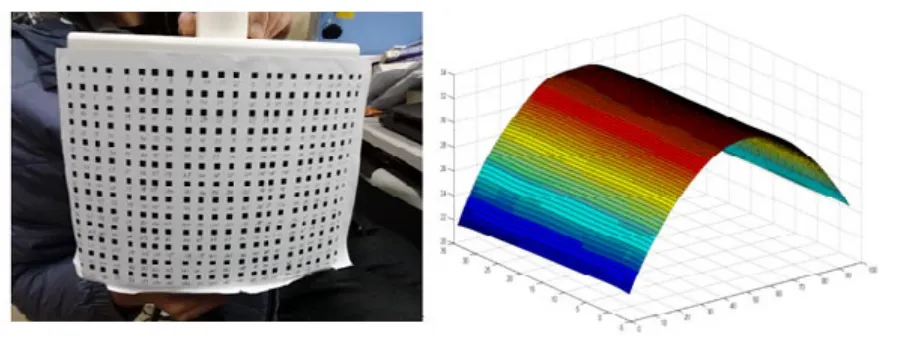
图5 任取弧面和重建弧面

为了验证精度，在这20个点中任意取7组相邻点，比如取：3、5、8、12、15、17、20这7个点，对任意两点间的x，y，z距离进行测量，与三维重建中的三维坐标得出的两点间的x，y，z坐标进行对比，得出以下表格：

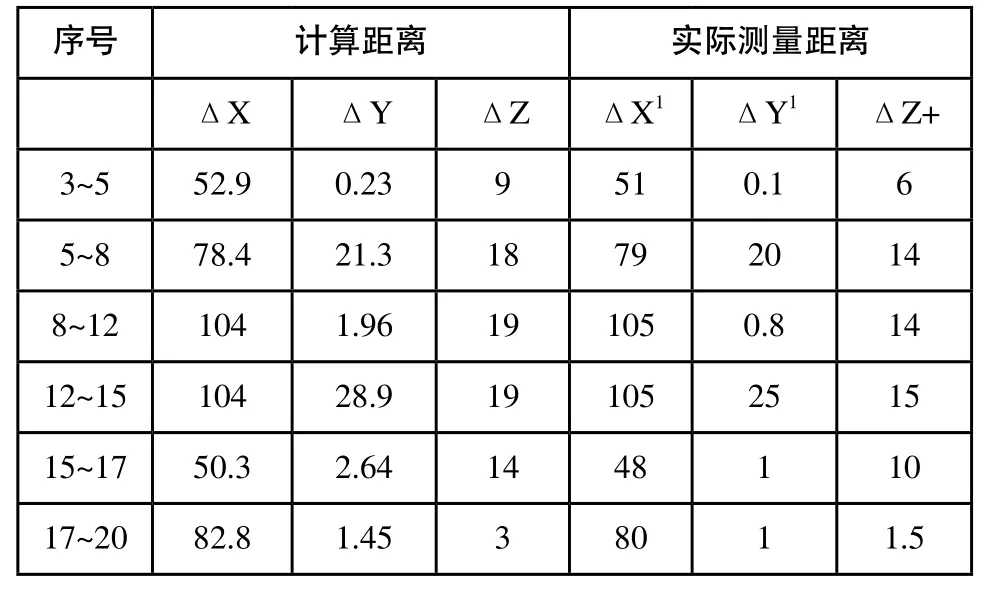
序号 计算距离 实际测量距离ΔX ΔY ΔZ ΔX1 ΔY1 ΔZ+3～5 52.9 0.23 9 51 0.1 6 5～8 78.4 21.3 18 79 20 14 8～12 104 1.96 19 105 0.8 14 12～15 104 28.9 19 105 25 15 15～17 50.3 2.64 14 48 1 10 17～20 82.8 1.45 3 80 1 1.5

可以看出，此方法得到的三维重建值存在一定的误差，其中可以看出x,y方向的重建精度高于z方向，z方向的三维重建值普遍大于实际测量值，整体数据满足项目的基本要求。

4 结束语

为了节约三维重建成本，提出基于特征点的三维重建方法。三维重建结果满足项目对三维重建的精度需求。

[1] 贾小军,等.编码结构光系统模型及误差分析[J].光学精密工程.2011(4).

[2] 战丽,刘国忠.用格雷编码结构光法测量三维面形[J].计算机测量与控制.2006(10).

[3] 王忠实,等.棋盘格模板角点的自动定位与识别[J].中国图像图形学报.2007,12(4).

[4] 梁锟.基于双目视觉的三维重建研究[D].2007.

[5] 张金苓.基于特征点和灰度相关的双目视觉匹配研究[D].2008.

[6] 张正友,马颂德.计算机视觉[M].北京:科学出版社,1998.

[7] http://www.vision.caltech.edu/bouguetj/calib_doc/.[EB/OL]