联合SVD在滚动轴承复合故障诊断中的应用

孟智慧，王 昌

MENG Zhi-hui,WANG Chang

（内蒙古科技大学 机械工程学院，包头 014010）

0 引言

滚动轴承作为机械设备中最常用的零部件之一，其运行状态直接影响到整台机器的性能。在工程实践中，滚动轴承的故障缺陷往往都不是单一的，常常同时发生几种故障，形成复合故障。复合故障的特征分离和故障识别是故障诊断领域中一大难点，亦是一个亟待解决的问题[1]。

奇异值分解[2]（Singular value decomposition,SVD）主要用于信号降噪处理及周期成分的提取[3]，在机电设备振动信号处理和故障诊断领域已有应用[4]。对于一维信号进行SVD处理时要首先将信号构造为矩阵的形式[5]，一般包括对信号连续截断方式构造的矩阵和重构吸引子矩阵，为此赵学智对不同构造形式矩阵的SVD分解进行了研究，提出的多分辨SVD[6,7]可以获得不同分辨率的近似和细节信号，在奇异性检测和消噪方面都有一定优势，此外还有微弱特征提取的能力；同时利用SVD差分谱[8,9]可以自动的判定SVD分解有效分量的个数，保留了信号中有用成分，同时又最大限度的消除了噪声。

本文提出基于多分辨SVD分解和SVD差分谱消噪的联合SVD的故障诊断方法，首先利用多分辨SVD将复合故障信号进行分解，然后再利用SVD差分谱对其进行降噪，即可实现复合故障的特征信息分离和提取。通过对滚动轴承内外圈复合故障信号的分析表明，该方法可以有效地分离和提取故障特征信息。

1 多分辨SVD

实矩阵A∈Rm×n,不论其行列是否相关，必定存在一对正交矩阵U=∈Rm×m和一个正交矩阵V=∈Rn×n，使得：

其中S=(diag(ó1,ó2,......óq),0)或者其转置，这取决于m＜n还是m＞n，其中，A ∈Sm×n，0代表零矩阵，q=min(m,n),ó1≥ ó2≥......óq≥0,0,它们称为矩阵A的奇异值。

借鉴小波多分辨分解的研究思想，利用SVD方法来获得信号在不同层次空间、具有不同分辨率的分解结果，从而实现类似于小波分析那样的可将信号分解到一系列不同层次子空间的多分辨率分解，称为多分辨SVD分解[7]。

进行SVD分解时首先要将一维信号序列构造成矩阵的形式，欲实现信号的多分辨率SVD分解，矩阵的构造采用了二分递推构造思想，即对信号序列Y=(y (1),y (2),......,y(N))按如下方式构造矩阵

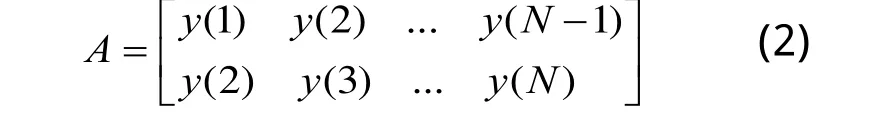
矩阵经过SVD处理后，产生两个奇异值，第一个奇异值较大，第二个奇异值较小，由此得到的信号分量对原始信号的贡献量也有轻重之分。多分辨SVD的主要思想是先分离出对原始信号贡献较小的分量，类似于小波分解时的细节信号（称其为SVD细节信号，记为Dj），对原始信号贡献较大的分量类似小波分解的近似信号（称其为SVD近似信号，记为Aj），再对Aj继续取行数为2构造矩阵进行下一层的SVD分解，逐次递推，将原始信号分解为一系列SVD细节信号和近似信号，设原始信号为A0，其递推SVD分解过程如图1所示。

多分辨SVD可实现对信号的多层次分解，这种分解方法矩阵结构简单，计算量较小，不存在矩阵行数和列数选择的难题。同时每次分解过程中分量始终为2个，不会造成能量的泄漏，即可将原信号的细节特征和主体信号以多层次展现出来，最后通过逆运算将一系列分解所得SVD近似及细节信号重构出来。

图1 信号二分递推SVD分解过程

2 SVD差分谱

利用SVD对信号降噪，往往将信号构造为Hankel矩阵，此时降噪效果最好[8]，离散数字信号构造形式为：

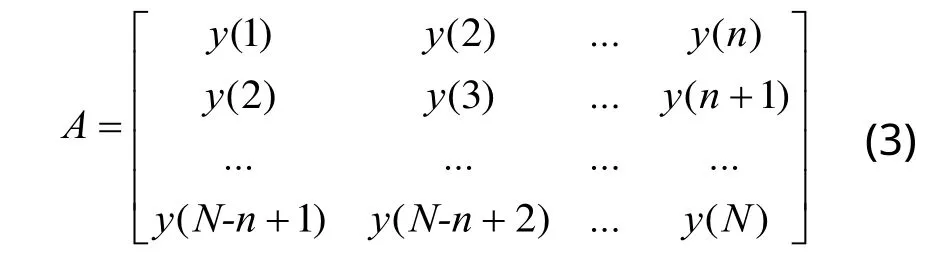
式中1＜n＜N。令m=N-n +1，则A∈Rm×n，上述矩阵称为重构吸引子轨道矩阵。为实现对信号各成分的充分分离，要求Hankel矩阵的行数和列数尽可能达到最大，故n=N/2，m=N/2+1。

对于SVD分解后的奇异值，按照从大到小的顺序形成的序列为：

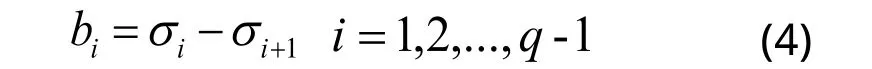
bi组成的序列称为奇异值的差分谱，含噪信号构造的Hankel 矩阵奇异值分解后，后面的q-k个奇异值明显小于前k个奇异值，也就是说奇异值在第k个点发生突变，而前k个奇异值代表了要提取的理想信号。由于每一个奇异值对应着一个分量信号，因此，只要选择前面k个分量进行简单的叠加，就可获得降低了噪声的信号，而差分谱就可以有效的自动判断最大突变点bk。

3 复合故障试验分析

试验系统由轴承试验台、压电式加速度传感器（美国PCB公司生产的627A61型ICP加速度传感器）、数据采集仪（杭州亿恒科技有限公司的MI6008型数据采集分析仪）、笔记本电脑组成。故障试验台如图2所示，将正常和有故障轴承依次安装在轴承试验台上，进行试验数据采集，将采集数据传到电脑中，进行数据处理分析。

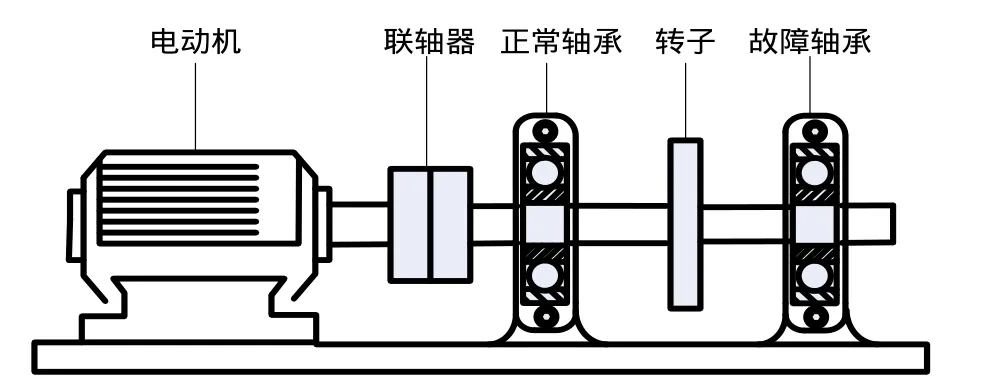
图2 滚动轴承故障试验台

该试验的滚动轴承型号为6307，电机转速为1496r/min，采样频率为15360Hz，采样点数是4096。利用线切割技术在轴承内外圈各加工了一条宽为0.5mm，深为0.5mm的槽来模拟裂纹故障，从而形成复合故障，将故障轴承安装在试验台末端轴承座上，加速度传感器垂直安装在末端轴承座上。经计算，内圈特征频率为122.738Hz，外圈的特征频率为76.728Hz。

图3为滚动轴承内圈裂纹和外圈裂纹复合故障信号的原始时域波形及希尔伯特包络解调谱，从波形图中可以看出信号有一定的冲击，在希尔伯特包络解调谱中，虽然可以找到75Hz和123.8Hz的频率成分，但有强烈的干扰成分。将原始信号进行4层多分辨SVD分解得到5个分量的波形如图4所示。

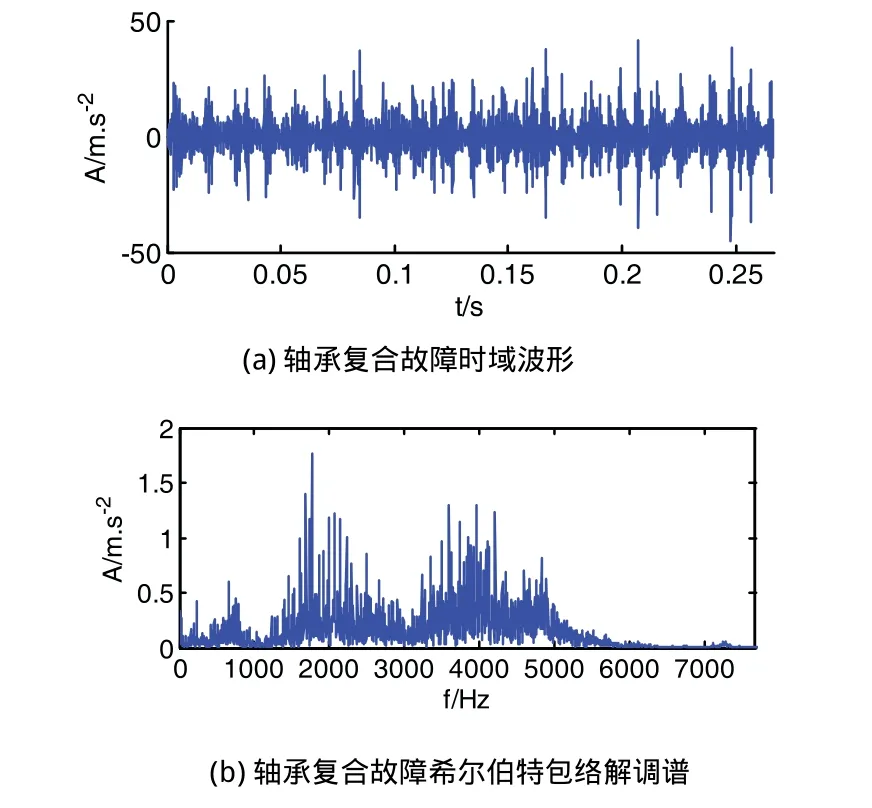
图3 轴承复合故障时域波形和希尔伯特包络解调谱

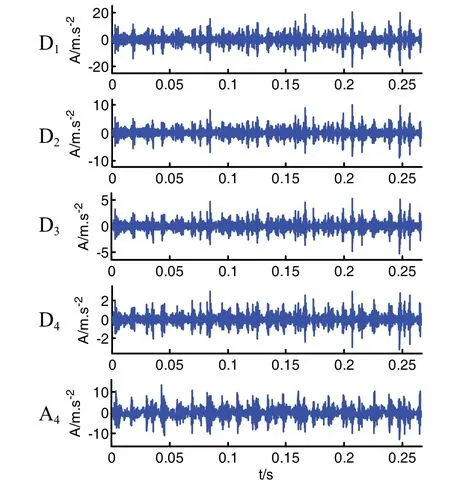
图4 4层多分辨SVD分解

对D2分量构造Hankel矩阵并进行SVD分解，求其差分谱曲线如图5所示，由于奇异值差分谱曲线的最大突变点在前段部分，后面的都趋于0。故只画出前100个点的曲线。可以清楚的看到在第6个点出现了最大突变，故保留前6个奇异值，其余的置为0进行SVD重构，即可得到降噪后的信号波形如图6所示，可以看到明显的周期性冲击，图7所示为降噪后的希尔伯特包络解调谱，在图中可以清楚的看到123.8Hz、243.8Hz...等频率成分，与轴承内圈的特征频率122.738Hz及其倍频非常接近，故可判断滚动轴承存在内圈故障。

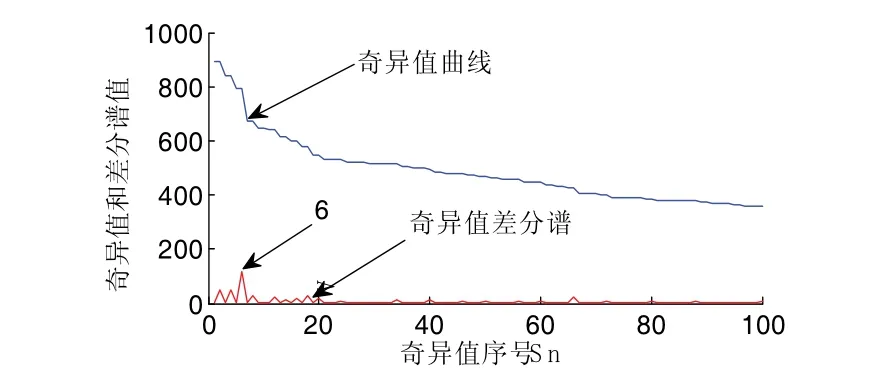
图5 D2分量的奇异值差分谱曲线

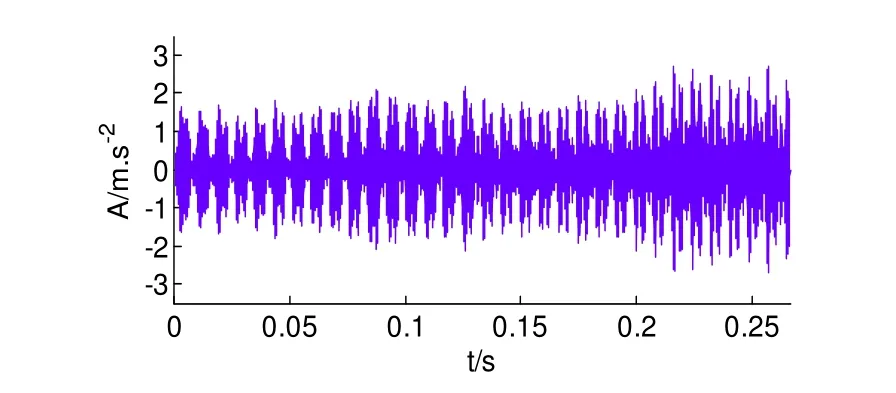
图6 D2分量的奇异值差分谱降噪后的波形

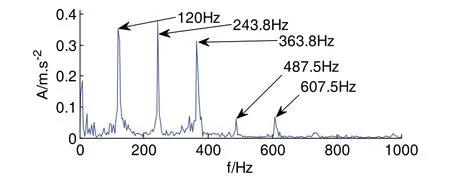
图7 D2分量降噪后的希尔伯特包络解调谱

同样，图8所示为A4分量构造Hankel矩阵后进行SVD分解所求差分谱曲线，最大突变点为4，保留前4个奇异值进行重构得到降噪后的波形如图9所示，对应的希尔伯特包络解调谱如图10所示。同样图中可以清楚的看到75Hz、153.8Hz...等频率成分，这与轴承外圈的特征频率76.728Hz及其倍频非常接近，故可判断该轴承外圈存在故障。上述结果表明，联合SVD的复合故障诊断方法可以有效地分离和提取复合故障特征信息。

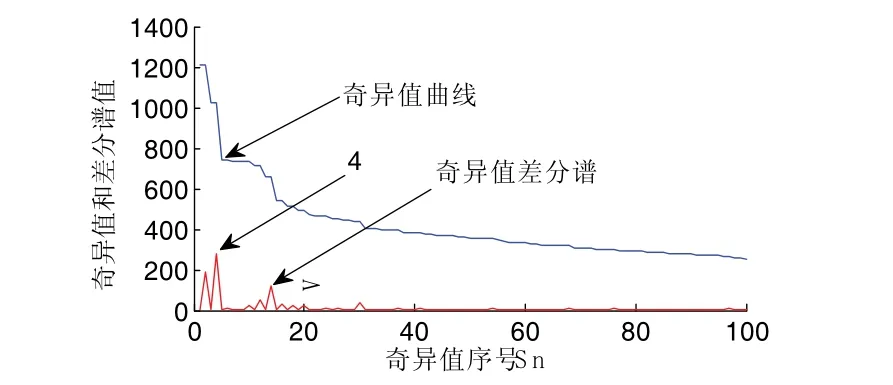
图8 A4分量的奇异值差分谱曲线

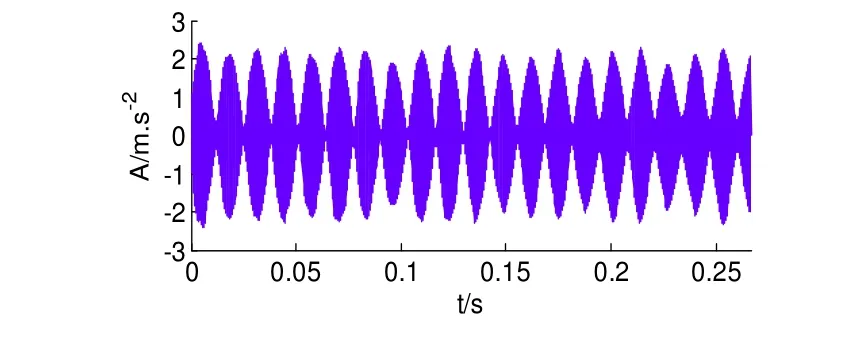
图9 A4分量的奇异值差分谱降噪后的波形

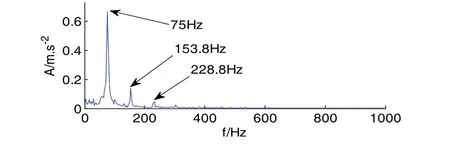
图10 A4分量降噪后的希尔伯特包络解调谱

4 结论

本文研究了将多分辨SVD分解和SVD差分谱降噪结合的联合SVD复合故障诊断方法，通过对滚动轴承内圈、外圈裂纹的复合故障试验分析表明。该方法可以有效地分离轴承复合故障的特征频率。

1）鉴于小波变换的思想，利用多分辨SVD的方法可以将信号分解为近似信号和细节信号，可用来分离信号。

2）利用SVD可以对含噪声振动信号进行有效降噪，而差分谱在降噪时可以自动确定SVD重构时有效奇异值的个数。

3）将多分辨SVD分解和SVD差分谱降噪结合的联合SVD故障诊断方法应用于复合故障诊断中，可以有效地分离和提取滚动轴承复合故障特征信息。

[1] 王晓冬,何正嘉,訾艳阳.多小波自适应构造方法及滚动轴承复合故障诊断研究[J].振动工程学报,2010,23(4):438-443.

[2] AKRITAS A G,MALASCHONOK G I. Applications of singular value decomposition (SVD)[J]. Mathematics and Computers in Simulation,2004,67(1):15-31.

[3] 吕志民,张武军,徐金梧.基于奇异谱的降噪方法及其在故障诊断技术中的应用[J].机械工程学报,1999,35(3):85-88.

[4] 李建,刘红星,屈梁生.探测信号中周期性冲击分量的奇异值分解技术[J].振动工程学报,2002,15(4):415- 418.

[5] 赵学智,叶邦彦,陈统坚.矩阵构造对奇异值分解信号处理效果的影响[J].华南理工大学学报,2008,36(9): 86-93.

[6] Xuezhi Zhao,Bangyan Ye. Similarity of signal processing effect between Hankel matrix-based SVD and wavelet transform and its mechanism analysis[J]. Mechanical Systems and Signal Processing,2009,23(4):1062-1075.

[7] 赵学智,叶邦彦,陈统坚.多分辨奇异值分解理论及其在信号处理和故障诊断中的应用[J].机械工程学报,2010,46(20):64-75.

[8] 赵学智,叶邦彦,陈统坚.基于小波—奇异值分解差分谱的弱故障特征提取方法[J].机械工程学报,2012,48(7):37-47.

[9] 赵学智,叶邦彦,陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J].机械工程学报,2010,46(1):100-108.